曲线趋势外推延伸方法研究及其应用

吴修彬，孙召瑞，孙贵斌，李国平,2

（1.莱芜职业技术学院 机械与汽车工程系，莱芜 271199；2.莱芜市粉末冶金先进制造重点实验室，莱芜 271199）

0 引言

箱体等铸造类零件常有过渡非圆曲线，针对其进行工程制图或三维建模，常需将非圆曲线保持其趋势进行延伸[1]。现有计算机辅助设计软件，如AutoCAD、Pro/E、UG等均有延伸功能。然而，除AutoCAD可延伸椭圆曲线外，现有软件仅对直线和圆弧能保持原有曲线特性进行延伸，对任意的非圆曲线或者不响应，或者改变原有特性进行延伸，如CAXA对任何曲线均以直线特性延伸。非圆曲线保持特性延伸是制图和建模中经常遇到的难题，实际应用中，只能采用手工绘制样条曲线进行替代，误差较大。

趋势外推法[2]是根据过去和现在的发展趋势推断未来的一类方法的总称，目前用于科技、经济和社会发展的预测[3～5]。如将趋势外推法的时间和数值视为曲线的坐标值，则可将其应用于非圆曲线的延伸。本文基于上述思想，在极角坐标系中研究任意非圆曲线趋势外推延伸方法，首先建立几种典型延伸数学模型，给出模型应用条件，供延伸具体曲线时采用，克服现有CAD软件共性关键难题。

1 多项式延伸模型

1.1 二次曲线模型

用最小二乘法[8]确定延伸参数。由式（1）得：

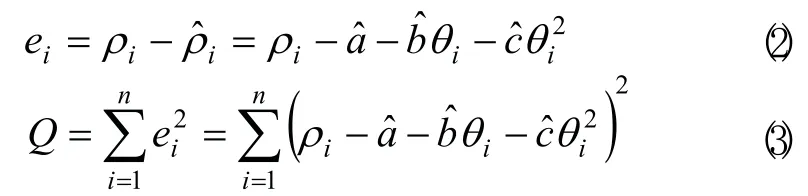
式中： r i为第i点的观察值； ei为第i点的离差；Q为离差平方和。

qi表示极角序列的编号，当极角序列观察点的项数为奇数时，令其中间项 的编号为0，

式（4）可简化为：

解方程组可得：

根据离散点数据采用式（6）计算延伸参数，依据式（1）建立延伸模型。

1.2 三次曲线模型

用最小二乘法确定延伸参数。由式（7）得：

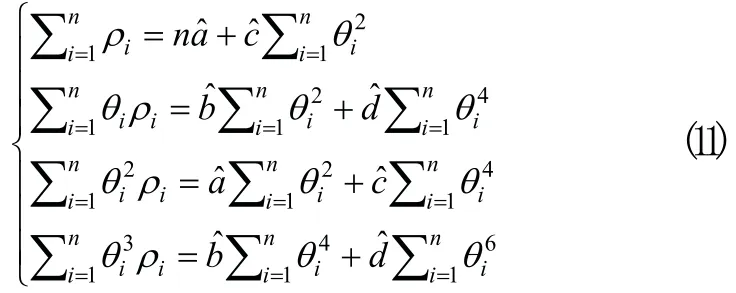
解方程组可得：

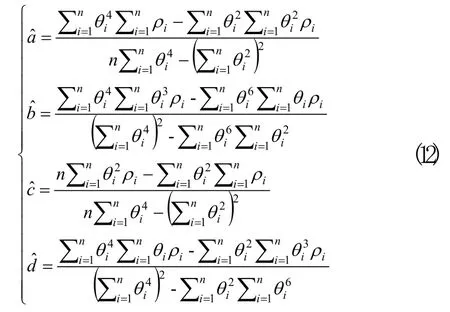
根据离散点数据采用式（12）计算延伸参数，依据式（7）建立延伸模型。

2 Gompertz曲线延伸模型

选N=3n组离散点，其中n是离散点分成3组后，各组离散点的个数。若N不等于3n，摒弃离延伸位置较远的若干点，使N=3n。将离散点代入下式：

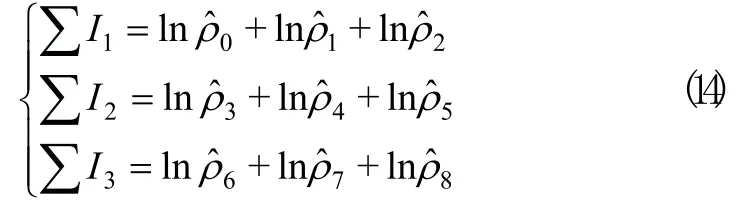
将有关数据代入下式，计算Gompertz模型所需参数。

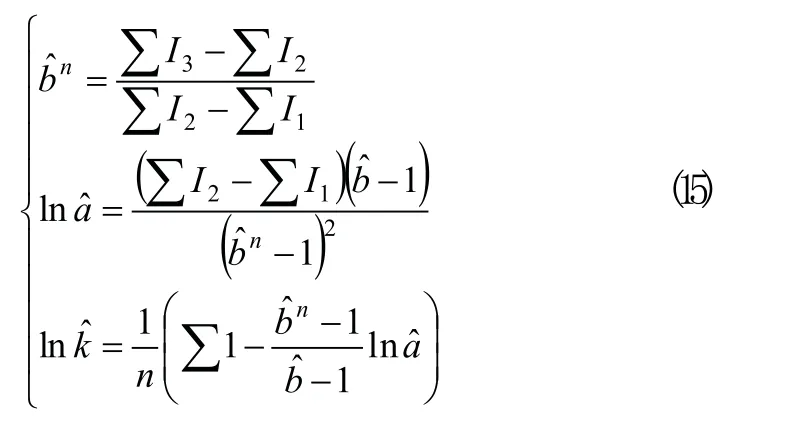
3 指数曲线延伸模型

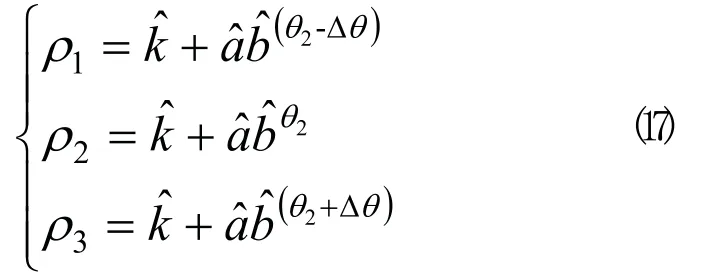
根据式（2）联立求得：

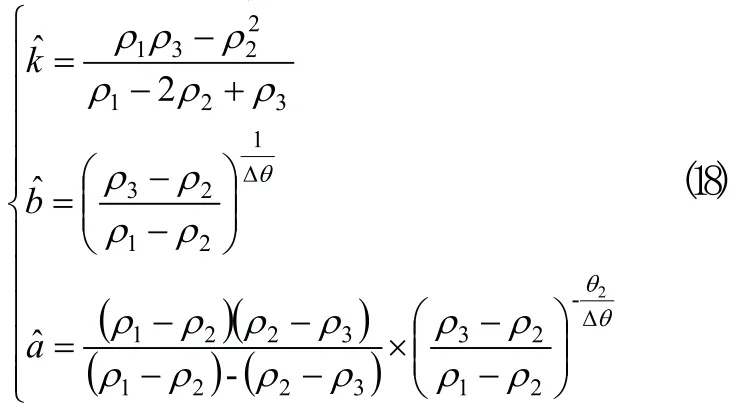
4 曲线趋势外推延伸实例

如表1所示，分别为二次曲线、三次曲线、Gompertz曲线、指数曲线上的4组离散点。应用上述方法对4条曲线进行延伸，分析延伸曲线与理论曲线间的误差，检验延伸模型的准确性。

表1 趋势外推延伸曲线离散点

分别拟合上述4组离散点，在拟合曲线上选取qi为等差数列的新离散点，分别计算4组新离散点延伸模型应用条件，如表2所示，曲线1的 最大差值最小，接近于常数，选用二次曲线趋势外推延伸模型；曲线2的 最大差值最小，选用三次曲线趋势外推延伸模型；曲线3的(▽l n ρi+1-▽lnρi)▽lnρi最 大 差 值 最 小 ， 选 用Gompertz曲线趋势外推延伸模型；曲线4的▽ln ρi最大差值最小，选用指数曲线趋势外推延伸模型。

对曲线1，经运算，延伸参数为： a ˆ=3.000+5.526×10-13， bˆ = 2.000+3.971×10-10，cˆ= 1.000+1.982×10-11。将（3.500，22.250）作为起始点，利用模型式（1）对曲线进行延伸，图1为延伸图及与理论曲线误差图，延伸误差在10-11数量级，精度较高。

表2 趋势外推延伸模型选择

图1 曲线1的延伸图及误差图

图2 曲线2的延伸图及误差图

图3 曲线3的延伸图及误差图

图4 曲线4的延伸图及误差图

5 结论

1)引入趋势外推方法，建立多项式、Gompertz曲线、指数曲线3类延伸数学模型，提供了模型识别与选择方法，根据待延伸曲线离散点特征可合理选择延伸模型，实现非圆曲线趋势外推延伸。

2)曲线趋势外推延伸实例表明：用所建立的延伸模型延伸与之同类型的曲线，可以长距离延伸，精度非常高，且距延伸起始点越近，精度越高，达到趋势外推延伸。对与延伸模型不同类型的曲线，也可近似延伸。

3)曲线趋势外推延伸方法可应用于对现有CAD软件的核心升级，也可对其进行二次开发，增加其功能模块，使之更精确的进行交互式设计。

[1] 刘有余,韩江.基于减容增效的超低比转速轴流式叶片水力设计[J].中国机械工程,2012,23(3):320-323.

[2] V.M. Vlahović, I.M.Vujošević. Long-term forecasting:a critical review of direct-trend extrapolation methods[J]. International Journal of Electrical Power & Energy Systems.1987,9(1):2-8.

[3] M. D. Ruiz-Medina,R.M.Espejo.Integration of spatial functional interaction in the extrapolation of ocean surface temperature anomalies due to global warming [J].International Journal of Applied Earth Observation and Geoinformation,2013,22(6):27-39.

[4] Gosse L.Analysis and short-time extrapolation of stock market indexes through projection onto discrete wavelet subspaces [J]. Nonlinear Analysis: Real World Applications.2010,11(4):3139-3154.

[5] 杨立群,王小万,冯芮华.基于指数平滑方法的我国政府卫生支出分析[J].中国卫生经济,2011,30(1): 22-23.

[6] 陶菊春. 趋势外推预测模型的识别与选择研究[J].西北师范大学学报(自然科学版).2005,41(6):14-17.

[7] Vladimir D L. Grid Generation Methods [M]. London:Scientific Computation,2010.

[8] 崔静伟,雷贤卿,王海洋,等.基于最小二乘法的平面任意位置椭圆轮廓度误差的精确计算[J].制造业自动化.2013, 25(2):114-116.

[9] Hu G X. Invariant distribution of stochastic Gompertz equation under regime switching[J]. Mathematics and Computers in Simulation.2014,97(3):192-206.

[10] A. B. Albert, On Exponential Growth and Half-Lives: A Comment on Bermingham, Population & Environment[J].Population and Environment,2003,25(1),61-69.