基于DBNs的反导态势评估模型研究*

林傲，肖兵，朱艺

(空军预警学院 a.研究生管理大队；b.四系，湖北 武汉 430019)

0 引言

现代战场信息化程度高，战场环境日趋复杂，如何有效融合战场信息，并为指挥员指挥作战提供决策支持，对于取得战争胜利越来越重要。弹道导弹作为一种远程精确打击的有效武器，在现代战场中发挥越来越重要的作用[1]。对于反导作战而言，战场在空间上跨度较大，在时间上持续时间短，同时多目标进攻使得弹道导弹的拦截更加困难[2]，为反导指挥作战提出了严峻的挑战。因此，指挥员必须依靠及时准确的战场态势评估信息，作出及时正确的决策。

国内外对态势评估已经展开了大量研究，贝叶斯网络也作为一种成熟的不确定性推理方法被成功应用在态势评估中[3-5]。但是，一方面由于静态贝叶斯网络没有考虑前后时刻的态势信息的关联和相互影响，不能适合战场态势的连续性变化；另一方面，由于来袭导弹的数量对反导战场态势影响巨大，当多枚导弹进攻时，固定不变的态势模型不能满足态势评估要求。因此，本文借助于模块化[6]和变结构贝叶斯网络[7]思想，依据多导弹攻击下的战场特点，提出了一个反导战场全局态势评估动态贝叶斯网络(dynamic Bayesian networks,DBNs)模型。该模型能够根据来袭导弹的数目调节态势评估模型结构，同时根据时间变化动态推理态势结果，使得模型能更加真实描述战场态势。

1 多导弹攻击下的态势评估DBNs模型分析

文献[8]给出了单枚弹道导弹态势评估模型，多导弹态势评估可以以此为基础，把单枚导弹态势评估模型模块化并作为多导弹态势评估模型节点，有多少进攻导弹就有多少个单导弹态势评估模型节点，进而借助于动态贝叶斯网络推理得到全局战场态势，使得态势结果不是单导弹的态势评估简单叠加得到，更适合战场实际。

1.1 单枚导弹贝叶斯网络模块

弹道导弹作为一种精确打击武器，每一枚导弹的欲打击目标以及打击效果，即导弹的攻击意图(G)，在导弹发射之初就已经确定，因此，导弹的攻击意图对战场态势发展有着重要影响。防御方可以通过综合观测导弹飞行中的特征以及通过技术侦察得到的目标情报，推理得到单枚导弹的攻击意图。单枚导弹贝叶斯网络如图1所示，其中各个节点的状态根据不同战场的情景和决策需求设定。比如某战场反导方有n个重要目标，按照目标的重要性从大到小排序，那么导弹的目标意图、落点预报[9]以及导弹距离的状态就是{M1，M2，…，Mn}，落点预报是指导弹的重力学飞行弹道终点距离目标点的距离远近，导弹距离指的是导弹距离目标点距离的远近，越近的目标点该状态值越高；导弹速度状态有{极快，快，中}3种，分别表征导弹飞行中的速度快慢；导弹突防[10]状态有{多，少，无}3种，分别表征导弹作战过程中的突防动作的多少；弹头类型状态有{T1，T2，T3}3种，分别对应于多弹头、子母弹和单弹头3种常见的弹头类型[2]；攻击意图状态有{摧毁重要目标(CZ)，摧毁一般目标(CY)，破坏或扰袭(PR)}3种。

图1 单枚导弹BN模块Fig.1 BN module of individual missile

根据图1所示的模块中变量间的连接关系相对固定，而在不同来袭导弹数量的条件下，单枚导弹模块内部的参数关系以及攻击意图转移概率也可以简化为固定不变。同时为了研究方便，导弹意图、落点预报和导弹距离的状态确定为{M1,M2,M3}3种，对于不同的导弹，M1～M3可以指不同的具体目标，按照重要性M1>M2>M3。

在确定了节点关系之后，接下来需要分配节点概率。节点概率包括先验概率和条件概率。条件概率可以通过样本学习或通过专家经验估计确定，当缺少样本建模时，节点概率通常由领域内的专家根据经验指定，从而使得贝叶斯网络模型从一开始就包含了相关的领域知识[11]。由于缺乏样本数据，本文对网络参数通过专家经验来估计。

专家结合经验知识，按照因果关系对网络参数进行估计。比如，假设敌方攻击意图为摧毁重要目标时，专家估计导弹会攻击M1，M2和M3的概率分别为0.6，0.2和0.2，其他节点的概率用同样的方法确定。最终确定G隐藏节点的先验概率为{0.3,0.4,0.3}，同时确定单枚导弹BN(Bayesian network)模块节点的条件概率，如表1～3所示。

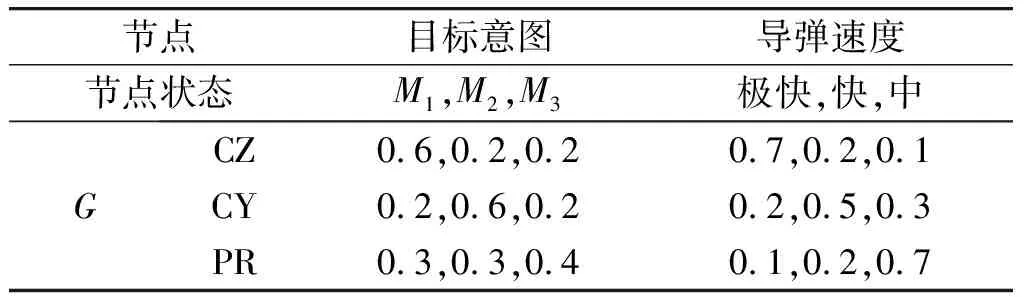
表1 目标意图和导弹速度节点的条件概率Table 1 Conditional probability of the objective intent and speed of missile nodes

表2 落点预报和导弹距离节点的条件概率Table 2 Conditional probability of landing prediction and distance of missile

表3 弹头类型和导弹突防节点的条件概率Table 3 Conditional probability of warhead type and missile penetration nodes

1.2 反导战场全局态势评估DBNs

反导战场全局态势指的是在空间上和时间上全面描述反导战场的态势。“空间”主要指能够全面描述作战双方的兵力变化情况，在反导战场中主要指的是来袭导弹的数量变化和防御方的拦截情况。“时间”主要指战场态势能随着时间变化，动态推理战场态势。本文根据全局态势评估要求，假设全局态势只受来袭导弹与来袭导弹的作战效果影响，提出了变结构的态势评估DBNs模型，随时间变化的模型结构如图2所示。对全局态势分了4个等级，分别对应{Ⅲ,Ⅱ,Ⅰ,0}，等级越高，则战场形势越严峻，指挥员可以据此把握全局态势并作出决策。

一枚导弹在作战中有2个阶段，前一个阶段是在飞行中，可以通过对导弹的观测证据推理导弹的攻击意图；后一个阶段为导弹结束飞行阶段，通过对导弹攻击效果的实时事后分析得到。全局态势中，第1阶段来袭导弹节点用单枚导弹BN模块表示，有多少来袭导弹就对应多少个模块，假设一次作战中，共有m枚来袭导弹，则Gi(i=1,2，…,m)。第2阶段中，虽然模块中的观测节点没有了数据来源，但是导弹的作战效果同样会对全局态势有不同的影响。假如防御方对来袭导弹拦截失败，导弹摧毁了防御方重要目标，那么会导致战场态势向更恶劣的方向发展；而当拦截成功，该枚导弹对战场目标的威胁大大降低，对战场态势影响较小，从而影响指挥员指挥决策。导弹的真实作战效果可以通过对战场的实时事后评估得到。事后评估用S表示，共有m枚来袭导弹，则Si(i=1,2，…,m)。S为观测变量，有{摧毁重要目标(ZY)，摧毁一般目标(YB)，拦截成功(LJ)}3种状态。当S一旦确定，其数值就不再随时间变化。该模型中共有全局态势、攻击意图和目标意图3个隐藏变量，为了简化模型的推理，只选取战场态势、攻击意图2个变量作为动态变量，动态变量对后一个时刻的推理有影响，而其他隐藏变量只对当前时刻的推理有影响。根据单枚导弹BN模块，模型的观测变量有导弹落点、导弹距离、导弹速度、导弹突防和弹头类型，此外，对导弹攻击效果的事后评估也是观测变量。

全局态势评估DBNs如图2所示，全局态势变量用Q表示。当观测到有来袭导弹时，态势评估开始，到第k时刻，第2枚导弹来袭，到第l时刻，第i枚导弹来袭，直到第p时刻，所有导弹都结束飞行，态势评估结束。

图2 全局态势评估DBNsFig.2 Global situation assessment DBNs

根据全局态势评估DBNs，战场态势变量的子节点是可变的，主要体现在单枚导弹模块的个数变化和模块转变为事后评估2个方面的变化上。由于子节点的状态相同，可以认为全局态势评估DBNs节点的条件概率在评估过程中是稳定不变的，如表4所示。

根据专家知识，确定全局态势节点的先验概率为{0.2,0.3,0.3,0.2}，同时确定全局态势和G的状态转移概率，如表5所示。

表4 G和S节点的条件概率Table 4 Conditional probability of G and S nodes

表5 全局态势和G节点的转移概率Table 5 Transition probability of global situation and G nodes

2 变结构DBNs推理算法

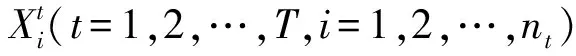
2，…,mt)。前后2个时间片间的状态转移概率表为InterCPTt。对DBNs的推理就是计算隐藏节点在所有观测变量在某一观测状态组合下的联合分布，同时根据贝叶斯条件独立性以及贝叶斯公式(式(1))，推导可得联合分布，如式(2)所示。

(1)

(2)

(3)

结合式(3)输入T个时间片的观测变量软证据信息，就可以得到隐藏变量的所有状态组合联合分布。由于时间片T的选择决定式(3)的计算量，而反导作战态势评估对实时性要求高，因此在本文中选择T=1个时间片。

3 仿真分析

为了简化战场想定，假定某一战场发现有3枚导弹来袭，3枚导弹的飞行参数相同，导弹每隔5 min发射一枚。这3枚来袭导弹为射程4 000 km左右的中程弹道导弹，总飞行时间为20 min左右。第1枚的来袭导弹部分观测值(不包括事后评估)如表6所示，其他2枚的观测值，除时间相应增加300 s和600 s以外，后续2枚导弹的观测值和第1枚观测值相同。

为比较模型描述战场态势变化的能力，假定2种战斗情景：一是3枚导弹均没有被拦截成功，并达到了摧毁重要目标的效果，事后评估S1，S2和S3证据均为{0.9,0.1,0}；二是第1枚导弹拦截失败，摧毁了重要目标，事后评估S1证据为{0.9,0.1,0}，第2枚和第3枚导弹被防御方成功拦截，事后评估S2和S3证据均为{0,0.1,0.9}。

为对比全局DBNs模型，分别构建了全局BN模型和单导弹DBNs模型。全局BN模型与全局DBNs模型相比，前者没有设定动态节点。单导弹BNs模型是在单枚导弹BN模块的基础上，选择攻击意图为动态节点，网络参数和全局DBNs模型一致。

利用贝叶斯网络工具箱和Matlab 7.1软件，在计算机上加装数据和推理算法并运行。分别对单导弹DBNs模型、全局DBNs模型和全局BN模型的2种战斗情景进行仿真，由于在单导弹DBNs模型仿真中每一个导弹就有一个评估结果，因此对3枚导弹的态势结果进行平均。提取6次仿真各10个时刻的态势评估推理结果，如图3所示。

从图3中可以看出，由于单导弹DBNs模型没有考虑到事后评估对态势的影响，2种战斗情景得出的态势结果是一样的，并且看不出战场的全局态势变化。在第1种战斗情景中，全局DBNs和全局BN模型均能反映出3枚导弹均没有被拦截成功的态势情况，但是全局DBNs模型对态势的变化更加敏感。具体体现在第1枚导弹发射时，在图3c)中态势状态“Ⅰ”超过0.5，其他状态未超过0.4；第2枚导弹发射后态势状态“Ⅱ”从前一个时刻的0.1左右增长到接近0.5，而状态“Ⅰ”降至0.1；第3枚导弹发射后态势状态“Ⅲ”从不到0.1迅速增至0.7，随着时间的增长，态势状态“Ⅲ”逐渐增加并稳定在0.8左右。而在图3e)中却看不出这种明显的变化，态势状态区分不明显，尤其是态势状态对导弹的数量不够敏感，当3枚导弹来袭后，最高等级态势状态“Ⅲ”上升不够迅速。在第2种战斗情景中，从图3d)和图3f)的后期变化中，全局DBNs模型也是优于全局BN模型的，前者能够体现出第2枚导弹被拦截后，态势状态“Ⅱ”增加迅速，状态“Ⅲ”下降明显的变化，能够体现出第3枚导弹被拦截后，态势状态“Ⅰ”增加迅速，而状态“Ⅱ”下降明显的变化。

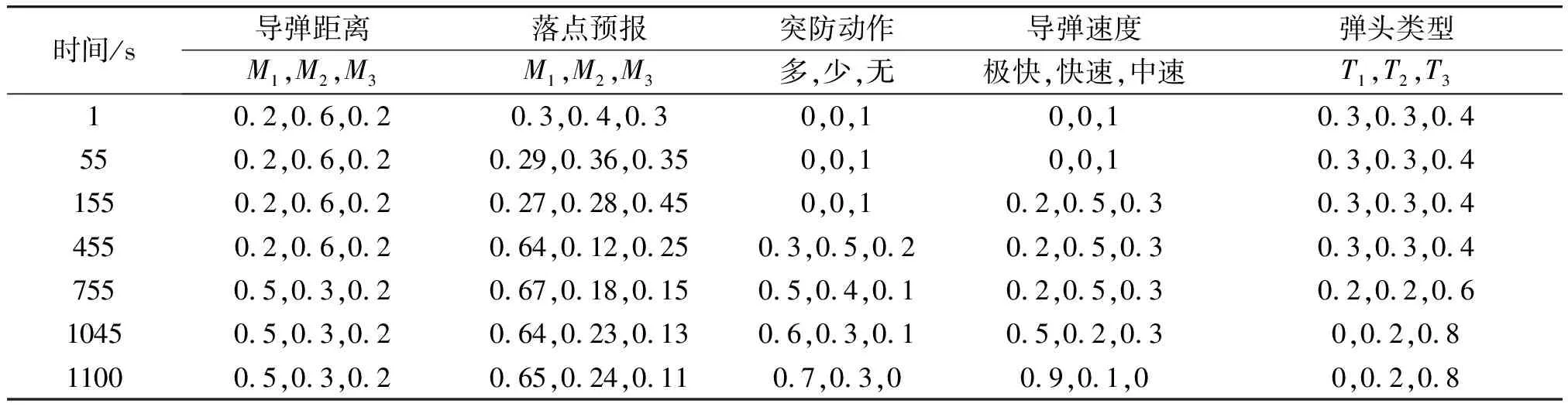
表6 部分观测值

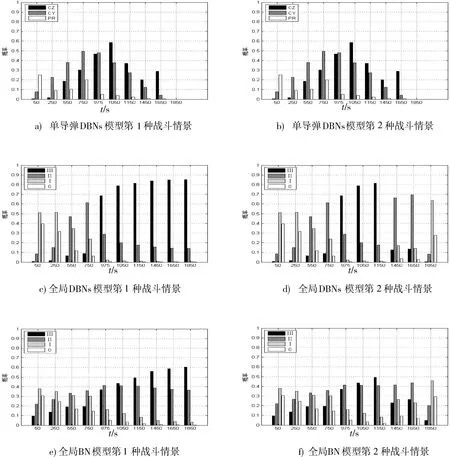
图3 态势评估推理结果Fig.3 Reasoning result of situation assessment

因此，全局DBNs模型推理结果能够更加准确地描述复杂情景的变化，这主要是由于在空间上，全局DBNs模型能够考虑多枚导弹的综合影响；在时间上，全局DBNs模型能考虑前后时刻的态势结果影响，可以滤除传感器的误差，从而保持评估过程的鲁棒性。

4 结束语

本文构建的全局DBNs态势评估模型，与单导弹DBNs态势评估模型和全局BN态势评估模型相比，更适用于反导战场态势的变化，尤其是对导弹的数量变化和导弹拦截的成功与否等重要事件，前者的态势等级变化更加准确和显著。全局DBNs态势评估模型的基础是单枚导弹态势评估模型模块，来袭导弹的数目决定模块的数目，导弹飞行结束后，用导弹对目标真正打击情况的事后评估替代模块推理结果，这样能更加真实地反映态势变化和真实情况。由于战场过于复杂，在研究中作了不少理想化的假设和简化，下一步的研究中，要根据双方作战背景和战场实际，对模型节点的选取和状态的选择展开研究，进一步提高模型准确性。

参考文献：

[1] 朱华桥. 2020年前战略弹道导弹国际发展态势[J]. 中国航天，2012(9): 60-63.

ZHU Hua-qiao. The International Momentum of Development in Rategic Ballistic Missile before 2020[J]. Aerospace China， 2012(9): 60-63.

[2] 张洪波，汤国建. 弹道导弹防御中多目标拦截的策略[J]. 现代防御技术，2007, 35(2): 23-26.

ZHANG Hong-bo, TANG Guo-jian. The Tacticses of Multitarget Interception in Ballistic Missile Defense[J]. Modern Defence Technology,2007, 35(2): 23-26.

[3] MIRMOEINI F, KRISHNAMURTHY V. Reconfigurable Bayesian Networks for Adaptive Situation Assessment in Battlespace[C]∥Proceedings of 2005 IEEE on Networking, Sensing and Control, 2005:810-815.

[4] XIANG Yan-ping,ZENG Yi-feng,ZHU W, et al. An Intelligent Design System for Military Situation Assessment[C]∥Proceedings of 2008 3rd International Conference on Intelligent System and Knowledge Engineering，Xiamen,2008：158-163.

[5] ZHENG Tang, GAO Xiao-guang, ZHANG Ying. Overview of Research on Assessment Model of Radiant Threat Rank Based on Dynamic Bayesian Network[C]∥Proceedings of 2005 IEEE International Conference on Automation and Logistics,Jinan, 2007: 1067-1071.

[6] 田凤占，张宏伟，陆玉昌，等. 多模块贝叶斯网络中推理的简化[J]. 计算机研究与发展，2003, 40(8): 1230-1237.

TIAN Feng-zhan, ZHANG Hong-wei, LU Yu-chang, et al. Simplification of Inferences in Multiply Sectioned Bayesian Networks[J]. Journal of Computer Research and Development， 2003, 40(8): 1230-1237.

[7] 高晓光，陈海洋，史建国. 变结构动态贝叶斯网络的机制研究[J]. 自动化学报， 2011, 37(12): 1435-1444.

GAO Xiao-guang, CHEN Hai-yang, SHI Jian-guo.Study on the Mechanism of Structure-Variable Dynamic Bayesian Networks[J]. Acta Automatica Sinica， 2011, 37(12): 1435-1444.

[8] 林傲，肖兵，黄子俊，等. 一种变结构动态贝叶斯网络的反导态势评估模型[J]. 空军预警学院学报，2012, 27(2): 126-130.

LIN Ao, XIAO Bing, HUANG Zi-jun, et al. An Antimissile Situation Assessment Model Based on Variable Structure Dynamic Bayesian Network[J].Journal of Air Force Early Warning Academy，2012, 27(2): 126-130.

[9] 刘彦君，乔士东，黄金才，等. 一种高精度弹道导弹落点预测方法[J]. 弹道学报， 2012, 24(1): 22-26.

LIU Yan-jun, QIAO Shi-dong, HUANG Jin-cai, et al. A Method of Impact Point Prediction of Ballistic Missile[J]. Journal of Ballistics，2012, 24(1): 22-26.

[10] 汪民乐. 弹道导弹突防对策综述[J]. 飞航导弹，2012(10): 45-51.

WANG Min-le. The Summary to the Penetration Game of the Ballistic Missile[J]. Winged Missiles Journal， 2012(10): 45-51.

[11] DARWICHE A. Modeling and Resoning with Bayesian Networks[M]. New York: Cambridge University Press, 2009.

[12] CHEN Hai-yang, GAO Xiao-guang. Ship Recognition Based on Improved Forwards-Backwards Algorithm[C]∥ IEEE,Proceedings of 6th International Conference on Fuzzy Systems and Knowledge Discovery,China,Tianjin，2009:509-513.