基于摄动理论的落点预测算法研究*

田再克，杨锁昌，冯德龙，姚运志

(军械工程学院 导弹工程系，河北 石家庄 050003)

0 引言

脉冲弹道修正弹的基本原理是在弹丸质心附近布置多个脉冲发动机，通过脉冲发动机提供的侧向脉冲力，对弹丸的飞行轨迹进行快速修正。这种修正方法具有作用时间短、系统简单、成本低廉等特点，特别适用于常规弹药的制导化改造[1]。

本文讨论的弹道修正火箭弹采用GPS(global positioning system)导航，以地磁传感器作为滚转姿态测量元件。在弹丸发射后，弹载计算机通过导航卫星提供的实时位置和速度信息对落点进行预测，当预测落点与目标点存在较大偏差时，弹载计算机根据地磁传感器提供的弹丸姿态信息选择相应方位的脉冲发动机激活，改变弹丸飞行轨迹，实现弹道修正的目的[2]。

1 摄动制导系统设计

制导控制系统最重要的问题就是如何利用GPS实测的飞行弹道数据预测弹丸的无控落点。传统的通过求解外弹道微分方程(4D弹道) 的落点预测方法，计算复杂，实时性差，无法满足弹道修正制导系统的要求[3]。摄动方法是在弹道扰动很小的情况下用线性化函数逼近非线性函数的一种研究方法，弹道方程通常由一组运动微分方程组成，按照所给定的初始条件和实际飞行环境，可以计算出对应的标准弹道。按照摄动理论，实际弹道应在该标准弹道附近作小振幅的“摆动”，利用弹载GPS的实测数据与标准弹道的偏差可以实时预测弹道落点。摄动制导可充分利用线性函数的叠加性、放大性等特性，便于制导方程的分析和计算。由于脉冲力作用时间极短，可认为弹道是瞬时增加了一个速度矢量，对弹道的扰动很小，因此本文根据摄动理论设计弹道修正弹的制导系统[4]。

根据落点偏差设计的控制系统的设计如图1所示。

图1 弹道修正系统工作原理Fig.1 Schematic of trajectory correction system

2 脉冲发动机点火条件

由于脉冲修正控制方法不同于舵翼控制或推力矢量控制等连续控制方法，脉冲发动机点火条件通常包括以下4个方面[5-6]：

(1) 点火阈值

根据飞行控制器解算出的点火需求数应大于点火阈值，即

Ne>Nfire.

(1)

(2) 点火时间间隔

避免脉冲发动机激活过于频繁造成弹体的剧烈抖动，造成攻角过大而失稳，相邻2次点火间隔应大于点火时间间隔，即

t-t*>Δtfire.

(2)

(3) 脉冲发动机作用角度

为使脉冲发动机达到最大的修正效果，要求脉冲发动机作用角与弹道偏差相位角的差值在一定范围内，即

θ-α<Δδfire.

(3)

(4) 每个脉冲发动机只能激活一次

必须同时满足以上4个要求才能激活脉冲发动机对弹道进行修正。

3 基于多项式拟合的落点预测算法

弹道修正弹在被动段只受重力和飞行阻力的影响，其在横向受力比较简单，弹道近似直线，而在纵向其受力比较复杂，弹道类似二次曲线。因此本文以纵向落点预测为例介绍了一种适用于脉冲弹道修正弹的落点预测算法。并根据落点误差计算点火需求数，当需求数达到点火阀值时激活脉冲发动机进行弹道修正[7-8]。

修正弹全射程L对落点的偏差(包括射程偏差ΔL和横向偏差ΔH)是实际发射飞行条件的函数，建立射程与弹丸运动状态有关的函数：

L=f(x,y,z,vx,vy,vz).

(4)

根据摄动理论原理，实际射程在标准弹道附近展开，展开点可以选择沿标准弹道的所有点，对预测点进行展开得到射程预测方程为

L(tk)=L0+k1Δxk+k2Δyk+k3Δzk+k4Δvxk+

k5Δvyk+k6Δvzk,

(5)

即，剩余射程为

L′=L(tk)-xk，

(6)

式中：L(tk)为预测点预测射程；L0为理论射程；L′为剩余射程；Δxk，Δyk，Δzk，Δvxk，Δvyk，Δvzk为预测点坐标和速度的摄动量；偏导数ki等为射程偏差误差系数，其物理意义为单位运动参数偏差引起的落点偏差大小。

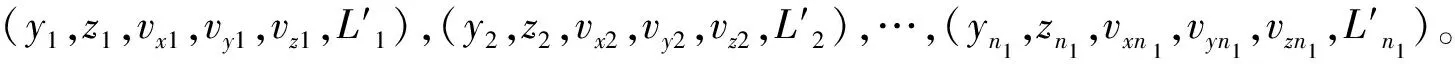
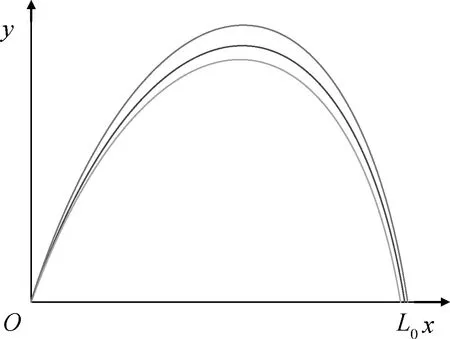
图2 弹道示意图 Fig.2 Schematic of ballistic

在一定情况下，多项式模型的阶数越高，模型越精确，越能反映L′与变量之间的非线性关系，但阶数越高测量误差对预测结果的准确性影响越大，影响射程预测的鲁棒性。经仿真分析，二阶模型的精度符合设计要求，因此本文采用二阶模型进行多项式回归运算。

引入矩阵符号：

(7)

k=(k0，k1，k2，…，k10)T，

则式(5)可写为

L′=Uk+e.

(8)

由最小二乘法可以得到回归系数的估计

k=(UTU)-1UTL′.

(9)

同时求得随机误差向量

e=L′-Uk.

(10)

当e服从高斯分布时，最小二乘估计为有效估计，则说明剩余射程预测模型是准确的，同理可解出横向落点预测模型。

利用Matlab仿真软件，在标准大气压下，对射程为28 km的弹道进行1 024次弹道仿真试验，验证预测算法精度。取每个弹丸飞行45 s时的预测落点与最终仿真试验落点进行比对，根据落点偏差考察落点预测精度。纵向落点预测精度如图3所示，横向落点预测精度如图4所示，仿真结果表明，横纵向预测落点精度达到5 m以内，该算法满足制导系统精度设计要求。

图3 纵向落点预测偏差 Fig.3 Vertical deviation of the impact point prediction

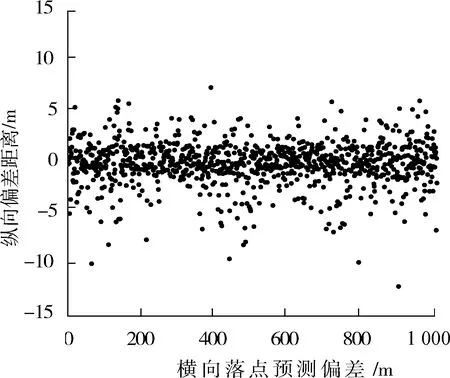
图4 横向落点预测偏差 Fig.4 Lateral deviation of the impact point prediction

4 点火需求数的计算

弹丸在飞行过程中受到脉冲修正力作用，使弹道倾角略微变化，相当于增加了一个速度矢量Δv，如图5所示[9]。

图5 速度增量示意图 Fig.5 Schematic of velocity increment

增加的速度矢量主要与脉冲发动机总冲量和弹丸质量有关，忽略其他次要因素，可得

Δv=I/m.

(11)

由Δv求取其在各个坐标轴上的分量需要知道脉冲发动机作用角度以及弹丸的俯仰姿态角。根据上文的算法，可以实时预测弹丸的落点，并计算横纵落点偏差。由横纵落点偏差ΔH,ΔL可以确定脉冲力作用角度θ，如图6所示。

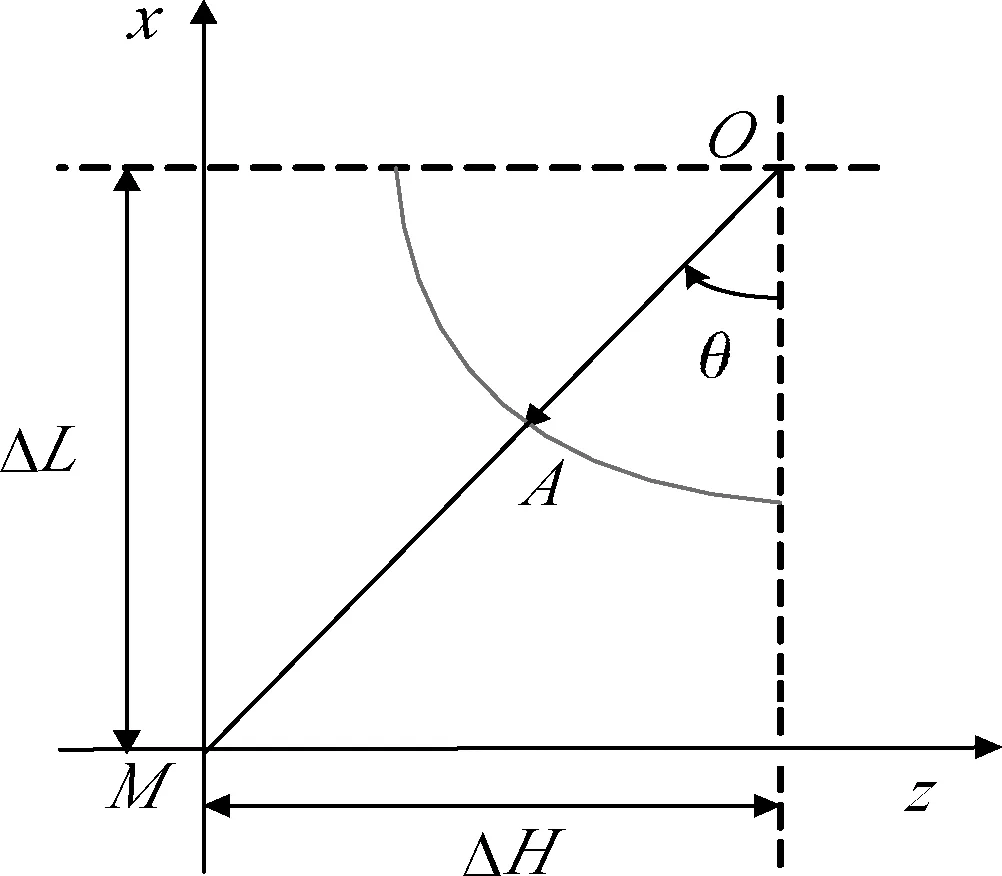
图6 脉冲力作用角度示意图 Fig.6 Schematic of pulse force angle

但弹丸的俯仰姿态角并不能直接求出，由于弹丸飞行比较稳定，飞行攻角小，可以用弹道倾角近似代替俯仰姿态角。弹道倾角φ可以由已知的速度信息求出，则Δv各方向上的分量可表示为

(12)

脉冲发动机作用时间极短，认为弹丸在瞬间获得速度矢量Δv，此时弹丸的位置不发生变化。因此，单个脉冲发动机作用后引起的射程变化为

f(x,y,z,vx,vy,vz)，

(13)

则纵向点火需求数为

(14)

同理可以求出横向点火需求数，进而求得总的点火需求数。

5 仿真及分析

基于Matlab软件建立6自由度弹道仿真模型，采用龙格-库塔法(Runge-Kutta)进行弹道仿真试验[10-12]。脉冲发动机工作参数为单脉冲发动机冲量15 N·s，总发动机个数40，多层结构，均匀地安装在弹丸的质心前侧，据弹丸质心为L，其构造布局及控制力如图7，弹丸转速15 r/s。

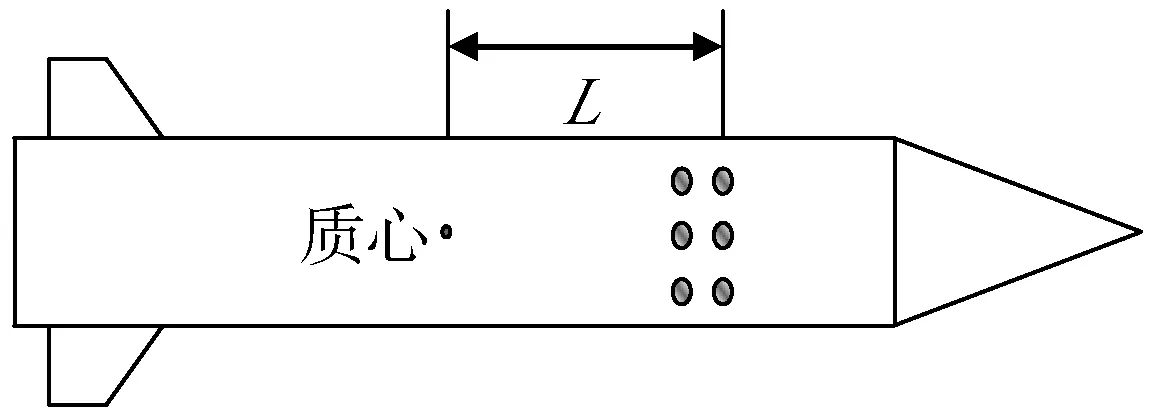
图7 脉冲发动机的布局Fig.7 Schematic of layout

仿真中考虑的仪器误差包括：GPS标准误差为水平定位为8 m，定高 12 m；速度标准误差为水平方向0.5 m/s，垂直方向0.6 m/s；地磁滚转姿态测量误差为2°；仿真中加入了1.2 m/s的横向风。

分别在无控条件下和有控条件下各进行200次仿真打靶试验。落点偏差的标准差和圆概率偏差(circular error probable,CEP)值见表1，图8为无控条件下弹丸的落点散布情况，图9为弹丸在有控条件下的落点散布情况。经过脉冲修正后，弹丸的落点精度CEP从176.3 m提高到36.7 m。

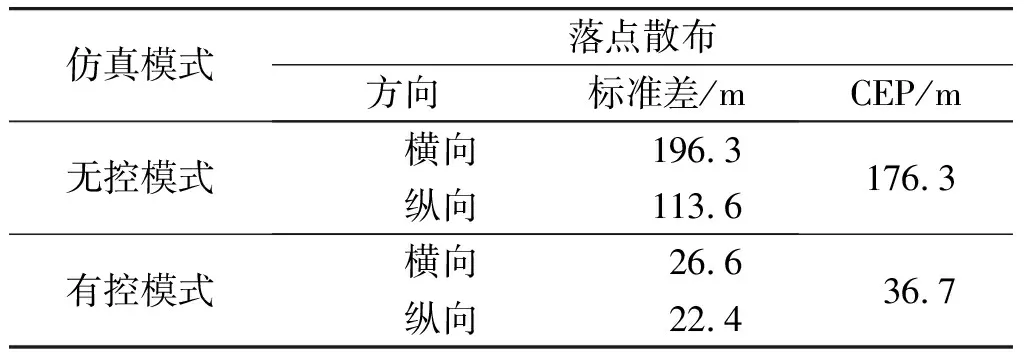
表1 仿真结果数值Table 1 Simulation results values

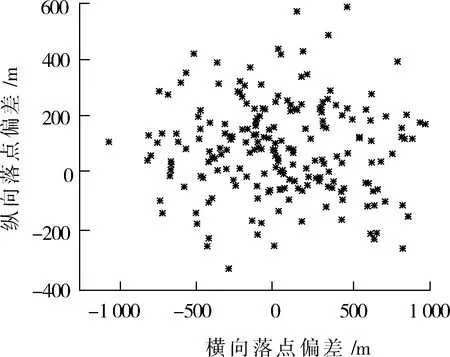
图8 无弹道修正的落点散布Fig.8 Impact point dispersion of uncontrolled ballistic

图9 弹道修正后的落点散布Fig.9 Impact point dispersion of trajectory correction

6 结束语

本文提出了一种基于摄动原理的落点预测算法。在发射前根据标准弹道获取样本点，以回归方法建立落点预测模型，将标准弹道和比例系数k装订到弹载计算机内。在弹丸飞行过程中弹载计算机根据位置和速度信息实时预测落点，并进行弹道修正。仿真结果表明，采用该算法能够大幅提高弹道修正弹的落点精度。

参考文献：

[1] 赵悍东,郭锡福,王芳.侧推矢量在提高火箭弹射击精度的技术研究[J].弹箭与制导学报,2005，25(2):72-74.

ZHAO Han-dong,GUO Xi-fu,WANG Fang. Research on Thruster Firing Rockets Vector in Improving the Accuracy of Technical[J].Journal of Projectiles Rockets Missiles and Guidance,2005，25(2):72-74.

[2] 徐劲祥.末段修正迫弹脉冲修正方案研究[J].弹箭与制导学报,2005,25(1):50-52.

XU Jin-xiang. Research on Terminal Correction Impulse Correction Scheme[J]. Journal of Projectiles Rockets Missiles and Guidance, 2005,25(1):50-52.

[4] JITPRAPHAI T,COSTELLO M.Dispersion Reduction of a Direct Fire Rocket Using Lateral Pulse Jets[J]. Jour-

nal of Spacecraft and Rockets,2001,38(6):929-936.

[5] THANAT J, BRADLEY B, MARK C. A Comparision of Different Guidance Schemes for a Direct Fire Rocket with a Pulse Jet Control Mechanism[R].ARL-CR-493, 2002.

[6] 曹营军，杨树兴，李杏军.基于脉冲控制的末段弹道修正弹点火相位优化研究[J]. 弹箭与制导学报, 2008,29(8):897-901.

CAO Ying-jun, YANG Shu-xing,LI Xing-jun.Research on Firing Phase Angle Optimization of Terminal Trajectory Correction Projectile Based on Pulse Jet Control[J].Acta Armamentarii, 2008,29(8):897-901.

[7] Anthony J Calise,Hesham A EI-Shirbiny. An Analysis of Aerodynamic Control for Direct Fire Spinning Projectiles[R].AIAA 2001-4127,US:AIAA, 2001:5-7.

[8] 张成，曹营军，杨树兴.一种低速滚转弹药脉冲发动机弹道修正方法[J].弹道学报,2008,20(2):45-48.

ZHANG Cheng,CAO Ying-jun,YANG Shu-xing. A Method of Ammunition Pulse Engine Speed Roll Trajectory Correction[J]. Journal of Ballistics,2008,20(2):45-48.

[9] 姚文进，王晓鸣，高旭东，等.弹道修正弹脉冲修正机构简易控制方法[J].弹道学报,2007,19(3):19-22.

YAO Wen-jin,WANG Xiao-ming,GAO Xu-dong,et al.Method for Impulse Correction based on Trajectory Torrection Trojectile Simple Control[J]. Journal of Ballistics,2007,19(3):19-22.

[10] 王中原,涂四华，艾东民，等.弹道修正中弹道诸元探测时间间隔的确定[J].弹道学报,2002,14(1):84-87.

WANG Zhong-yuan，TU Si-hua,AI Dong-min,et al. Ballistic Trajectory Correction in Moroto Probe to Determine the Time Interval[J]. Journal of Ballistics, 2002,14(1):84-87.

[11] 钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M]. 北京: 北京理工大学出版社, 2000.

QIAN Xing-fang, LIN Rui-xiong,ZHAO Ya-nan. Aerothermodynamics of Missile Flight[M].Beijing:Beijing Institute of Technology Press，2008:36-48.

[12] GAO Feng,ZHANG He. Study of 2-D Trajectory Correction Based on Geomagnetic Detection with Impulse Force for Projectiles[J].Journal of System Simulation, 2011,23(1):123-128.