机械陀螺稳定式激光导引头建模与仿真*
任京芹
(西安工业大学北方信息工程学院,陕西 西安 710032)
0 引言
激光导引头用来完成对目标的搜索、识别和跟踪,并给出制导律所需要的控制信号,在制导过程中,确保制导系统不断地跟踪目标,形成控制指令,送入自动驾驶仪,操纵导弹飞向目标,在战术武器的应用中取得了惊人的成绩[1-2]。由于导引头属于机、光、电、磁的综合类产品,其系统数学模型的建立对于导引头设计过程中性能参数匹配具有一定的指导意义。
1 激光导引头组成原理
导引头作为重要的制导部件,采用三自由度陀螺稳定位标器作为跟踪机构,接收目标漫反射的激光能量,经光学系统会聚于探测器焦平面,并由探测器转换为描述目标视线和位标器光轴之间角误差的电信号,输出给电子舱进行处理;处理后的误差跟踪指令信号加到陀螺系统的进动线圈,产生进动力矩驱动光学系统对目标进行跟踪,使光轴指向目标,实现对目标视线角速度的测量,完成制导控制任务[3],其工作原理如图1所示。

图1 激光导引头控制原理Fig.1 Control principle of the laser seeker
陀螺稳定式位标器主要由透射式光学系统、光电探测器、万向支架、转子及平衡环、章动阻尼器、解锁和加速机构组成[4-5],待导引头捕获目标后,在解锁和加速机构的作用下,位标器陀螺迅速加速至稳定转速,在进动线圈的作用下实现对目标的自动跟踪,其基本组成结构如图2所示。

图2 位标器的组成结构图Fig.2 Component of the laser seeker
2 动力学建模与仿真
陀螺解锁前陀螺坐标系与弹体坐标系重合,陀螺解锁后随着弹体的纵向、横向、滚转以及陀螺进动等运动,为保持陀螺在指定方向上的定向性,陀螺内外框也要随着摆动,实现位标器的稳定跟踪。因此,设初始时刻弹体与导引头光轴均无偏转,弹体、外环与内环各轴对应平行,且均平行于地面坐标系,当弹体姿态、光轴姿态发生变化时,导引头测量系与弹体系之间的变换关系可由它们之间的坐标变换矩阵得到。
2.1 激光探测器误差角建模
根据动力学建模的需要,这里需要定义4个坐标系[6],分别为:地面坐标系Oxyz,原点O选取在导弹发射点,Ox在弹道面内指向目标为正,Oy轴在弹道面内垂直于Ox轴向上为正,Oz轴垂直于Oxy面满足右手坐标系;弹体坐标系O1x1y1z1,原点O1选在导弹的瞬时质心上,O1x1轴与弹体纵轴重合,指向头部为正,O1y1位于弹体纵向对称面内与O1x1垂直,指向上为正,O1z1轴垂直于O1x1y1面满足右手坐标系;测量坐标系O2x2y2z2,原点O2选在探测器;导引头视线角坐标系O3x3y3z3,坐标系之间的角度转换关系如图3所示。

图3 坐标系转换关系Fig.3 Relationship of coordinate conversion
按照坐标定义可以知道对位标器陀螺起主要进动控制的变量是探测器测量坐标系与视线角坐标系之间的角度误差角Ey和Ez,按照地面坐标系→测量坐标系→视线角坐标系=地面坐标系→视线角坐标系,可以求得对应的误差角方程为
sinEz= -cosqzcosqysinθlcosφl+
sinqzcosθl-cosqzsinqysinθlsinφl,
sinEy=cosqzsin(qy-φl)/cosEz,
(1)
式中:qy和qz为视线坐标系的2个方向上的视线角,由弹体和目标相对位置关系决定,可表示为
(2)
式中:(xt,yt,zt),(xm,ym,zm)分别为目标和导弹在地面坐标系下的位置坐标。
φl和θl是地面坐标系到测量坐标系的测量方位角和俯仰角,其值可根据图3用地面坐标系→弹体坐标系→测量坐标系求出。为求出φyφz根据环架结构和复合运动原理,导引头光轴的指向运动由内外环和弹体的运动合成得到[7],即

(3)
式中:ωx2,ωy2和ωz2为位标器陀螺在进动力矩作用下的进动角速度;φz和φy为陀螺框架角的内外框的角度;ωx1,ωy1和ωz1分别为弹体姿态的3个角速度。经变换可以得到陀螺内外框运动角速率方程为
(4)
求出φyφz结合弹体姿态角可求出φl和θl,由式(1)可求出误差角Ey和Ez。
2.2 激光导引头位标器原理建模
激光导引头用四象限光电元件作探测器,根据光斑在四象限上的位置来确定目标的方位角信息,即导弹的横向偏差和纵向偏差[8-10],四象限探测器元件采用和差电路定向方法,其原理如图4所示。
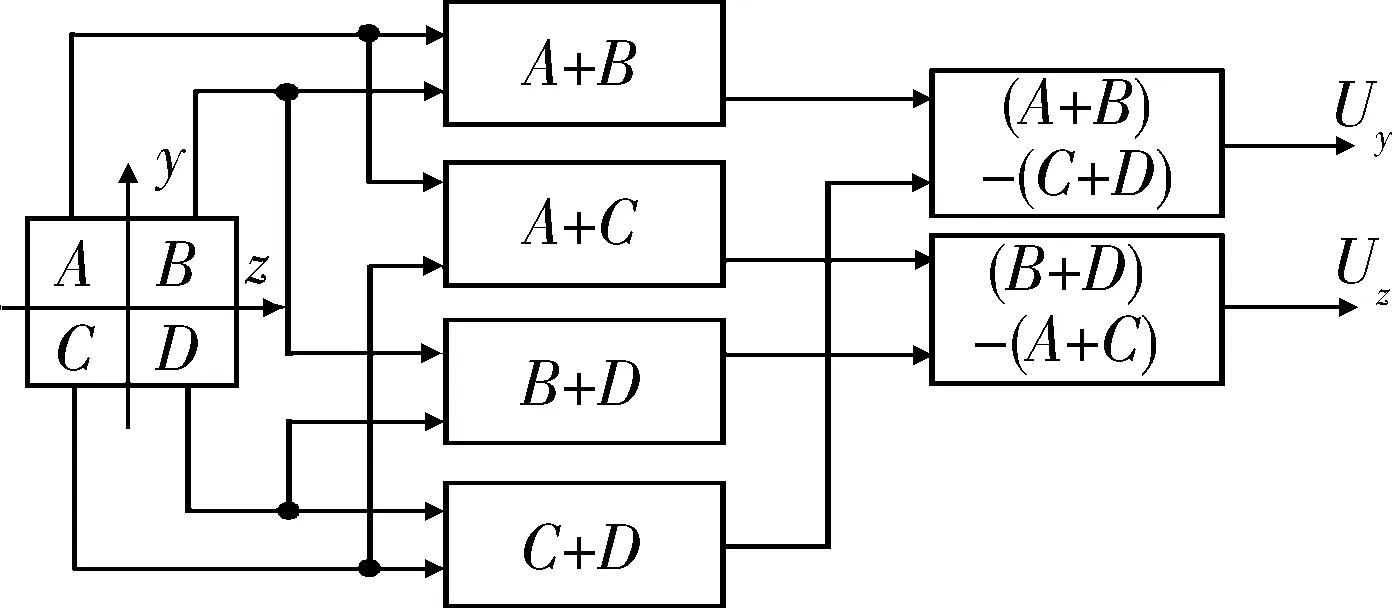
图4 四象限元件的定向原理Fig.4 Four quadrant cell orientation principle
以四象限的中心为坐标原点,十字交叉线为直角坐标系的y轴和z轴,光斑中心的坐标为(y,z),光斑半径为r,现在假定光斑是均匀分布的,系统的输入信号为激光光斑中心的位置坐标,输出信号为驱动位标器陀螺转子转动的电压信号(Uok1,Uok2)。输出位标器陀螺进动力矩控制电压与光斑大小成正比,当目标偏离光斑中心时,用和差法通过光斑大小可直接确定输出电压的大小。若探测器完全对准目标中心,即(y=0,z=0)各象限输出电压相等,则(Uok1=0,Uok2=0),否则位标器陀螺进动力矩控制电压可以表示为
(5)
组成导引头系统的主要环节有激光探测器、主放大器、峰值保持器、和差运算、归一化电路、功放和陀螺伺服机构。通过对各组成部分的机理进行分析,从探测器到功放之间的各个部分都可以简化为比例环节,可以得到总的传递系数k0=2.73。
当目标中心不在跟踪系统的光轴上,则光斑中心偏离零点。假设弹目距离为R,探测器的焦距为f。目标到光轴与地面交点的距离为(Oy,Oz),光斑在探测器上的偏移坐标为(y,z),根据相似三角形原理可以知道目标角度偏差量可以表示为
(6)
y=ftanEy,z=ftanEz.
(7)
利用式(1)解出Ey和Ez,由式(7)解出y和z,将y和z代入式(5)可以计算出陀螺进动控制的输出电压Uok1和Uok2。
2.3 位标器陀螺动力学模型的建立
建立位标器陀螺的动力学模型,根据陀螺的机构和陀螺力学原理考虑到陀螺是对称回转体,不考虑x方向的阻尼力矩及干扰力矩引起的角速度变化的影响,陀螺在测量坐标系内所受到的动量矩方程为[11-12]
(8)
式中:φy2和φz2为位标器陀螺在两坐标系下的偏航与俯仰方向的角运动;Hg为陀螺绕x轴的动量矩;My2和Mz2为位标器陀螺的偏航和俯仰方向的进动力矩。
根据导引头指令信号特征(周期为50 ms,工作区为40 ms,非工作区为10 ms),可以把每个周期形成的指令按照阶跃函数来计算。位标器陀螺的偏航和俯仰方向进动力矩大小的计算,在导引头中,作用在陀螺上的力矩是由永久磁铁的磁场和进动线包上的磁矩作用产生的力矩来确定的。根据陀螺转子磁铁和线包结构的特征,按照陀螺转子永久磁铁的磁场和线包磁矩相互作用产生进动力矩的工作原理,经过推导可以得到陀螺的进动力矩表达式为
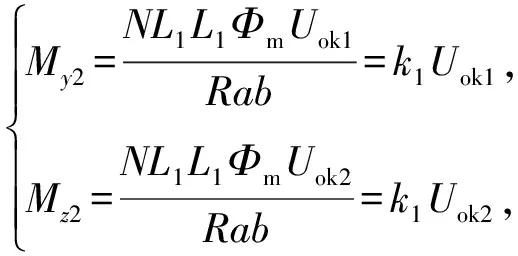
(9)
式中:N为线圈匝数;L1L1为线圈的面积(单位为cm2);Φm为通过线圈的磁通量(单位为Wb);ab为线圈的截面积(单位为cm2);Uok1和Uok2为作用在线圈上的电压(单位为V),也就是导引头输出的进动控制电压。
通过式(9)可以看出线圈匝数、线圈面积、磁通量等均可近似为常值,即位标器的陀螺进动力矩与进动控制电压呈比例系数为k1的线性关系。通过测试计算可知某激光导引头k1≈6.5。
将式(8)经过拉氏和反拉氏变化可以得到陀螺俯仰和偏航方向的角速率表达式为
(10)
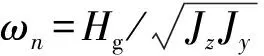

(11)
式(11)为陀螺在驱动力矩作用下的进动力学简化模型,利用该模型实现位标器跟踪视线角的进动形成闭环控制回路。
3 仿真验证分析
通过上述分析完成了导引头控制系统闭环回路建模。即:根据弹目相对位置、导弹姿态信息以及位标器陀螺运动情况确定探测器测量系与视线角坐标系误差角→位标器根据误差角形成陀螺进动控制电压→位标器陀螺进动→修正误差角。根据建立的模型,对某激光导引头进行建模仿真分析。

(1) 在激光探测器没有激光信号作用时,位标器陀螺只起到稳定平台的作用,弹体振动与陀螺内、外框架角的振动角度变化情况如图5,6所示。

图5 陀螺内框与弹体俯仰角变化Fig.5 Gyroscope inner frame and shell body pitch angle changes
从图5~6可以看出陀螺框架角度变化与弹体角度变化振幅(0.795 8°)相等,方向相反,可以较好地保持平台稳定作用。
(2) 在探测器捕获到目标以后,按照探测器误差角的大小控制进动力矩驱动陀螺跟踪目标,陀螺在进动力矩作用下和弹体摆动角度变化曲线如图7,8所示,激光光斑在探测器上的偏移坐标为(y,z)的变化曲线如图9,10所示,进动力矩驱动电压(Uok1,Uok2)的变化曲线如图11,12所示。

图6 陀螺外框与弹体偏航角变化Fig.6 Gyroscope frame with shell body yaw angle changes

图7 在进动力矩作用下陀螺内框与弹体俯仰方向的运动Fig.7 Under the action of the precession torque gyroscope inside frame and pitch direction moment of the shell
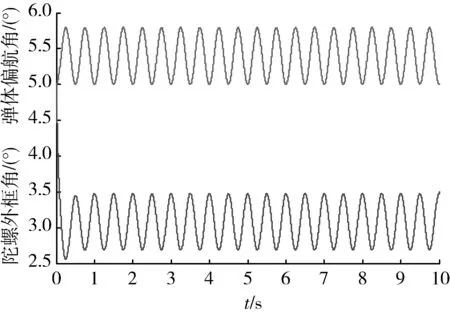
图8 在进动力矩作用下陀螺外框与弹体偏航方向的运动Fig.8 Under the action of the precession torque gyroscope outside frame and yaw direction moment of the shell

图9 探测器坐标面内y偏差变化Fig.9 y deviation change in the detector coordinate plane

图10 探测器坐标面内z偏差变化Fig.10 z deviation change in the detector coordinate plane

图11 电压Uok1变化Fig.11 Voltage changes of Uok1

图12 电压Uok2变化Fig.12 Voltage changes of Uok2
通过仿真结果可以看出按照给定的导引头参数及弹体的运动状态,由图8~11可以看出位标器在0.5 s内即可快速地跟踪到目标,并且由图6,7可以看出位标器一直处于稳定状态,与导引头指标参数基本一致,验证了仿真结果的可行性。
4 结束语
本文按照激光导引头的工作原理,对其进行了数学建模,通过仿真对所建立的模型进行了分析,验证了数学模型的可行性。该模型可与弹道计算模型同时使用,实现制导弹药有控段导引头工作的全弹道数学仿真,可以有效分析导引头在不同工况和物理量参数条件下的性能指标,为激光导引头的设计提供理论支撑。
参考文献:
[1] 郜开开,王佳民,王卿. 精确制导武器的导引头综述[J].科技创新导报, 2011(34):11.
GAO Kai-kai , WANG Jia-min,WANG Qing.The Overview of the Precition Guided Weapon Seeker[J].Science and Technology Innovation Herald,2011(34):11.
[2] 孟秀云. 导弹制导与控制系统原理[M].北京理工大学出版社,2002:168-169.
MENG Xiu-yun. The Principle of the Guide and Control for Missile[M].Beijing:Beijing Institute of Technology Press,2002: 168-169.
[3] 李慧,吴军辉,朱震,等.速率陀螺式激光导引头稳定跟踪原理分析与仿真[J].激光与红外,2011,40(7)1339-1340.
LI Hui,WU Jun-hui,ZHU Zhen,et al. Analysis and Simulation of Stabilization and Tracking Principle or Rate Gyroscope Laser Seeker[J]. Infrared and Laser Engineering,2011,40(7):1339-1340.
[4] QI Zai-kang,XIA Qun-li.Guided Weapon Control Systems[M].Beijing:Beijing Institute of Technology,2004:271-287.
[5] 邓潘. 浅析激光半主动寻的制导系统[J]. 制导与引信, 2008,29(4):15-20.
DENG Pan. Analysis of the System of Laser Semi-Active Homing Guidance[J]. Gudidance & Fuze,2008,29(4):15-20.
[6] 吕学富.飞行器飞行力学[M].西安:西北工业大学出版社,1995: 48-54.
LÜ Xue-fu. Flight Dynamic of the Flight Vehicle[M].Xi’an: Northwestern Polytechnical University Press,1995:48-54.
[7] 李慧,吴军辉,胡欣,等.动力陀螺式激光导引头的动力学建模与仿真[J]. 激光与红外, 2011,41(7). 759-761.
LI Hui,WU Jun-hui,HU Xin,et al. Dynamic Modeling and Simulation of Dynamic-Gyro Laser Homing Head[J]. Laser and Inreared,2011,41(7):759-761.
[8] 魏文俭,秦石乔,战德军,等. 激光仿真导引头陀螺稳定控制的研究[J]. 激光与红外, 2008,37(增刊1): 298-302.
WEI Wen-jian,QIN Shi-qiao,ZHAN De-jun,et al. Research on the Gyro’s Steady Control of Some Laser Simulation Seeker[J]. Infrared and Laser Engineering,2008,37(S1): 298-302.
[9] 邢晖,雷萍,吕鸿鹏,等. 半主动式激光导引头跟踪角误差的分析与测试[J].光电工程, 2012,39(4): 79-82.
XING Hui,LEI Ping,LÜ Hong-peng,et al. Analysis and Test of Tracking Angle Error for Semi-Active Laser Seeker[J]. Opto-Electronic Engineering,2012,39(4):79-82.
[10] 何衡湘,陈亦庆,赵刚,等. 激光导引系统主要技术参数分析[J]. 红外与激光工程, 2009,38(3):428-431.
HE Heng-xiang,CHEN Yi-qing, ZHAO Gang,et al. Analysis of the Main Parameters of the Laser Guided System [J]. Infrared and Laser Engineering,2009,38(3):428-431.
[11] 刘敏. 某型激光导引头光电系统建模与测试方法研究[J]. 光学技术,2008,34(2)189-192.
LIU Min. Research of the Hardware-in-the-Loop Simulation System for Laser Seeker[J]. Optical Technique,2008,34(2):189-192.
[12] 朱华征,范大鹏,马东玺,等. 导引头伺服系统隔离度与测试[J]. 光学精密工程,2009,17(8):1994-1998.
ZHU Hua-zheng, FAN Da-peng, MA Dong-xi,et al. Disturbance Isolation Index of Seeker Servo System and its Test[J]. Optics and Precision Engineerin,2009,17(8):1994-1998.

