主动防护系统探测雷达的目标跟踪*
李慧敏,李斌,马可,刘代
(西安电子工程研究所,陕西 西安 710100)
0 引言
“硬杀伤”主动防护系统[1-5](后文中将简称为主动防护系统)通过发射反击弹药对来袭目标进行拦截,在拦截区域爆炸形成破片流来摧毁或者杀伤目标,使其丧失攻击能力或效能降低。要准确杀伤目标,火控计算机必须提供准确的目标位置、航向、速度等信息。反击弹药从准备发射到飞至拦截点爆炸,耗费时间为t(10-2秒数量级),这要求火控计算机预测t秒后目标所在位置,即对目标位置进行外推,确定拦截点位置,进而选择合适的反击弹药进行拦截。
对于高速目标,在雷达有效探测范围内的飞行时间短、外推距离长,利用传统卡尔曼滤波算法[6-8]进行目标跟踪时,算法不能充分收敛,导致外推精度较差。本文在分析主动防护系统工作过程的基础上,针对其中目标跟踪的特殊性,提出将跟踪问题划分为目标到达时间估计和反击弹药选取2个部分,分别求解,提供了一种可行的思路。
1 主动防护系统工作过程
首先介绍主动防护系统的工作过程,为后面分析目标跟踪的特殊性打下基础。
如图1所示,主动防护系统的工作过程[9]主要分为以下几个阶段:目标搜索、开始跟踪、滤波并外推、发射反击弹药、完成拦截。
主动防护系统中目标搜索和跟踪由极近程探测雷达来完成,该雷达一般采用连续波体制,具有测距精度高、近距无模糊等优点,但由于众所周知的收发隔离问题,严重制约了连续波雷达的探测距离。考虑最严峻的情况,极近程探测雷达的探测距离在百米之内,减去到由搜索转跟踪时间内目标的移动距离,因此对目标的有效跟踪数据最远从几十米处开始。另外,在实战中,敌方武装分子一般也选择在近距对装甲车辆实施攻击,因此即使雷达探测距离可以更远,默认有效数据开始于几十米处也是合理的。

图1 主动防护系统的工作过程Fig.1 Working process of active protection system
由于目标距离近,速度快,为了保证可靠的跟踪,极近程探测雷达必须保持较高的数据率,为数据处理单元提供充足的观测数据。直观来说,数据率越高,相同时间内的观测数据也越多,因此更利于滤波算法的收敛。但过高的数据率无疑增大了雷达信号处理单元和数据处理单元的运算量,对处理器的运算速度提出了很高的要求,因此可能反而不符合主动防护系统快速反应的要求。此外,数据率过高,相邻数据的相关性将大大加强[9],对提高滤波精度没有多大帮助,徒增了数据处理的压力[9]。根据现有文献,数据率一般在0.5~2 ms左右。
近程防护中的来袭目标具有2个特点:距离近,速度快。进行如下假定:
(1) 装甲车辆在目标攻击时间内是静止的,这是因为目标速度持续时间短(10-2s数量级),这段时间内车辆的位置变化可以忽略不计。
(2) 目标作直线运动。由于目标飞行时间短,不管对于动力飞行目标,还是惯性目标,竖直方向上重力加速度的影响都很小。
(3) 目标在直线航路上仅作加速或减速运动。
从图1可以看出,目标从外推位置飞到拦截面的耗时与反击弹药点火并在拦截面处炸开所需的时间是相等的。当拦截位置与车辆的距离固定时(10~30 m不等),反击弹药的飞行时间t是个确定值。因此目标跟踪的主要任务是:根据滤波值实时估计目标飞到拦截面所需的时间t’,当时,确定目标与拦截面的交汇位置,指导反击弹药延时t’∈(t,t+δ)后发射反击(其中δ为小于雷达数据更新率的一个小值)。
目标速度确定时,反击弹药反应时间t越长,外推点离拦截点的距离就越远,滤波算法的外误差也越大。因此,反击弹药反应时间越短越好,但受限于物理机制,反应时间存在下限值。另一方面,目标速度越快,外推点离拦截点的距离就越长,此消彼长,可用来滤波的距离段对应的数据却越少,因此,矛盾集中于高速目标的跟踪和外推。
2 目标跟踪
2.1 卡尔曼滤波的不足
卡尔曼滤波方法[6,10]在工程实际中得到了广泛应用。在一般情况下,卡尔曼滤波及其延伸算法可以很好地满足应用要求。文献[9]和文献[11]讨论了卡尔曼滤波器在近程防护中的应用,得到了有益的结果。与本文设定的参数相比,其目标跟踪时间、距离相对较长,算法得到了比较充分的收敛,但对于本文设定的极近程高速目标跟踪与外推这种极端情况,其性能难以满足应用要求。此外,卡尔曼滤波是一种性能与模型相关的跟踪算法,若模型与目标实际情况不匹配,将导致较大的误差,而实际战场环境中,不同目标的动态很大,如目标速度从几十米每秒到近千米每秒,加速度范围从1g到十几g(g为重力加速度),单一模型的卡尔曼滤波器很难覆盖这么多种目标,并均达到良好的滤波效果。
即使目标模型准确,但对于高速目标(例如>700 m/s),由于可用于滤波的有效观测点数少,算法难以充分收敛,由观测矩阵输出的速度、加速度的滤波值和真实值偏差较大,只有位置滤波值相对较为准确,由此估计出的拦截点位置偏差较大,难以满足拦截要求。
2.2 反击拦截简化
最理想的拦截是反击弹药瞄准预推的拦截点进行发射,给予来袭目标“迎头痛击”,这种拦截方式的拦截效率最高[12]。但反击弹药的瞄准是一个机械控制的过程,反应速度相对较慢,难以适应快速反击的要求。根据国际上已装备的主动防护系统,反击弹药一般都采用了固定安装,每枚反击弹药对特定的方位角区域构成防护,通过在车辆周边各角度上均匀安装多枚反击弹药,同时使各枚弹的防护区域稍稍交叠(见图2),就可以构成360°的严密防护。反击时,只要预先判断目标会出现在那个防护区,选择对应的反击弹药进行拦截即可。

图2 坦克防护区域设计Fig.2 Design of protection coverage for tank
根据反击弹药拦截目标的特殊性,可将目标跟踪外推分解为2个部分:一是准确估算目标飞到拦截面所需时间(简称到达时间);二是判断目标会飞到哪枚反击弹药的防护区域(即反击弹药的选取)。通俗来讲,就是确定什么时候打、谁来打的问题。将跟踪滤波问题进行分解后,2个部分可以单独求解,这利于分别选取更灵活、高效的算法。
根据2.1节的讨论可知,卡尔曼滤波方法的劣势就在于对运动模型具有依赖性,当目标实际模型与假设的模型差异较大时,误差将逐步累积,导致滤波发散。所以在设计滤波方法时,要避免累积误差带来的影响,思路之一就是利用滑窗滤波,只利用最近的几个观测值对目标进行估计,而忽略之前的观测数据,使模型失配的影响降低。
2.3 新的处理方法
考虑用如下方法进行目标跟踪与外推。
2.3.1 到达时间的估算
不考虑加速度时,利用目标的距离信息和速度信息即可估计目标到达拦截面的时间,根据2.1节的讨论,可知使用卡尔曼滤波时,对于高速目标,速度的滤波值误差较大,不能满足要求。
近程防护中目标的特殊性在于,目标飞行方向必定朝向车辆。探测雷达安装在车辆某一固定位置上,因此雷达观测到的目标径向速度接近于真实速度,两者的关系可通过如图3来表示。

图3 真实速度与径向速度关系图Fig.3 Relation of actual velocity and radial velocity
图3中ΔR为目标飞行路线偏离雷达的距离,只考虑水平方向的偏离时,即为航路截径。真实速度和径向速度之间的夹角为θ,且随着距离的减小而逐渐变大。当ΔR取不同值时,真实速度和径向速度的关系如图4所示。
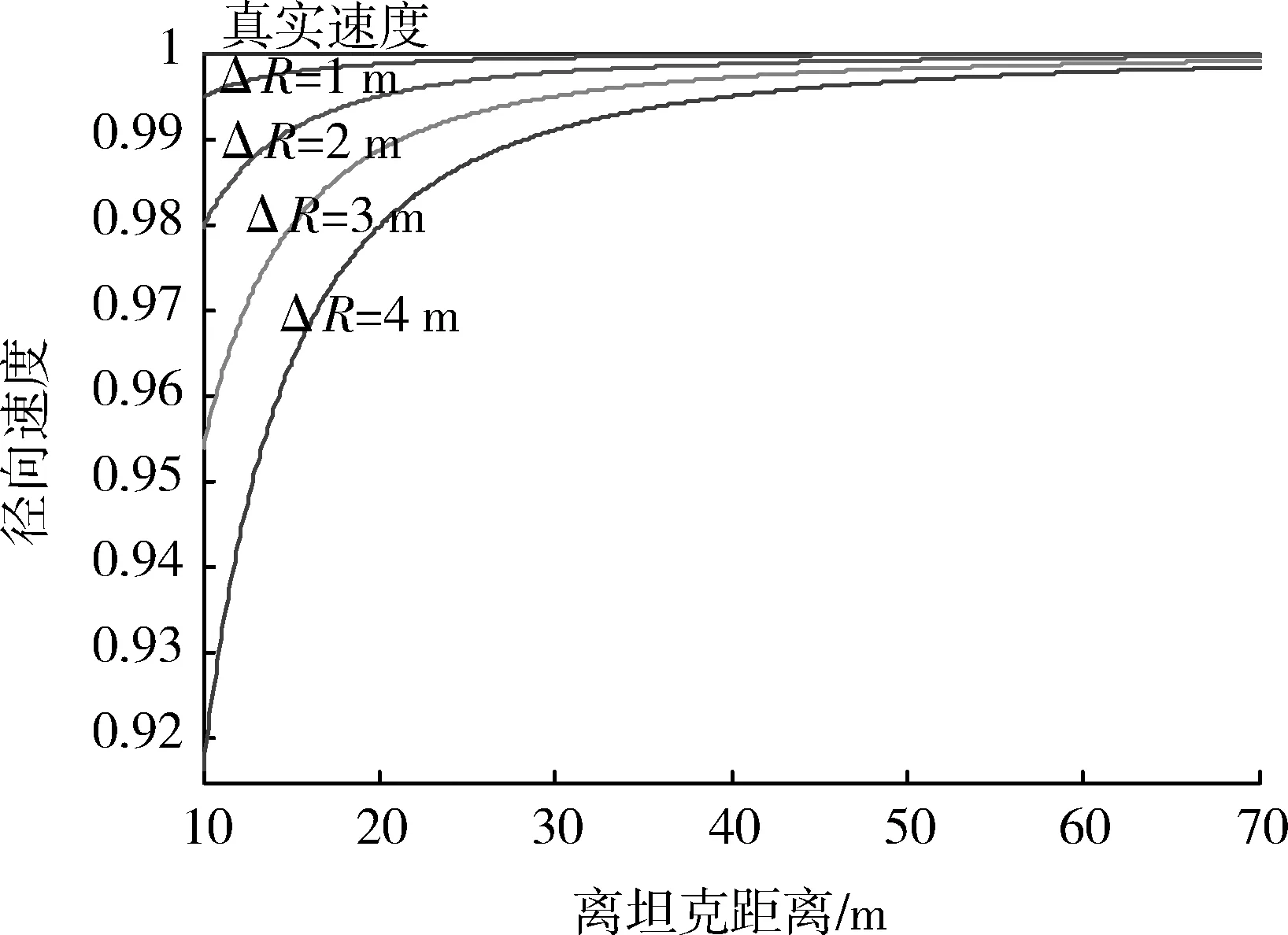
图4 径向速度与真实速度随目标距离的变化Fig.4 Relation of actual velocity and radial velocity versus target distance
由于径向速度是真实速度的径向分量,所以其大小始终小于真实速度。当ΔR一定时,随着目标的迫近,真实速度和径向速度之间的差值逐渐增大。以ΔR=4 m为例,从70~30 m之间,二者的偏差逐渐增大到约1%,可见偏差不是很大。另外,ΔR越小,二者之间偏差也越小。所以可以考虑用径向速度代替真实速度。但这不意味着可以用径向速度矢量代替真实速度矢量,可以简单证明,在低仰角情况下,垂直方向的速度和真实速度在该方向的分量偏差较大,由此进行滤波时,将在垂直方向上造成较大的误差,因此只有将径向速度以标量形式代替真实速度才是合适的。
目标离拦截面的距离(R2)可以用目标的斜距(R1+R)与雷达到拦截面的距离(R)之差来代替,示意图如5所示。
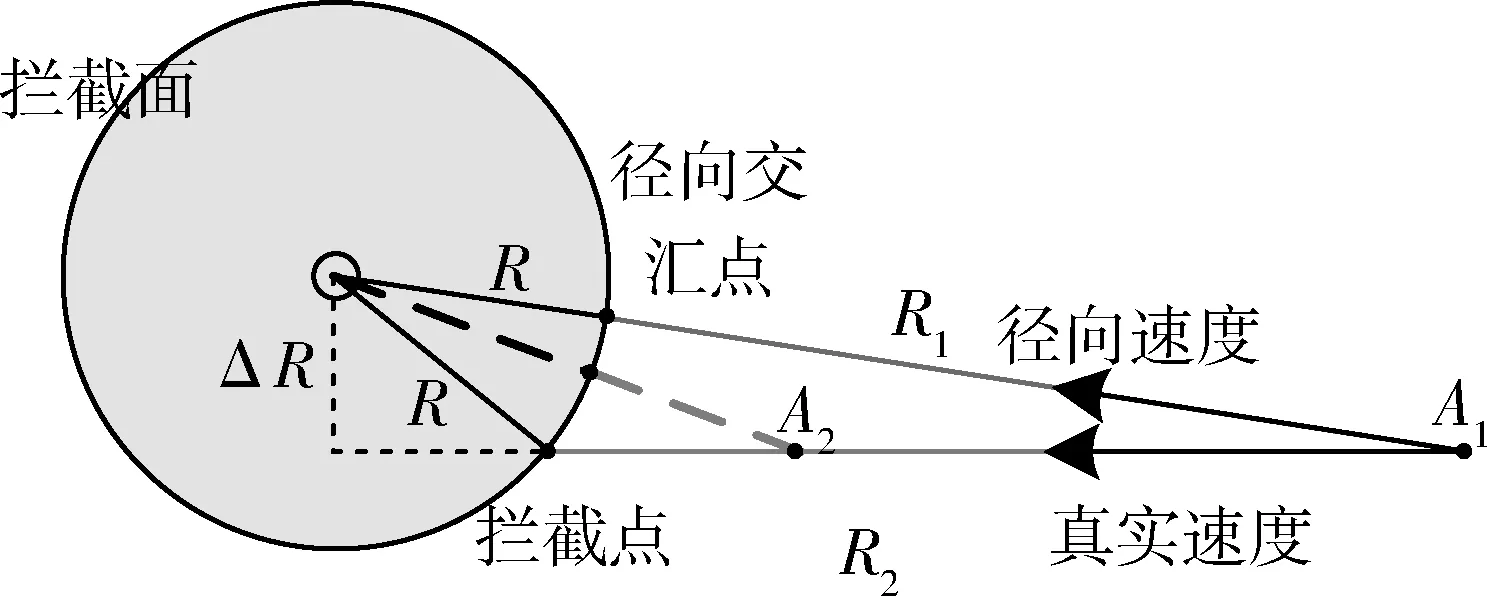
图5 距离估计偏差示意图Fig.5 Range estimation error
由简单三角关系可知R2>R1,且始终成立。随着目标的靠近,二者的差值变小,例如从位置A1到达位置A2时。所以估计的距离始终偏小,而根据上文可知,估计的速度值也偏小,所以二者相除得到的到达时间反而可能与真实值接近。时间估计误差乘以目标真实速度即为引起的距离估计偏差,目标作匀速运动时,距离估计偏差如图6所示。

图6 距离估计偏差随目标距离的变化Fig.6 Range estimation error versus target distance
图6反映了2个信息:①ΔR越大,估计引起的距离偏差(即距离延后量)越大;②目标离坦克越近,估计引起的距离偏差越小。
图6中纵轴为距离延后量,该值总是大于0,说明对于匀速目标,估计的到达时间始终偏小,反击弹药总是过早发射!实际应用中可以对此进行补偿(例如,对各种情况统一作0.3 m延后补偿,使图6中偏差曲线整体下移0.3 m,补偿后误差的绝对值最大为0.3 m左右)。对于匀加速目标,补偿量要适当减小,反之,对于匀减速目标,补偿量应略微增大。
上面说明了利用目标斜距和径向速度可以比较准确地估计目标的到达时间。实际中,由于存在测量噪声,所以通过最简单的滑窗均值滤波方法求目标的径向速度和距离,步骤如下:
(1) 对tn-N+1,…,tn时刻(窗宽为N)的径向速度vn-N+1,…,vn求平均,得到径向速度滤波值

(3) 根据R0和时标tn计算出目标的当前位置
由于滤波仅利用了离当前观测时刻最近的3~10个观测值,所以避免了模型不匹配带来的累积误差。由于滤波所需点数少,所以对于高速目标,也可准确地估算到达时间,这点意义重大。此外,滤波时只包含两维数据,计算量小,且观测误差相互独立,处理简单。
2.3.2 反击弹药选取
根据假设,来袭目标作直线运动,所以只要确定目标的航向,根据航向与防御面的交汇情况,选择相应反击弹药进行拦截即可。使用最小二乘方法对目标的位置观测数据进行直线拟合,该算法可递归实现[4]。对于低速目标,外推点之前获取的观测数据较多,进行直线拟合后,所得滤波航路和目标真实航路之间的偏差较小,示意图如图7所示。

图7 低速目标x-y平面上的直线拟合Fig.7 Straight line fitting of low speed target on x-y plane
图7是对低速目标观测数据在x-y面(即水平面)上的投影进行直线拟合的结果。可见滤波后的航路和真实航路几乎完全重合,直线拟合精度高,因此可以准确地判断目标将会和哪枚反击弹药的防护区域相交,因此可以准确选弹。
选弹的难点仍在于高速目标,高速目标在外推点之前的观测数据较少,直线拟合误差较大,示意图如图8所示。

图8 高速目标x-y平面上的直线拟合Fig.8 Straight line fitting of high speed target on x-y plane
图8同样为目标x-y面上观测数据的直线拟合结果,由于观测点数少,使得滤波航路和真实航路之间的偏差较大(拟合误差的具体大小由雷达的测量精度决定)。设拟合误差引起的选弹方位角误差为ψ,则目标可能出现的方位角范围为2ψ(称作威胁范围),若2ψ大于一枚反击弹药覆盖的方位角,则目标的威胁范围最多会覆盖到3枚反击弹药的防护区域,也就是说需要3弹齐发,同时反击。
对于高速目标,当直线拟合误差过大时,选弹时拟采取以下策略:考虑以目标在外推点的观测方位为准,指导反击(称为次优选弹法)。可以计算出目标到达防御面之前(取10 m)方位角的变化情况,如图9所示。

图9 目标移动引起的方位角变化量Fig.9 Azimuth angle change versus target distance variation
从图1中可以看出,ΔR=4 m时,若外推点在60 m处,则目标从外推点开始到防御面处的方位变化最大值约为20°;ΔR=3米时,变化值约为15°;ΔR=2 m时,变化约为10°。
实际情况中,若假定90%的目标攻击路线偏离中心的距离ΔR<2 m,则目标方位角变化最大不超过10°,以此作为次优选弹法的方位角误差。
对比次优选弹法与直线拟合法的选弹方位误差,择优选定。具体选择哪种方法,需要根据雷达的测量精度具体确定。
根据仿真结果,在雷达的测量精度不是很高的情况下(测角误差为2°,测距误差1 m),对于高速目标,次优选弹法效果更好。次优选弹法的劣势是不能确定目标的航向,从而无法判断目标是否会真正打到坦克,可能诱发虚假反击。对于低速目标,直线拟合法可以准确选弹。
3 结束语
本文简要介绍了主动防护系统的特点以及其作战过程,分析了这种条件下目标跟踪问题的特殊性,然后针对性地将目标跟踪外推问题分解为到达时间估计、反击弹药选取2部分,使跟踪滤波问题得到了简化,便于更灵活地进行滤波算法选取。
通过对目标斜距和径向速度进行滤波,可以较准确地估算目标到达拦截面所需的时间,而且该方法对于高速、低速目标的效果均衡。另外,通过对目标进行固定运动补偿,可以使算法适用范围更广。
提出直线拟合选弹和次优选弹2种办法来进行反击弹药选择,这2种方法孰优孰劣,要因雷达的测量精度而具体确定。工程上,可以考虑根据速度对目标进行分类,建立2种算法的精度对比表,然后根据目标的观测速度,查表确定具体使用哪种方法进行选弹。
参考文献:
[1] 周子朴. 主动防护系统[J]. 国外坦克,2006(6): 38-39.
ZHOU Zi-pu. Active Protection System[J]. Foreign tank, 2006(6): 38-39.
[2] 王雄高. 提高坦克生存力的新途径——主动防护、隐形技术和非常规装甲[J]. 国外坦克, 2004(4): 22-25.
WANG Xiong-gao. New Way to Improve the Survival Probability of Tank——Active Protection, Stealth Technology and Unconventional Armor[J]. Foreign Tank, 2004(4): 22-25.
[3] 徐平. 主动防护系统总体技术的研究[J]. 车辆与动力技术,2008(1):58-60.
XU Ping. Research on Integrated Structure of Active Protection System[J]. Vehicle and Power Technology, 2008(1):58-60.
[4] 任晓刚. 国外坦克装甲车辆主动防护系统[J]. 火力与指挥控制,2010,35(S1):4-6.
REN Xiao-gang. Foreign Tank Armored Vehicle Active Protection System Introduction[J]. Fire Control and Command Control, 2010,35(S1):4-6.
[5] 文昱. 主动防护系统的研制动向[J]. 国外坦克,2004(2):5-7.
WEN Yu. Development Trend of Active Protection System[J]. Foreign Tank, 2004(2):5-7.
[6] 周宏仁,敬忠良,王培德. 机动目标跟踪[M]. 北京:国防工业出版社,1991.
ZHOU Hong-ren,JING Zhong-liang, WANG Pei-de. Track of Maneuvering Target[M]. Beijing:National Defense Industry Press, 1991.
[7] 蔡萌. 机动目标跟踪方法研究[D]. 哈尔滨:哈尔滨工业大学,2010.
CAI Meng. Research on Tracking Method of Maneuvering Target[D].Harbin: Harbin Institute of Technology, 2010.
[8] 王建华,张琳. 基于改进卡尔曼滤波方法的机动目标跟踪研究[J]. 现代防御技术,2006, 34(2):16-19.
WANG Jian-hua, ZHANG Lin. Maneuvering Multi Target Tracking Based on Correcting the Kalman Filter[J]. Modern Defence Technology, 2006, 34(2):16-19.
[9] 高学刚. 战车主动防护系统中的目标跟踪算法研究[D]. 南京:南京理工大学,2010.
GAO Xue-gang. Target Tracking Algorithm for Active Protection System of Armored Vehicle[D].Nanjing: Nanjing University of Science and Technology,2010.
[10] 何子述,夏威. 现代数字信号处理及其应用[M]. 北京:清华大学出版社,2009.
HE Zi-shu, XIA Wei. Theory and Application of Advanced Digital Signal Processing[M]. Beijing:Tsinghua University Press, 2009.
[11] 李德世,李涛. 某型超近程主动防护雷达跟踪滤波算法研究[J]. 微电子学与计算机,2010,27(11):86-90.
LI De-shi, LI Tao. The Research on Tracking Filter Algorithm of a Certain Type of Shore-Range Active Defence Radar System[J]. Micro-Electronics and Computer, 2010,27(11):86-90.
[12] 陈理凯. 轻型装甲车辆主动防护系统拦截效率研究[D]. 南京:南京理工大学,2008.
CHEN Li-kai. Interception efficiency of Active Protection System for Light Armored Vehicle [D].Nanjing: Nanjing University of Science and Technology,2008.

