Sobolev 方程的各向异性非协调Crouzeix-Raviart 型有限元分析①
李书文, 王寿城, 谢燕燕
(合肥工业大学数学学院,安徽合肥230009)
0 引言
本文主要目的针对Sobolev方程在各向异性网格下,采用混合有限元方法建立有限元子空间,讨论一个Crouzeix-Raviart型非协调线性三角形元的推广应用问题.首先构造剖分单元,建立问题的半离散混合元格式,给出离散格式的解的唯一性.其次给出相应的收敛性结果和误差估计.在研究过程中摒弃了传统的正则性假设和分析中必不可少的Ritz投影,得到了与传统有限元相同的误差估计.这表明传统有限元分析所要求的正则性网格剖分的前提条件并不是必要的,同时验证了文中采用的一类新的非协调C-R型三角形元的有效性,是对Sobolev方程研究的扩充,也是丰富了各向异性问题研究和应用.
1 单元构造


设Ω是R2中的一个有界凸多边形区域,Jh为Ω的一个三角形剖分族,但剖分不要求满足通常的正则性假设.设Jh满足文献[4]中定义的最大角条件和坐标系条件.对于任意的K∈Jh,顶点坐标为ai(xi,yi),i=1,2,3.存在可逆反射变换 FK→ K
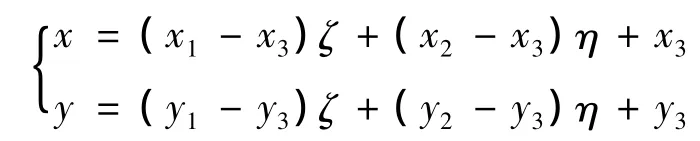
2 半离散格式误差分析
考虑的Sobolev方程如下
勘探部署方案包括井位数量、井位位置和钻井设计3部分内容。井位数量的确定要满足探明可采储量的需要;井位位置的确定要依据岩性油藏分布的特点,同时兼顾开发方案的需要;单井钻探要依据实现地质目的和降低成本的要求来设计。
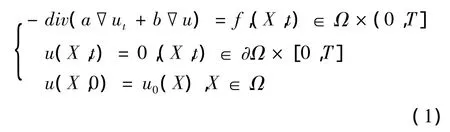
其中a=a(X,t),b=b(X,t),f=f(X,t),u0(X),f(X,t)为已知函数且|b|≤ α0,0 < α1≤a≤α2,|at|≤α3,(X,t)∈Ω × (0,T](α0,α1,α2,α3为常数,X=(x,y),a,b∈W1,∞(Ω),∀t∈(0,T],Ω为有界凸多边形区域.引入中间变量p=a▽ut+b▽u,则问题(1)的变为
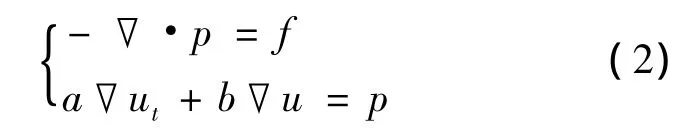
记 V=H10(Ω),M=(L2(Ω))2,∀v∈ V,w ∈M分别与式(2)中的一式和二式做内积,结合Green公式,求(u,p):(0,T]→ V × M,使得


易知▽Vh⊂Mh满足匹配关系.插值算子
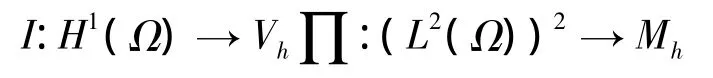
则

其中 I|K=IK,∏K=∏K. 且 ‖·‖1,h=是Vh上的模.与(3)对应的有限元逼近为:求(uh,ph):[0,T]→ Vh× Mh,使得(▽uh,▽vh)h以及(Vh,Mh)分别满足连续和离散LBB条件,易知逼近问题的解存在唯一的.

引理 在各向异性网格下,∀u,p∈H2(Ω),vh∈ Vh,有
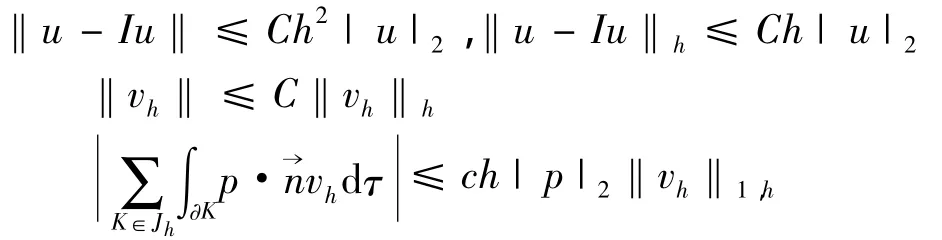
定理 设(u,p),(uh,ph)别为(3)和(4)解,u,ut∈ H2(Ω)时,则有
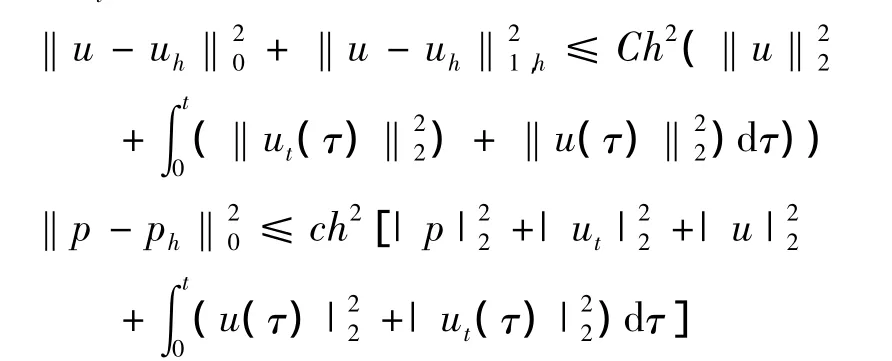
证明: 令f=0.在(4)第一方程中令vh=uht,则(p,▽uht)=0.
记

由引理, 则 有‖η‖0+h‖η‖1,h≤ch2‖u‖2.‖ρ‖0≤ ch‖p‖2.
结合(3)和(4)式得误差方程
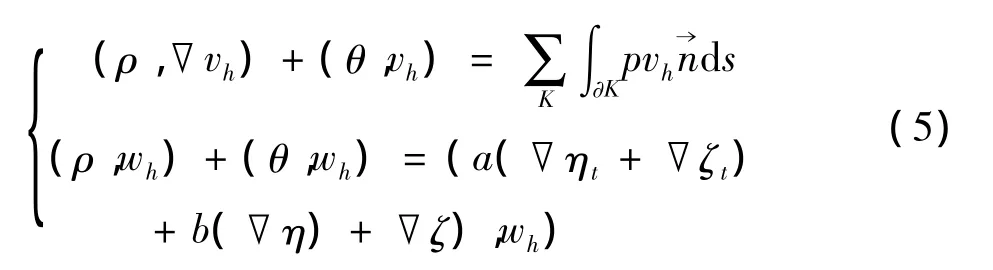
注意到▽Vh⊂Mh,在(5)第一方程中令vh=ζ,第二方程令wh=▽ζ,代入并联立可得
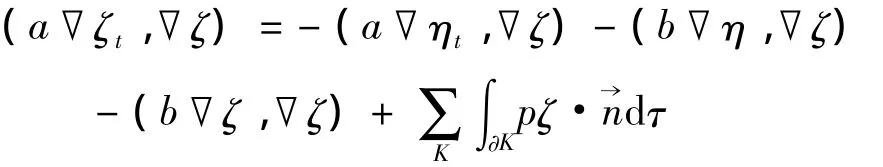
引理的三式,Cauchy不等式,Young不等式和

可得

作积分,由Gronwall引理
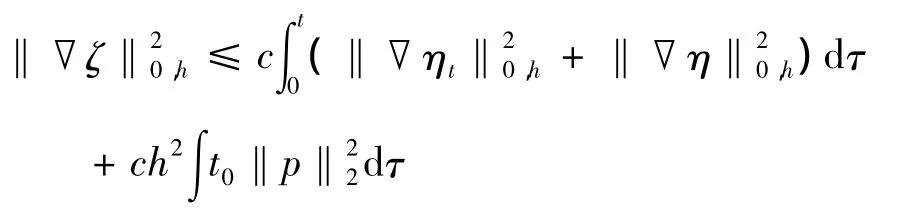
在(5)式第一、二方程中分别令vh=ζt,wh=▽ζt,则

由Cauchy不等式和引理得
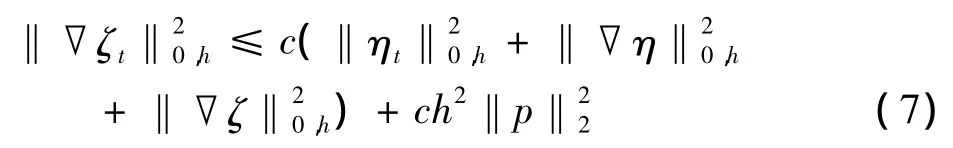
由(6),(7)得
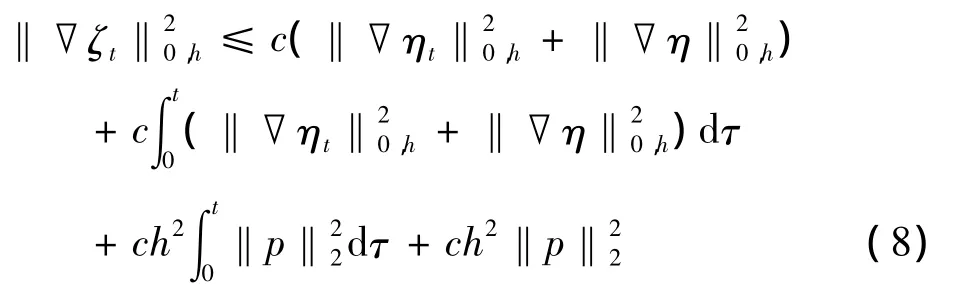
在(5)式第二方程中令wh=θ,则有

由(6)和(8)得
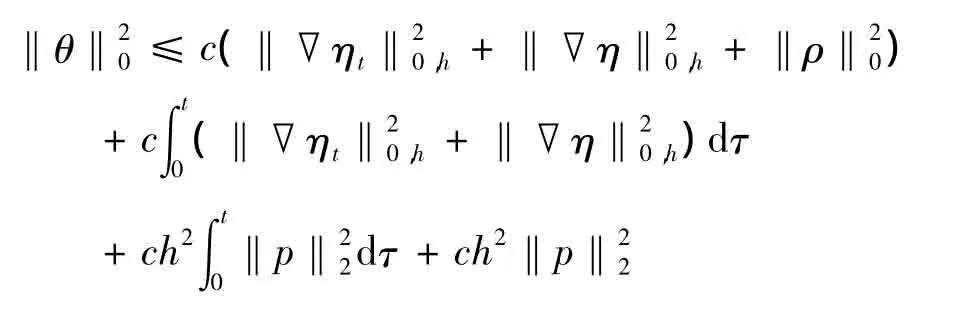


证毕.
[1] 施德明.非线性湿气迁移方程的边值问题[J].应用数学学报,1990,13(1):31 -38.
[2] 王云鹏,郭建霞.各向异性非协调混合有限元上Sobolev方程的半离散格式及误差估计[J].新乡学院学报:自然科学版,2011,28(5):408 -410.
[3] 郭玲,陈焕贞.Sobolev方程的H1-Galerkin混合有限元方法[J].系统科学与数学,2006,26(3):301 -314.
[4] 石东洋,许超.二阶椭圆问题的各向异性非协调Crouzeix-Raviart型有限元方法[J].应用数学和力学,2012,33(2):240-249.
[5] 张亚东,石东洋.各向异性网格下抛物方程一个新的非协调混合元收敛性分析[J].计算数学,2013,35(2):171 -180.
[6] 马戈,丁伟.抛物方程各向异性非协调逼近和数值模拟[J].南阳理工学院学报,2011,3(6):112 -116.
[7] 石东洋,汪松玉,陈绍春.两类各向异性非协调元的某些超收敛性质分析[J].计算数学,2007,29(3):263 -272.
[8] 石东洋,王慧敏.Stokes型积分微分方程的质量集中各向异性非协调你有限元分析[J].应用数学,2009,22(1):33 -41.
[9] 陈红晓,刘晓奇,徐大.粘弹性双曲型方程的H1-Galerkin混合有限元方法[J].高等学校计算数学学报,2011,33(3):279-288.
[10] 石东洋,李志燕.二阶椭圆问题的非协调混合元收敛性分析[J].河南师范大学学报:自然科学版,2008,36(4):1 -3.

