二项分布参数的经典估计与Bayes 估计相等的关系①
2014-07-09 02:00:00姚丽
佳木斯大学学报(自然科学版) 2014年4期
姚 丽
(吉林师范大学数学学院,吉林四平136000)
0 引言
文献[2]中称“贝叶斯学派至今尚未证明总体分布p(x/θ)中的参数的任一经典估计都存在一个先验分布,使得其贝叶斯估计就是该经典估计”,这一命题现在仍未解决.
由于二项分布是实际中常用的离散分布,并且最大似然估计和矩估计是主要的参数估计方法,为此,以二项分布为研究对象来探讨命题真伪对于最终解决问题是有益的.本文证明了二项分布中未知参数的经典估计(最大似然估计和矩估计),一定存在一个先验分布,使其贝叶斯估计就是该参数的经典估计的结论.
1 二项分布中未知参数的经典估计
1.1 最大似然估计
从总体X中抽取简单随机样本X1,X2,…,Xn,得到x1,x2,…,xn,则二项分布中样本的似然函数:

对数似然函数:

令
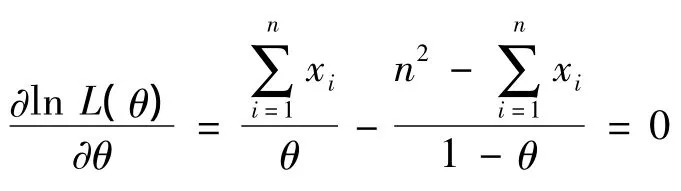
则

1.2 矩估计
2 二项分布的后验分布
我们取贝塔分布Be(α,β)作为二项分布中未知参数θ的先验分布,其中,α和β已知,则

未知参数θ的后验分布

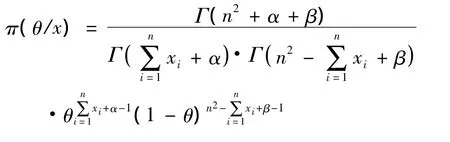
3 二项分布中未知参数θ在取Be(α,β)下的 Bayes估计
由文献[3]知,二项分布中未知参数在取先验分布Be(α,β)下的Bayes估计B=E(θ/x),由于
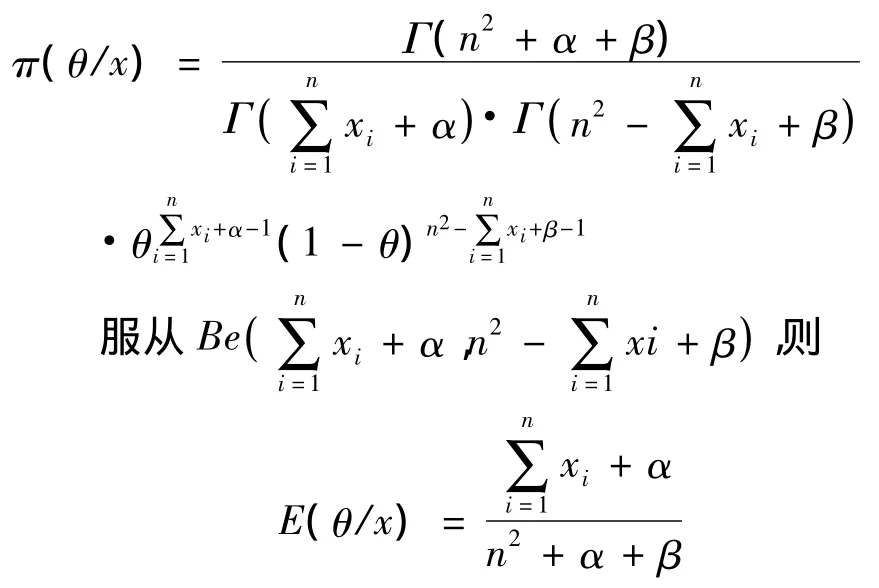
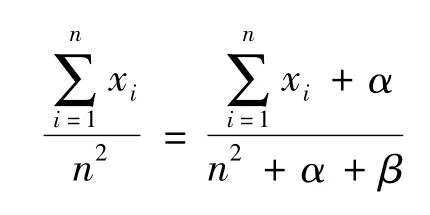

4 结 论
本文以二项分布为例,讨论并证明了其未知参数θ的经典估计(最大似然估计和矩估计)都存在一个先验分布 Be(α,β)(α 和 β 满足条件:β =),使得其贝叶斯估计就是该经典估计,这一结论的确定有利于继续研究贝叶斯统计中未解决的问题.
[1] 彭燕.贝叶斯估计和经典估计的对比研究[J].岳阳师范学院学报(自然科学版),2002,15(01):1008 -620X.
[2] 茆诗松.贝叶斯统计[M].北京:中国统计出版社,1999.
[3] 张尧庭,陈汉峰.贝叶斯统计推断[M].北京:科学出版社,1991.
[4] 茆诗松,王静龙,濮晓龙.高等数理统计[M].北京:高等教育出版社,2006.
[5] 茆诗松,程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2008.
猜你喜欢
机械设计与研究(2023年5期)2023-11-01 07:17:32
机械设计与研究(2023年3期)2023-09-19 02:11:40
机械设计与研究(2023年2期)2023-07-25 11:05:56
中学生数理化(高中版.高二数学)(2022年5期)2022-06-01 06:26:58
中学生数理化(高中版.高考数学)(2021年3期)2021-06-09 06:09:10
中学生数理化(高中版.高考数学)(2021年3期)2021-06-09 06:09:08
工程数学学报(2020年3期)2020-07-06 07:38:40
长治学院学报(2019年2期)2019-07-24 07:14:04
校园英语·中旬(2017年9期)2017-09-06 00:55:24
贺州学院学报(2017年1期)2017-06-05 09:15:36

