燃烧器内气固两相流动的分区并行计算

符栋良

（上海市特种设备监督检验技术研究院）

工程上有许多装置都很庞大，有的还处于高温、高压甚至有害的环境下工作，因此要进行有关的实验往往很困难，甚至是不太现实的。于是我们就用数值模拟，即用数学的方法模拟实际问题。随着计算机存储容量的不断增加，计算速度的不断提高，计算方法的不断完善，数值模拟得到了迅速的发展。然而对大规模问题进行数值模拟往往还需要消耗大量的计算机资源，所以有必要用多机来进行并行求解以提高计算效率。

气固两相流动广泛存在于各种分离和燃烧装置中，正确预报其中两相速度、颗粒浓度及两相湍动能分布，对了解流动、混合及反应机理，进行优化设计以提高性能，都很重要。火力发电厂燃烧器中空气和煤粉混合物的流动就是典型的多相流动工况[1]。其计算规模很大，加之其计算区域比较复杂，所以对并行计算更是有迫切的需求。

1 区域分解法

区域分解法[2]是把计算区域分解为若干个子区域，子区域应尽可能规则，从而将原问题的求解转化为在子域上的求解。它把大问题化为若干个小问题，从而缩小了计算规模。这对于克服计算机容量和速度的限制具有极大的意义。本论文正是基于这一想法，决定采用区域分解算法，实现对燃烧器一次风喷咀和弯头组件内气固两相流动问题的分区并行求解。根据区域分解理论，各子区域划分好以后，关键的问题是子区域之间交界面上的信息如何进行快速有效的传递，保证计算的收敛性。这也就是所谓的交界面技术 （interface method）。

交界面技术包括两大类，即非重叠区域耦合和重叠区域耦合。前者具有简单方便的优点，但是应用范围不够广。后者应用范围广，但是一般要求耦合区域具有相同的网格系统且不得划分更多的子区域，这对于复杂区域来说显得不够灵活。本文所采用的是非重叠区域分解算法。根据区域分解的思想和算法，将计算区域进行合理的划分，可以实现分区计算。若进一步结合并行技术，则可利用现有的微机资源，在微机网络上实现较大规模问题的分区并行计算

2 并行计算环境

2.1 MPI介绍

本文采用的网络并行环境是MPI(message passing interface)，MPI是目前最重要的实现消息传递的并行编程环境之一，它具有移植性好、功能强大、效率高等多种优点[3]。具体地讲，MPI就是提供了并行库。这样，原来的串行编译器能够继续使用，编程者只需要在原来的串行程序中加入对并行库的调用，就可以实现并行程序设计。

一个典型的基于MPI并行环境的程序框架结构可以用图1来表示。

图1 MPI程序的框架结构

2.2 MPI并行程序的主从模式

MPI的两种最基本的并行程序设计模式是主从模式和对等模式。本文所选用的是主从模式，这种计算模式有一个控制程序称为主进程，负责进程的生成、发送、收集数据并显示计算结果，其余的从进程执行实际计算，如图2所示。

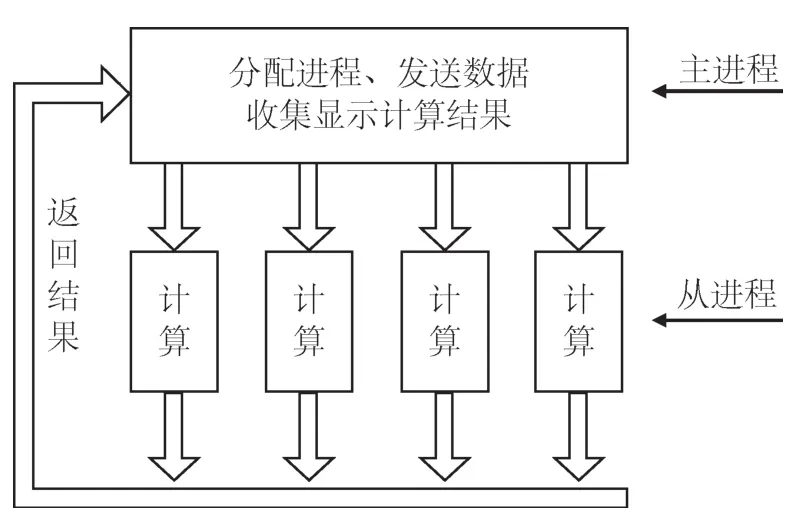
图2 并行计算主从模式的流程

可以说，服务器提供服务的软件或进程，而客户机则接受服务的软件或进程。服务器和客户机是针对网络的通信进程而言的，不是针对网络客户或个人计算机的。区分服务器和客户机主要取决于通信进程双方的地位。同一台个人计算机，用户设置不同的进程，那么用户可能既是某个进程的客户机，又是另一个进程的服务器。

主从模式具有以下两个优点。

（1）主从模型可以应付网络中资源、运算能力和信息的不均等现象。

主从模式的最重要的特点是非对等的相互作用，即主进程和从进程处于不平等的地位。服务器拥有客户机所不具备的硬件、软件资源和运算能力，服务器提供服务，客户机请求服务。同时，网络中还存在人为的不均等现象。这种不均等主要是指信息而言，例如为节约网络资源没有必要在每台机上都保存一个拷贝，特别是在科学计算中存在的动态变化信息，如果每台主机都保存一份拷贝，那么为保持所有拷贝的一致性，要进行的动态修改和刷新工作，其开销是非常巨大的。

（2）主从模式可以使数据交换保持同步。

网络通信不同于单个计算机之间的通信的一个特点是，网络通信是完全异步的，相互通信之间既不是父子关系，也不共享内存缓冲区。因此需要一种机制，为准备通信的进程之间建立联系，使二者的数据交换保持同步。而主从模型解决了上述问题。在主从模式中，每次通信均由随机启动的从进程发出，主进程一直处于等待状态。这样可以保证主进程随时对从进程请求做出响应。

3 燃烧器的物理模型

本文的研究对象是贵州某电厂300 MW机组中的锅炉用燃烧器，即1025 t/h亚临界压力无烟煤锅炉中使用的一种新型燃烧器。

这是一个四角切圆直流燃烧器，和一般燃烧器相比，新型燃烧器在燃烧器一次风喷咀靠近出口处增加了一个菱形的障碍块，其目的是使燃烧器出口煤粉较均匀。携带着煤粉的一次风从垂直圆管的下部进入燃烧器，从水平方管的右侧出口喷入炉膛。管道除了垂直圆管和水平方管外，还有两个弯曲段和一个圆管变方管过渡段。第一个弯曲段为45°，位于Y-Z平面上；第二个弯曲段为90°，是在与垂直平面和水平面都成45°的平面上。圆管直径为426 mm，方管尺寸为宽580 mm、高406 mm。具体结构如图3所示。

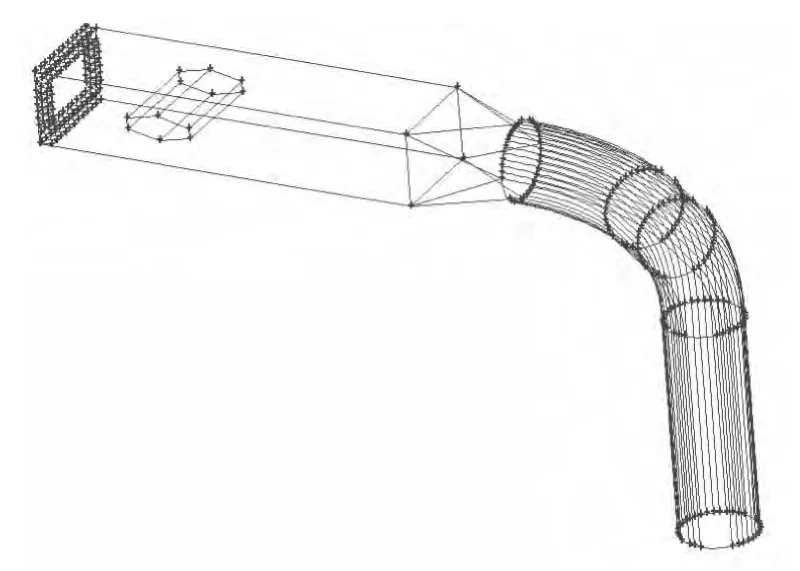
图3 带有菱形体的一次风喷嘴及弯头组件

4 计算网格生成

燃烧器组件网格生成的整体思路是采用多块技术，将物理域划分成多个子域，在每个子域中利用贴体网格技术中的解椭圆形方程的方法生成结构化网格。为了保证网格质量，块与块交界面上的网格保持一致[4]。

在区域分解中，将整个计算区域分裂为六个子域Ωt，从入口到出口其名称和网格规模依次为：第一部分 （包括垂直圆柱、90°弯管部分、圆管变方管的过渡段）65 mm×16 mm×16 mm、方管部分20 mm×16 mm×16 mm、菱形障碍块的上部10 mm×16 mm×6 mm、菱形障碍块的下部10 mm×16 mm×6 mm、出口部分的方管10 mm×16 mm×16 mm和出口后的大空间 100 mm×100 mm×100 mm。 ∂Ωt(t=1，2，3，4，5，6)为其边界，∂Ω 为整个计算区域的边界。图4是燃烧器一次风组件整体的网格分布图。其中在数值模拟中用到的炉膛部分的网格图未给出，仅给出燃烧器一次风组件内的网格图。

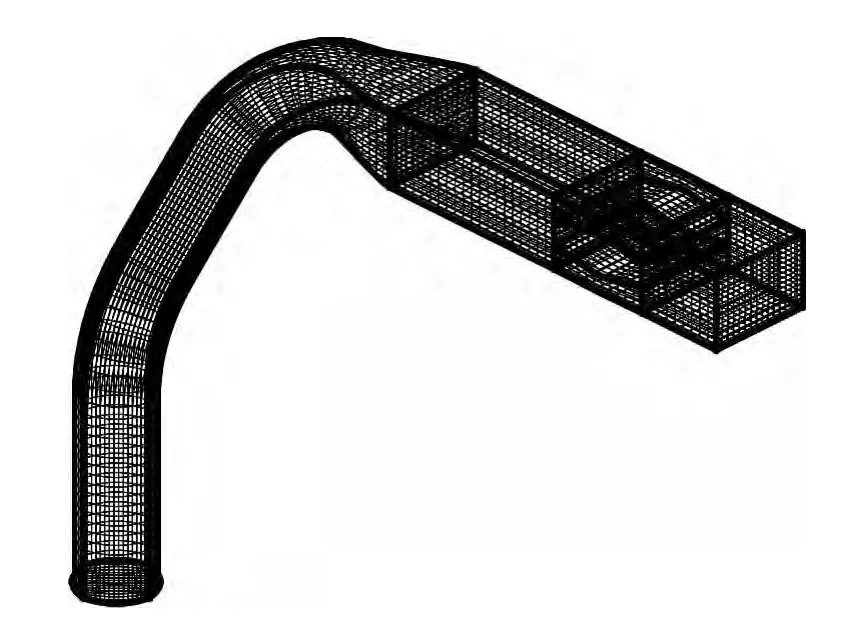
图4 燃烧器一次风组件整体的网格分布图

5 气固两相湍流数值解法

本文选择单流体模型来模拟燃烧器一次风喷咀及弯头组件内的气固两相流动。

本文对气固两相流动采用单向耦合[5-8]。颗粒相的求解是建立在气相场得到粗收敛解的基础上的。颗粒相的压力近似取为气相场的压力；对于颗粒相的速度场和密度场，用幂函数差分法对固相动量方程和连续性方程进行离散，得到关于速度场和浓度场的代数方程组，然后耦合迭代求解，最终得到满足颗粒相动量方程和连续性方程的密度分布和速度分布。

6 并行方案

区域分解方法是一类适合于分区并行处理的偏微分方程数值求解的方法。它的基本思想就是，把物理问题的求解区域按照一定的原则 （如几何形状、物理特性等）分解成若干个相对简单的子区域，于是原问题的求解就转化为在各子区域上的分别求解及各子区域之间的边界耦合。

根据主从模式的特点，我们可以安排每个从进程 （一台客户机运行1至2个从进程）负责一个子区域的计算。从进程在迭代若干步后，首先要把一些相关的交界面信息传给主进程，然后主进程会根据条件得到新一轮的交界面信息，最后再把这些新得到的信息传给相关的从进程。有关详情可参照文献 [9]～文献 [15]。

本文对于燃烧器一次风喷咀和弯头组件内的三维气固两相流动问题使用5台PC机并行求解，其中1台PC机作为服务器运行主进程，另外4台作为客户机运行从进程。这5台机器的软硬件配置如下。

服务器： CPU，AMD 64×2 Dual； 内存，1G；操作系统，Windows XP。

客户机 1： CPU， AMD 64×2 Dual； 内存， 1G；操作系统，Windows XP。

客户机 2： CPU， AMD 64×2 Dual； 内存， 1G；操作系统，Windows XP。

客户机 3： CPU， AMD 64×2 Dual； 内存， 1G；操作系统，Windows XP。

客户机 4： CPU， AMD 64×2 Dual； 内存， 1G；操作系统，Windows XP。

本文将整个燃烧器计算区域分成6个子块，如图4所示。每一块即在计算过程中对应于一个进程。其中进程1放在客户机1上，进程2、3放在客户机2上，进程4、5放在客户机3上，进程6放在客户机4上。

这里的服务器主要负责交界面信息的耦合、数据转发和判断收敛等工作，而客户机主要负责各计算区域边界、入口和出口条件的初始化以及对一个（或多个）子区域的数值求解工作。图5给出了服务器与客户机的关系图。其中S代表服务器，C1、C2、C3和C4代表4个客户机，箭头代表数据传递的方向。

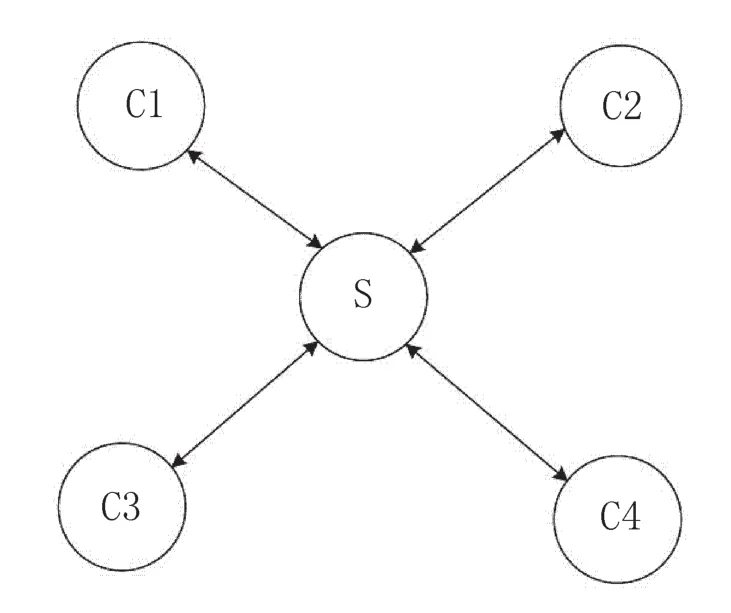
图5 服务器与客户机关系

7 数值模拟结果及分析

以下对Re=105时燃烧器一次风喷咀和弯头组

件内的气固两相流动的速度、湍动能、颗粒相浓度和并行效率等参数进行分析。

7.1 流场分析

流体流经菱形障碍块后，同样也会在障碍块后方形成两个尾涡区。需要指出，该尾涡区是有利于炉膛内稳定燃烧的。颗粒速度分布如图6所示。

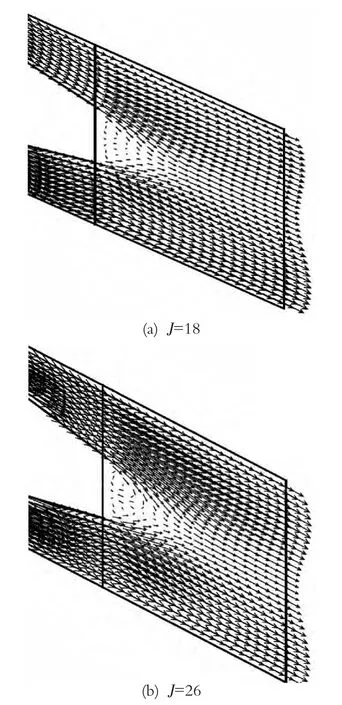
图6 J平面的颗粒速度分布

7.2 整流现象

图7为燃烧器一次风喷咀水平管内横向截面的气相速度矢量图。图7中y+为水平管轴线方向的无量纲化的刻度 （y+=y/din，y为水平管轴线方向的刻度，din为入口圆管的直径）。

其具体代表的物理位置为：

y+=2.15—— 圆管第二次弯曲后的截面；

y+=3.00——圆管变方管过渡段的截面；

y+=4.65——水平管内靠近菱形障碍块前端的截面；

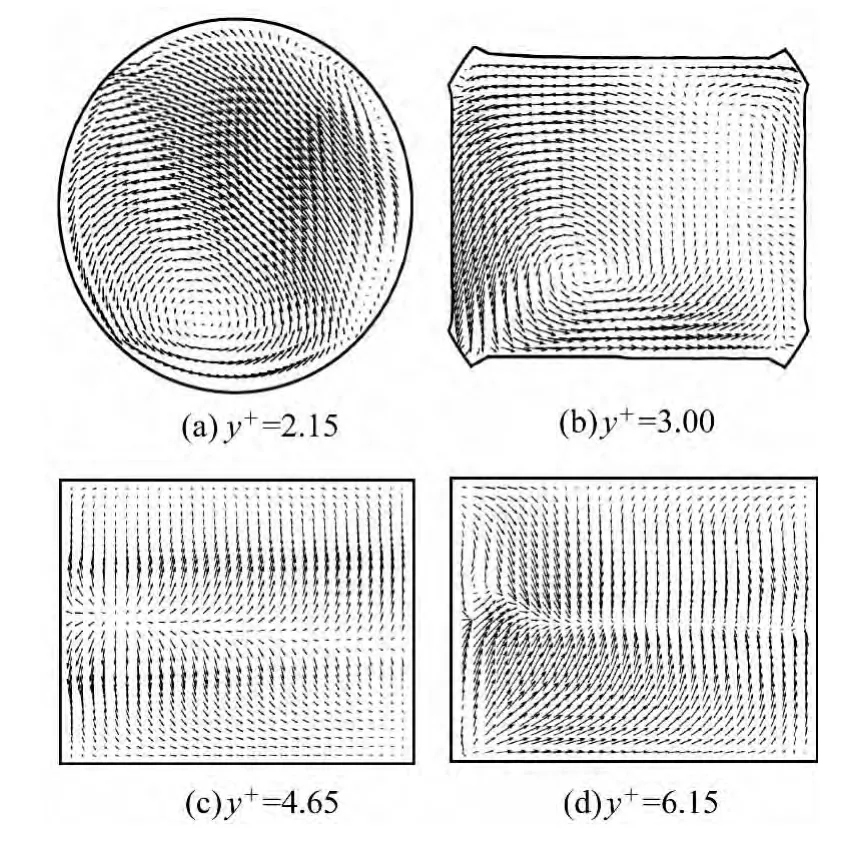
图7 燃烧器内横向截面的气体速度矢量图

y+=6.15——水平管内靠近菱形障碍块后端的截面。

从图7可以看到，当流体从垂直管道经过弯头流入水平管道时，由于管道需要为流动提供向心力而产生横向压差，从而导致流场在经过弯头后出现双螺旋流现象，这就是所谓的 “弯头效应”。此外，类似于 “后向台阶效应”，经过弯头的流动会在内侧产生一定程度的分离并形成一个尺度较大的回流区，从而导致轴向速度沿横向截面的分布很不对称。然而，由于菱形障碍块的存在，它有一定的整流作用，所以当遇到障碍块的时候，螺旋流现象得到消除，并且通过障碍块后的流动也变得上下比较对称了。

7.3 湍动能分析

图8为燃烧器一次风喷咀水平管内障碍块前后的Y-Z平面的湍动能分布图。

其中的湍动能为无量纲湍动能，其定义为k+=k/u2in，其中k代表实际的湍动能，uin代表实际的气体入口速度。x+为水平管径向的无量纲化的刻度（x+=x/din，x为燃烧器水平管水平径向的刻度，din为入口圆管的直径）。

从图8可以看出，由于障碍块的出现，使得流场受到干扰，从而障碍块前后的湍动能有明显的提高。

7.4 浓度场分析

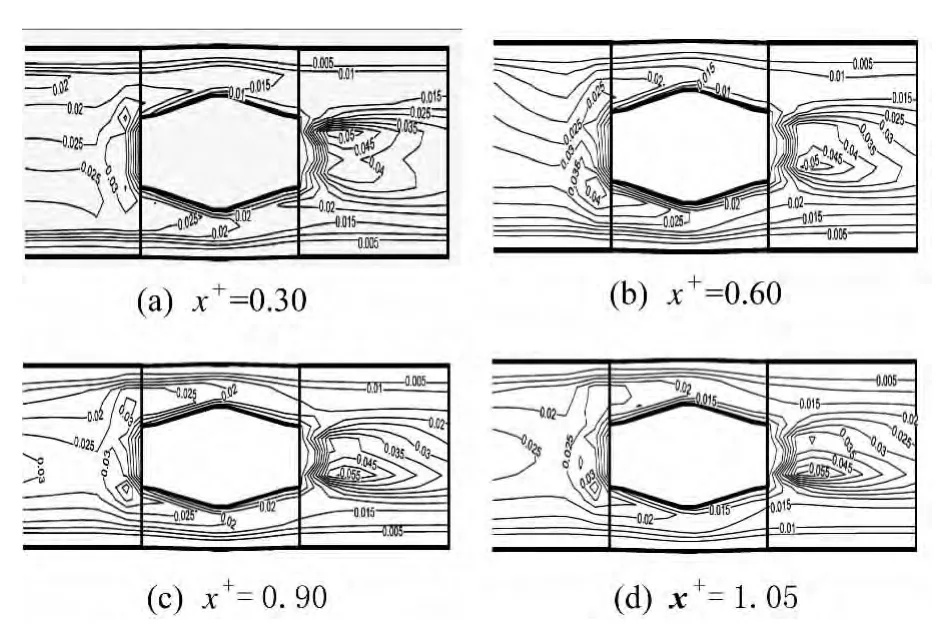
图8 燃烧器内障碍块前后Y-Z平面的湍动能分布

图9为燃烧器一次风喷咀近出口处Y-Z平面内的颗粒相浓度分布图。图9中的浓度值为无量纲值，其定义为nk+=nk/nkin，其中nk为实际颗粒相的浓度，nkin为实际颗粒相的入口浓度。x+为燃烧器一次风喷咀水平管水平径向的无量纲化的刻度 （x+=x/din，x为水平管水平径向的刻度，din为入口圆管的直径）。

从图9我们明显可以看出，由于受到障碍块阻挡，煤粉在障碍块前有堆积，所以浓度较高；由于该菱形障碍块的布置位置离弯头较远，所以不能起到浓淡分离的作用。

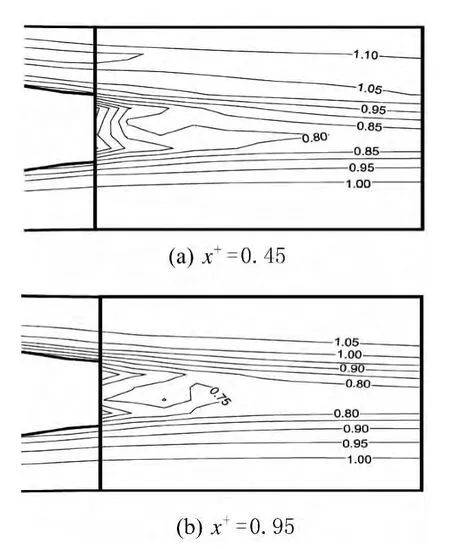
图9 燃烧器一次风喷咀近出口处Y-Z平面的颗粒相浓度分布

7.5 并行性能分析

下文从并行计算的并行执行时间、加速比和并行效率上来进行并行性能的分析。

其计算公式如下：

式中Sn——加速比，衡量并行机群有多快；

t1——顺序执行时间，即程序在单处理机上的运行时间；

tn——并行执行时间，即程序在并行机群上的运行时间；

En——并行效率，衡量处理机的利用率；

n——处理器的数目。

表1列出了使用单机求解和多机并行求解该问题的并行性能参数。其中多机求解是指在5台PC机上运行分区并行算法，而单机求解是指在客户机1上运行该算法。从中我们可以明显看出，使用区域分解法在MPI环境下并行求解燃烧器内气固两相流动问题有较高的加速比和并行效率。特别是其计算时间要低于同规模问题的单机串行计算时间约115 h，这在数值计算中是比较可观的时间，可见在MPI并行平台上对大型复杂问题进行并行的数值求解有着很好的价值和前景。

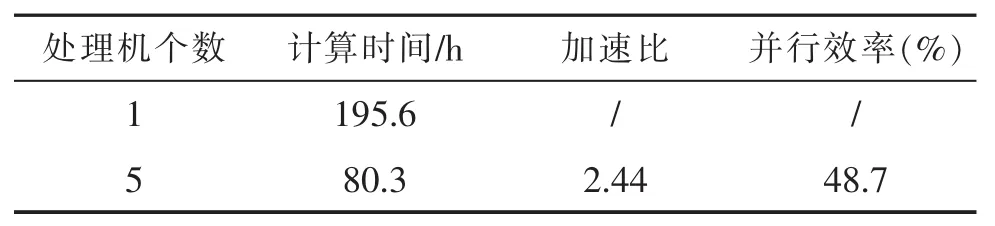
表1 燃烧器内分区并行计算并行效率

8 总结

本文在PC机群上通过MPI软件包建立起了网络并行计算平台，并在此基础上采用区域分解法对燃烧器一次风喷咀和弯头组件内气固两相冷态流动问题进行了并行的数值求解。

本文的工作具体来说具有以下几点意义：

(1)证实了在普通PC机集群上开展并行计算的可行性。

(2)本文自行开发出一套程序来模拟燃烧器一次风喷咀和弯头组件内的气固两相流动，正确预报其中两相的速度、颗粒浓度及湍动能分布。对于燃烧器结构的改进有一定的指导意义，也为以后进行炉膛内的数值模拟提供更加准确可靠的边界条件。

(3)通过区域分解方法实现分区并行求解，既减少了计算工作量，也提高了代数计算的品质。

(4)在MPI并行平台上成功实现对三维复杂流动问题的并行求解，再一次证明了该并行算法具有良好、可靠和高效的工作性能。

(5)本文中所开发的基于MPI并行平台的计算程序具有良好的数据通讯性和程序通用性，这为将来并行程序的模块化打下了基础。

总的说来，本论文的结果是符合流体力学的基本规律和实际情况的，使用区域分解的并行算法对模拟燃烧器一次风喷咀和弯头组件内气固两相流问题也具有较高的效率。所以本文的工作对于在一般PC机集群上并行求解大规模复杂流动问题是非常有参考和指导价值的。计算机数值模拟总是在朝着更高的计算精度、更好的区域适应性和更强的健壮性方向发展。在计算机技术高速发展的今天，数值模拟对工程实际具有很重要的指导意义。

[1]冯俊凯，沈幼庭.锅炉原理及计算 [M].第2版.北京:科学出版社，1992.

[2]吕涛，石济民，林振宝.区域分解算法——偏微分方程数值解新技术 [M].北京:科学出版社，1997.

[3]郁志辉.高性能计算并行编程技术 [M].北京：清华大学出版社，2001.

[4]陆霄露.基于PC网络求解复杂三维流动的分区并行方法 [D].上海:上海交通大学，2003.

[5]陶文铨.计算传热学的近代进展 [M].北京：科学出版社，2000.

[6]Patankar S V.郭宽良译.传热和流体流动的数值方法[M].北京:科学出版社,1984.

[7]蒲砢.关于气固两相流数值计算模型的探讨 [J].重庆建筑高等专科学校学报，2000,10(4).

[8]周力行.湍流气粒两相流动和燃烧的理论与数值模拟[M].北京：科学出版社，1994.

[9]陈国良.并行计算——结构·算法·编程[M].北京:高等教育出版社，1999.

[10]陈国良.并行算法的设计和分析 [M].第2版.北京：高等教育出版社，2002.

[11]王小伟，郭力，唐德翔,等.两相体系宏观拟颗粒模拟并行算法 [J].化工学报，2004，55(5)：716-720.

[12]吕雄伟.基于网络的循环流化床锅炉整体数学模型的分布式算法研究 [D].重庆:重庆大学，2001.

[13]Brakkee E A,Segal A,Kassels C G M.A parallel domain decomposition algorithm for the incompressible Navier-Stokes equations[J].Simulation Practice and Theory,1995(3):363-389.

[14]吕晓斌，兰黔章，朱自强.求解Euler方程的区域分解方法与并行算法[J].计算物理，2000，17(4)：360-366.

[15]王开春，李树民，朱国林.三维低速NS方程的并行计算 [J].空气动力学学报，2002，20：88-93.