终端区航迹簇的中心航迹提取方法研究

赵元棣 ， 孙 禾， 王洁宁， 李 桃

（1. 中国民航大学天津市空管运行规划与安全技术重点实验室，天津 300300；2. 中国民航大学空中交通管理研究基地，天津 300300；3. 中国民航大学图书馆，天津 300300）

终端区空域系统是整个空管系统中情况最为复杂的子系统之一，它是航空器从进离场阶段到航路飞行阶段的过渡区域。在终端区内，每个航班均按照预先制定的飞行计划中的标准进离场航线飞行。所谓飞行计划，是指航空公司在航班飞行之前，根据气象条件、航行情报、飞机性能及运载重量等情况通过计算所制定的标准飞行航线、高度和飞行时间等。然而，在实际运行中，会有诸多因素（如：实时气象环境、终端区容量、交通管制服务等）影响航空器的飞行，导致实际飞行航迹与飞行计划所制定的标准航线有所偏差。随着空中交通流量的不断增加，终端区内的飞行状况日益复杂，给管制员的现场指挥带来了巨大的挑战。因此，研究航班的历史飞行航迹簇，提取具有代表性的中心航迹并识别、分析其特征，计算其与飞行计划航迹的偏差，对于航空公司制定同一航班在未来的飞行计划具有重要的意义，减小了该航班在未来飞行中出现偏差的可能性，从而有效减轻管制员的工作负荷。

雷达监视是记录航空器历史飞行航迹的一种重要手段，它利用无线电波发现目标，准确获取航空器实时的位置、高度、航向等信息。雷达的扫描周期一般为3～5 s，因此利用雷达设备获取的航空器飞行航迹是一些具有时序的离散点集；对于同一航班的历史航迹簇，从几何的角度可以看作是一个在机场坐标系下的三维离散点云集合，可以通过数学的方法对其进行计算与分析。

计算几何是一门利用计算机研究数据处理和几何特征的学科，目前已广泛应用于各种领域。近些年，已有大量学者成功地将计算几何引入民航领域[1-3]；针对其中的航迹簇聚类与分析问题，目前大多都是基于智能计算的方法[4-6]，而且得到的结果大多是二维的，在实际应用中具有一定的局限性。骨架提取是计算几何中的基础算法之一，已广泛应用于模型分割[7-8]、目标匹配和检索[9-11]以及曲线曲面重建[12-14]等领域。本文针对历史飞行航迹簇，采用骨架提取的方法，提取其中心航迹曲线，并在此基础上利用平均航向和飞行高度识别其特征点。首先将历史飞行航迹簇转化为三维点云模型，接着沿飞行方向进行自适应采样得到代表点集合，随后利用代表点的航向信息建立图结构并进行优化得到点云模型的骨架曲线，最后通过均匀化处理以及光滑处理生成最终的中心航迹曲线。本文通过对某终端区的多条历史航迹簇真实数据进行实验与分析，验证了该方法的准确性、有效性和鲁棒性。

1 终端区航迹簇的中心航迹提取方法

1.1 航迹簇生成点云模型

由雷达设备接收到的某终端区飞行航迹数据如图1所示，其中每行数据均包括：接收时间、航班号、机场坐标系下X坐标和Y坐标、飞行高度、速度、航向角等信息。由于本文是采用计算几何方法对雷达数据进行处理，故只需针对同一航班在不同日期的飞行航迹提取其几何相关信息，即：以机场归航雷达为原点建立的机场坐标系系下的X坐标和Y坐标，单位为千米(km)；飞行高度，单位为米(m)；以及飞行航向角，单位为度，如图1中红框部分所示。

图1 雷达监视数据

按照接收时间的顺序将上述数据可视化，可以得到同一航班的飞行航迹簇，如图2(a)所示，其中每条曲线均代表一条飞行航迹。进一步，如果忽略其时序特征，即可得到飞行航迹簇的三维点云模型P，如图2(b)所示。需要说明的是，由于进离场航空器的飞行航迹沿Y轴跨度较大，因此出于美观的考虑，本文插图均采用非等比例坐标轴。

1.2 沿飞行方向采样

由于航空器在终端区内最理想的飞行航迹就是飞行计划中所制定的标准进离场航线，所以由航迹簇生成的三维点云是与标准航线具有相似拓扑结构的“管状”、“无自交”点云模型；此外，航空器在进离场时速度随飞行高度降低而减小，导致在雷达扫描间隔固定的前提下，三维点云模型具有多尺度的特点，即：越靠近X-Y平面的点云密度越大。对于上述多尺度、无自交的三维点云 P，本文采用文献[14]中的方法对其进行自适应采样，具体算法如图3所示。

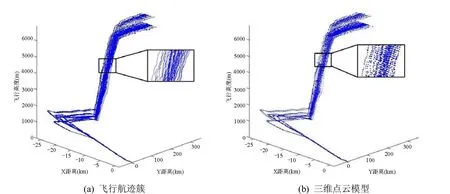
图2 飞行航迹簇及三维点云模型

图3 自适应采样流程图

其中Rmin和Rmax为事先给定的阈值。由于航迹簇生成的点云模型在局部大多具有线性结构，因此上述方法使采样过程沿着线性伸展区域，即航空器飞行方向进行，从而大大提高了采样效率。由此方法得到的三维采样结点集Q在较好地保持了原始点云模型拓扑结构和几何特征的基础上，大幅度地减少了三维离散点的数量，如图4所示。

图4 沿飞行方向采样结果

1.3 图的建立与优化

利用上述方法得到的每个采样结点qi∈ Q ， 均代表了原始点云模型中的一个子集Pi⊂ P ，且满足∪ Pi=P 和 Pi∩Pk= φ，∀i≠k。为了准确表现原始三维点云模型的拓扑结构，我们在采样结点集Q上利用其航向信息建立图G：对于两个采样结点qi,qk∈Q ，当它们所对应的原始点云集合Pi和Pk的 K近邻中含有相同的点，且它们的航向角 hi与hk变化不大（小于给定的阈值）时，则在它们之间建立一条边。其中，采样结点的航向角设为其代表点集中点的航向角的平均值。对于采样结点集中的每两个结点均采取如上操作，即可得到近似反映原始航迹簇形状的图G，如图5所示。在终端区中，进场航空器在切入五边进近时的航向角差别较大，因此利用上述方法建立的图可以避免由于航迹点空间位置相距较近而引起的错误连接。

图5 图G的建立

由图5可以看出，图G虽然近似还原出了原始航迹簇的拓扑结构，但是在局部含有环结构，不符合飞行航迹的无自交特性，因此接下来利用退化算子对图G进行优化操作：对于图G中的环Ci，计算其几何中心作为新的结点代替该环，并更新与环Ci相连的边集以及其代表点集，如图6(a)所示。为了在保持图G的拓扑结构的同时，使图G的几何特征更逼近于原始点云模型P，我们从含有度为2的结点的环开始应用退化算子，直至删除图G中所有的环结构为止。

图6 图G的优化

在应用退化算子进行优化操作后，图G已经成为一条曲线，如图6(b～c)所示。然而，在环结构的退化过程中，可能会产生一些多余的短边，我们利用事先给定的边长阈值对这样的短边进行识别并删除它们，从而得到一条既能准确反映原始航迹簇的拓扑结构，又能近似表示其几何特征的中心航迹曲线。

1.4 中心航迹的均匀化处理与光滑处理

一般来讲，由上述方法得到的中心航迹曲线的边长并不均匀，尤其是在环结构密集的地方（例如航迹转弯处），我们对其进行均匀化处理，即：在长边上插入新的采样结点，将其均匀分割成若干短边；将若干短边合并成为长边，并更新其所代表的点集。此外，由于受航空器性能及空气动力学限制，航空器在转弯时的飞行航迹较为光滑，因此我们利用Laplace算子对中心航迹曲线进行光滑处理，使其在几何上更逼近原始三维点云模型，具体优化能量函数为：

其中，L为图G所对应的Laplace矩阵，qi′为采样点qi所代表点集的几何中心。经过光滑处理后的曲线即为最终的中心航迹曲线，如图7所示。需要说明的是，中心航迹曲线上的点看似分布不均是由非等比例坐标轴所致。

2 实验结果

2.1 中心航迹提取结果

本文采集到某航班2个月共60天的进场雷达航迹数据，除去非正常进近的8条航迹，共有52条正常进近的飞行航迹形成航迹簇，应用本文方法提取其中心航迹。在实验中，我们设定参数其中d表示原始点云中每个点与其邻居点距离的平均值。

图8(a～b)所示为由上述数据中 25天和 52天的航迹簇生成的三维点云模型，以及提取得到的中心航迹曲线；图 8(c～d)所示为该终端区另一航班的飞行航迹簇及与之对应的中心航迹，可以看到本文方法无论是对于小规模的航迹簇（图8(a)14380个点，图8(c)11211个点），还是对于大规模的航迹簇（图8(b) 27681个点，图8(d)27226个点），均可以有效提取出中心航迹。

需要说明的是，中心航迹在转弯点的转弯半径与航迹簇中不同航迹的转弯半径分布有关：转弯半径分布得越分散，中心航迹的转弯半径越小。这是由于本文方法在采样过程中是将采样球中点集的重心作为采样点，而重心的位置依赖于采样球中点集的分布。因此，本文方法对于转弯半径分布密集的航迹簇效果更佳，如图 8(c～d)。

此外，对于大规模的航迹簇，可以通过增大采样半径的方法提高计算效率。图9所示为针对同一个航迹簇，利用不同采样半径进行采样，进而提取出的中心航迹曲线。可以看到本文方法对于采样半径不敏感，具有一定的鲁棒性。

图9 利用不同采样半径的中心航迹提取

2.2 基于中心航迹的特征点识别

由本文方法得到的中心航迹曲线中的每一个采样点均代表原始点云的一个子集，因此可进一步计算其平均航向角和平均速度：

其中，ih和vi分别表示原始三维离散点的航向角和速度， c ard ( Pi)表示点集 Pi的元素个数。

飞行航迹的特征点包括航向转换点、速度转换点、高度转换点等[15]，它们是4D航迹规划与预测等多个问题的研究基础。利用本文方法求得的中心航迹在具有几何位置信息（X坐标、Y坐标和飞行高度）的同时，还可以利用上述方法求得其航向角和飞行速度，从而通过计算它们之间的变化，识别中心航迹上的特征点，图 10所示为利用中心航迹识别出的高度转换点（黑色五角星）和航向转换点（粉色五角星）。

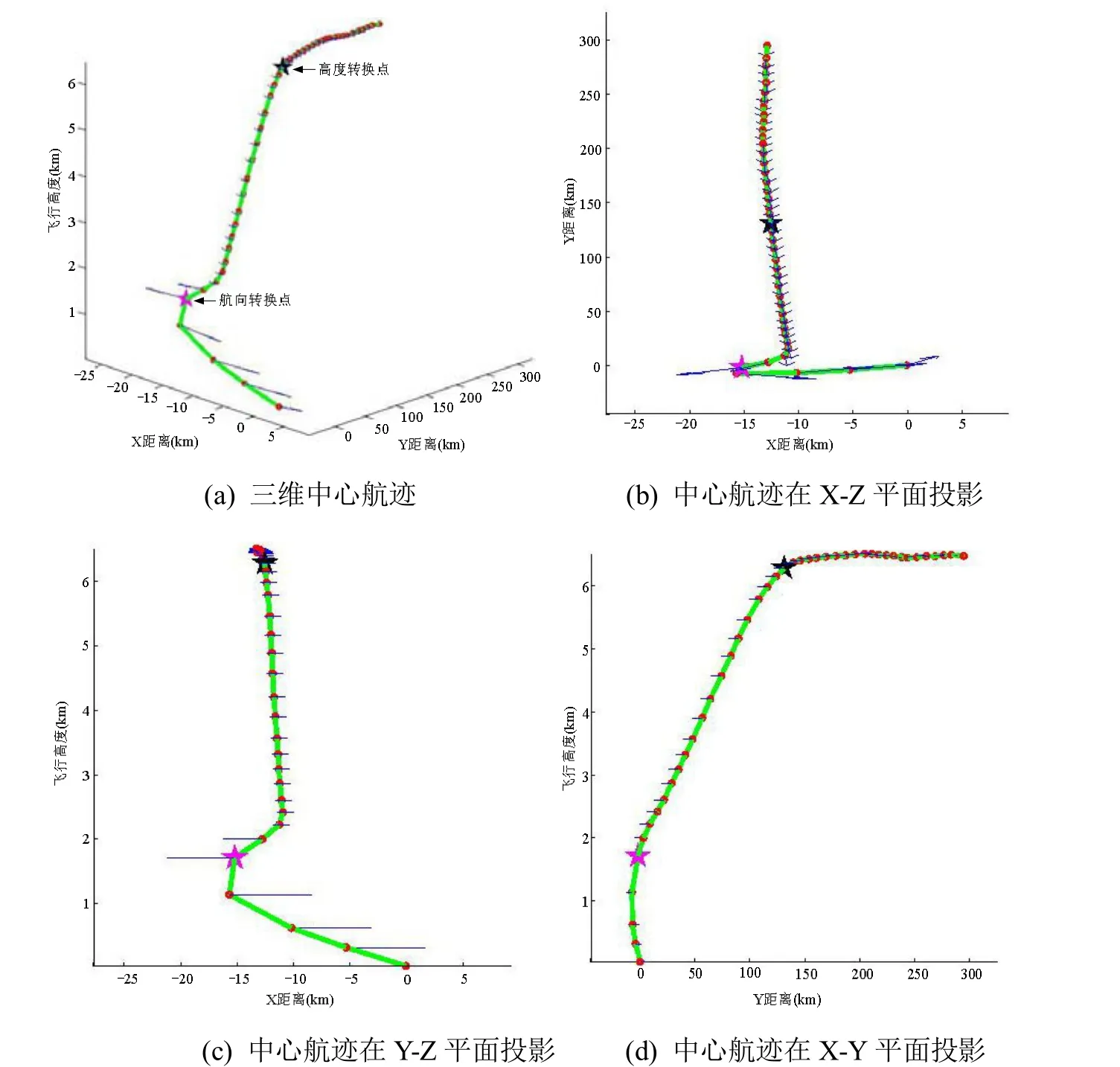
图10 中心航迹的特征点识别

3 结 论

本文基于计算几何中骨架提取的方法，提出了一种针对终端区航迹簇的中心航迹提取方法。在将雷达航迹数据转化为三维点云模型之后，采用沿飞行方向的自适应采样方法对原始点云进行采样，得到代表点集。充分利用代表点的航向信息建立图结构，并通过退化算子进行优化，形成初始中心航迹曲线。最后先后通过均匀化处理以及光滑处理，生成最终的中心航迹曲线。在此基础上，通过平均航向和平均速度的计算，识别中心航迹的特征点。通过对真实航迹簇数据进行实验，验证了本文方法的正确性、有效性和鲁棒性。本文方法在航迹聚类与分析、4D航迹规划与预测等领域具有重要的意义和价值。为了更好地分析终端区内不同航班之间的相互影响，降低发生飞行冲突的可能性，下一步工作将重点围绕针对多航迹簇的中心航迹提取问题展开研究。

[1] 腾 鹏,黄 俊,张 斌. 三维航迹的 B 样条曲线拟合算法[J]. 火力与指挥控制,2007,32(9): 115-118.

[2] 彭建亮,朱 凡,孙秀霞,孙 彪. 基于离散PSO和Voronoi图的无人机航迹规划方法研究[C]//第二十六届中国控制会议论文集,湖南: 2007: 804-807.

[3] 李新胜,兰时勇,李 纲,肖 朝. 利用 BéZier和 B样条曲线模拟飞机航迹的方法[J]. 西南交通大学学报,2011,46(6): 1040-1045.

[4] Gariel M,Srivastava A N,Feron E. Trajectory clustering and an application to airspace monitoring [J].IEEE Transactions on Intelligent Transportation Systems,2011,12(4): 1511-1524.

[5] 王增福,潘 泉,郎 林,程咏梅. 基于减法聚类的动态航迹聚类算法[J]. 系统仿真学报,2009,21(16):5240-5243.

[6] 赵恩来,郝文宁,赵 飞,陈 刚,邵校莎莎. 改进的基于密度的航迹聚类算法[J]. 计算机工程,2011,37(9): 270-272.

[7] Dey T K,Sun Jian. Defining and computing curve-skeletons with medial geodesic function [C]//Proceedings of the fourth Eurographics symposium on Geometry processing 2006. Aire-la-Ville,Switzerland:Eurographics Association,2006: 143-152.

[8] Au O K-C,Tai C L,Chu H K,Cohen-Or D,Lee T Y.Skeleton extraction by mesh contraction [J]. ACM Transactions on Graphics,2008,27(3): 1-10.

[9] Sundar H,Silver D,Gagvani N,Dickinson S. Skeleton based shape matching and retrieval [C]//Proceedings of the International Conference on Shape Modeling and Applications. Washington DC,USA: IEEE Computer Society,2003: 130-142.

[10] Cornea N D,Demirci M F,Silver D,Shokoufandeh A,Dickinson S J,Kantor P B. 3D object retrieval using many-to-many matching of curve skeletons [C]//Proceedings of the International Conference on Shape Modeling and Applications. Washington DC,USA:IEEE Computer Society,2005: 368-373.

[11] Cao Junjie,Tagliasacchi A,Olson M,Zhang Hao,Su Zhixun. Point cloud skeletons via laplacian-based contraction [C]//Proceedings of the International Conference on Shape Modeling and Applications.Washington DC,USA: IEEE Computer Society,2010:187-197.

[12] Lee I K. Curve reconstruction from unorganized points [J]. Computer Aided Geometric Design,1999,17(2): 161-177.

[13] Tagliasacchi A,Zhang Hao,Cohen Or D. Curve skeleton extraction from incomplete point cloud [J].ACM Transactions on Graphics,2009,28(3): 1-9.

[14] Zhao Yuandi,Cao Junjie,Su Zhixun,Li Zhiyang.Efficient reconstruction of non-simple curves [J].Journal of Zhejiang University-Science C,2011,12(7): 523-532.

[15] 王 超,郭九霞,沈志鹏. 基于基本飞行模型的4D航迹预测方法[J]. 西安交通大学学报,2009,44(2):296-300.