应用于灰度图像分割的基于流体静力学原理活动轮廓模型

黄文钧 ， 方丽菁

（1. 广西民族大学信息科学与工程学院，广西 南宁 530006；2. 广西民族大学理学院，广西 南宁 530006；3. 广西混杂计算与集成电路设计分析重点实验室，广西 南宁 530006）

图像分割是将一幅图像划分成若干个互不相交的区域，使得灰度、彩色、纹理等特征在同一个区域内表现出一致性或相似性。传统的图像分割方法有：阈值检测方法、拉普拉斯算子、Canny 算子、分水岭方法等；比较高级的方法有：均值移位方法、参数活动轮廓模型、几何活动轮廓模型等[1]。参数活动轮廓模型以“Snakes模型”为代表[2]，而几何活动轮廓模型以“水平集方法”为标志[3]。水平集方法采用一类三维曲面（水平集函数）的零水平集隐式地表示演化曲线，通过曲面的演化实现曲线拓扑变化。水平集方法可以应用于梯度图像或二值图像分割[3-6]，也可以应用于灰度图像分割[7-8]。将水平集方法应用于灰度图像分割的经典模型当属C-V模型[7]。对于目标灰度和背景灰度可以近似看成“二值”的图像，C-V模型可以快速且精确地将目标分割出来；但对于灰度变化较复杂的图像，该模型就不能有效地实现目标轮廓分割了。针对C-V模型存在的这一问题，许多学者提出了解决问题的方法。蒋建国等[8]提出一种无须重新初始化的变分水平集自适应主动轮廓模型，该模型利用图像的局部特性自适应决定曲线的演化，同时加入局部C-V能量项，改进边界停止函数，提高对灰度分布重叠、分布不均匀及弱边界处理的鲁棒性，并加快曲线演化的收敛速度。李秀等[9]提出一种基于局部区域信息的活动轮廓模型，该模型引入二值核函数提取图像局部信息，结合GAC和C-V模型的优点对弱边界和模糊边界能够产生较好的分割效果。林颖等[10]针对医学图像中存在的灰度不均匀现象，提出一种变分水平集分割模型，将邻域信息引入到基于Bayes决策准则的水平集分割框架中,以增强灰度不均匀条件下弱目标边界的识别能力。任继军和何明一[11]提出整合图像的灰度分布信息、邻域空间信息以及图像所具有的模糊信息构造三维向量（灰度值，模糊均值，模糊中值），提出基于三维直方图的改进C-V水平集图像分割方法。对于灰度图像分割问题，人们除了研究水平集活动轮廓方法之外，还研究其他方法。文献[12]提出一维最小误差阈值法的二维推广，应用于灰度图像分割；文献[13]研究灰度分级的图像分割算法；文献[14]研究灰度特征聚类的图像自动分割方法；文献[15]研究基于模糊集的灰度图像阈值分割算法；文献[16]针对图像阈值分割问题，根据遗传算法理论提出最优进化图像阈值分割算法。本文将研究新的活动轮廓图像分割方法，提出一种新的活动轮廓模型：“基于流体静力学原理的活动轮廓灰度图像分割模型”。我们将从一个基于流体静力学原理的物理模型入手，再导出对应的数学模型。

1 流体静力学基本知识

为了方便下面的讨论，先将流体静力学的基本知识[17]作一简单介绍：

（1）流体处于静止状态时，作用在流体表面上的力只有压力。

（2）流体静压力的两个特性：流体静压力的方向必沿作用面的内法线方向；流体中任意一点所受的各方向压力相等。

（3）欧拉(流体)平衡微分方程式

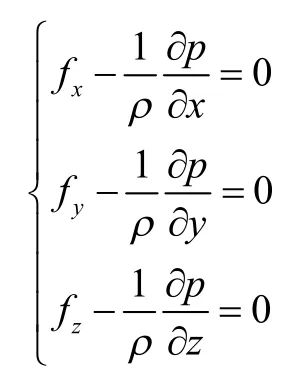
其中符号

分别表示质量力在x轴、y轴、z轴上的投影，其中：

分别表示流体静压力在x轴、y轴、z轴方向单位距离上压强的变化率；符号ρ表示流体密度。

该方程式表明流体处于平衡状态时，单位质量流体所受的表面力与质量力彼此相等。

（4）静止流体中凡压强相等的各点联结起来组成的平面或者曲面称为等压面。

2 一个基于流体静力学原理的物理模型

（1）将一组刚体装入一个具有优良弹性的薄橡皮口袋中，将该口袋密封。

（2）将这个已密封的口袋，连同里面的刚体一起，浸没入一个具有足够深度的湖中，在水压力足够大的位置悬停。这时该口袋，连同其中的刚体，处于平衡状态。

（3）通过此口袋以及其中的所有刚体，作一个理想的等压剖面。在这个理想的等压剖面上，含有该口袋的一个确定剖面（是一条封闭的平面曲线），也含有每一个刚体的一个确定剖面（每一个剖面均为一个平面区域）。

（4）缓慢地抽出这个口袋里的空气，这时该口袋上各点在其内法线方向上承受的合力逐渐增大，平衡状态被打破，该口袋上各点沿着自己的内法线方向从外向里缓慢移动，逼近内部的刚体；这个过程反映到该等压剖面上，出现一个相应现象：口袋剖面上的任意一点，在其内法线方向上承受的合力越来越大，迫使该点沿着自己的内法线方向从外向里缓慢移动,带动曲线从四周向里缓慢收缩，逼近内部的刚体剖面。

（5）随着口袋里的空气逐渐稀少，在流体压力以及橡皮弹力的作用下，此口袋从各个方向向内部的刚体缓慢逼近，逐渐将各个刚体隔离；和上面叙述的情形相似，反映到该等压剖面上，也出现一个相应现象：口袋剖面从四周向内部的刚体剖面缓慢逼近，逐渐将各个刚体剖面隔离。

（6）当口袋里形成真空时，在水压力以及橡皮弹力的作用下，口袋的内表面将粘在刚体的表面上，或者内表面相互粘贴在一起，口袋里将没有任何缝隙。由于物品是刚体，不可压缩，根据欧拉平衡方程式，口袋将处于新的平衡。相应地，等压剖面上的口袋剖面，一条闭合曲线，其内部也没有任何缝隙，曲线粘在刚体剖面的轮廓上，或者内侧粘贴在一起。此时，在该等压剖面上，剪掉那些联结在两个刚体剖面之间的曲线段，即得到各个刚体剖面的分割。

3 模拟上述物理模型的数学模型

以下所有变量均在正整数集里取值：

i,j,m,n,s,t,x,y,Δs,Δt∈N∪{0}

（1）设一幅灰度图像为：

其中，1≤i≤m,1≤j≤n,[m,n]=size(I),m,n≥1。

（2）在平面上定义一条简单闭合连续曲线：

C(s,t) = {(x(s,t),y(s,t)) | s≥0,表示弧长}

其中，t(t≥0)表示时刻，(x(s,t),y(s,t))表示曲线上的点。

（3）在曲线C(s,t)上定义一个函数并将其初始化：

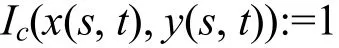
以模拟物理模型中的口袋剖面各点初始所受的流体静压力。

（4）将曲线C(s,0)包围灰度图像 I 的目标，模拟口袋剖面包围刚体剖面。

（5）定义如下偏微分方程为驱动曲线C(s,t)的数学模型：

（u＞0; u是本模型最重要的阈值，须合理定义和调整，方有可能得到优质的图像分割）

（6）应用微分方程（*）驱动曲线C(s,t)。

将微分方程(*)应用于闭合曲线C(s,ti-1)上任意一点(x(sj,ti-1),y(sj,ti-1))，可产生曲线C(s,ti)的相应一个点：

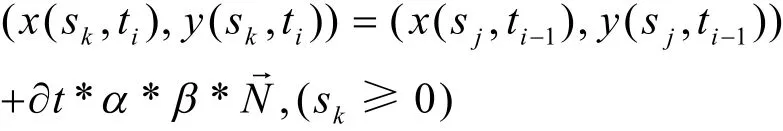
其中，ti-ti-1=Δt，Δt=1，∂t=1。

将此点 (x(sk,ti),y( sk,ti))添加到曲线C(s,ti)的相应位置，并且记录此点对应的“α*β”：

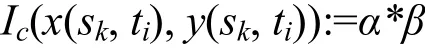
（7）如果曲线C(s,ti)上任意相邻两点

(x(sk,ti),y(sk,ti))和(x(sk-1,ti),y(sk-1,ti))满足下面不等式：

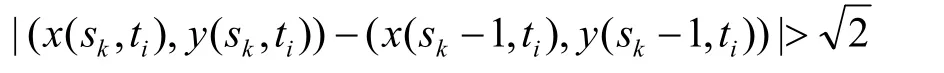
则用曲线

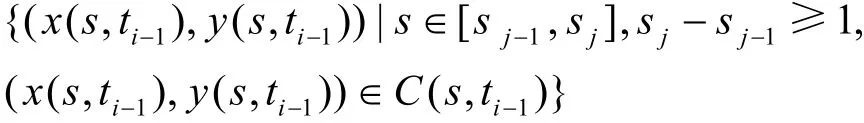
连接并加入到曲线C(s,ti)之中，其中

函数Ic(x,y)在这段连接曲线上的取值保持不变。

（8）如果闭合曲线C(s,ti)除了端点之外，还有另外重合点，则将曲线C(s,ti)裁剪成几条简单闭合曲线，从中选取那些周长大于预定阈值CL(＞0)的简单闭合曲线，连同在它们上面定义的函数Ic(x,y)，一起存储于集合W中。如果集合W非空，从集合W中取出其中一条曲线，仍记为C(s,ti)。

（9）计算下面表达式：

若最小值min随t值增大而未趋于稳定，则跳转第(6)步继续演化曲线C(s,t)。

如果最小值min为零或者随t值增大而趋于稳定,暂停对曲线C(s,t)的演化，并进行如下处理：

如果曲线C(s,t)（对应最小值min的曲线）的周长|C(s,t)|足够长,即|C(s,t)|≥CL，则曲线C(s,t)可看成目标轮廓并加以保存，同时初始化函数：

Ic(x(s,t),y(s,t)):=1

并跳转第(6)步继续驱动该曲线C(s,t)，搜索嵌套的目标。如果曲线C(s,t)的周长|C(s,t)|过短，即|C(s,t)|＜CL，则被此曲线包围的目标不予考虑，当噪音处理，放弃此曲线。

（10）如果集合W不空，从中取出一条曲线并记为C(s,ti-1)，跳转第(6)步继续执行。

（11）结束。

4 模型分析

4.1 物理模型分析

物理模型中的“等压剖面”实际上是一个水平面，在该水平面上，仅考虑呈水平方向的流体压力。对于口袋剖面，一条闭合的橡皮曲线,如果不考虑质量力，曲线上任意一点未接触刚体剖面边缘之前，所受的力只有两个：一个是朝内法线方向的静水压力，另一个是朝外法线方向的气体压力。

流体静力学原理告诉我们，同在一个水平面上的点，所受的压强相等；从而在等压面上的封闭曲线，上面的点所受的压力也相等。

在抽出该口袋里的空气之前，该曲线上任意一点都处于平衡状态，此时根据欧拉方程可以推知：曲线上任意一点在法线方向上合力为零。在“缓慢地”抽出空气过程中，静水压力不变，而气体压力变小，曲线上的点在法线方向上所受合力不为零，原来的平衡状态被改变，曲线上的点发生位移。由于抽出空气过程“缓慢”，流体状态依然可以看成“静态”，曲线上任意一点所受的静水压力和气体压力依然朝着法线方向。随着气体压力缓慢变小，曲线上任意一点在静水压力和气体压力的合力作用下朝内法线方向缓慢移动，带动着整条曲线缓慢地演变。曲线上任意一点的法线方向由该点和其邻域共同确定，曲线的演变带动着各点法线方向的改变，而各点法线方向的改变又导致曲线形状的变化，所以该曲线在流体静压力的作用下可以演变各种几何形状，可以表现形状复杂的目标轮廓。

曲线的任意一点，如果在自己的内法线方向上没有障碍物，则受力大小相等，在同一个时间间隔内移动的距离也相等。

由于物品是刚体，不可压缩，边缘不可移动。曲线上的点沿内法线方向移动时若碰上刚体边缘，受边缘惯性力和流体压力在法线方向上的合力（合力为零；该点所受气体压力为零）作用，该点停止移动，根据欧拉平衡方程，该点在曲线后续演变的过程中保持平衡。

由于曲线是橡皮带，有良好的弹性，在演变过程中曲线无重合点，也不断裂。

4.2 数学模型分析

本数学模型是上述物理模型的模拟，其中的灰度图像I(i,j)对应物理模型的“口袋内部剖面”；灰度图像I(i,j)的目标对应“刚体剖面”；曲线C(s,t)对应“口袋剖面”。

偏微分方→程 (*) 驱动曲线C(s,t)上的点沿着内法线方向N缓慢移动，模拟口袋剖面在静流体压力作用下缓慢收缩过程。

偏微分方程(*)的参数β来自函数Ic(x(s,t),y(s,t))，表征曲线上的点是否已接触目标边缘：β=0表征曲线C(s,t)上的点(x(s,t),y(s,t))已接触目标边缘，不再移动；以此方法模拟口袋剖面上的点，接触刚体边界后的平衡状态；β=1表明曲线C(s,t)上的点(x(s,t),y(s,t))目前（时刻t）是否接触目标边界尚未确定，需要在时刻 t+Δt 通过偏微分方程(*)加以考察：如果参数α=0，表明该点(x(s,t),y(s,t))已接触目标边界；如果α=1，表明该点还未接触目标边界。因此β*α=1表征曲线C(s,t)上的点(x(s,t),y(s,t))未接触目标边界，可以沿内法线方向继续移动；以此方法模拟口袋剖面上的点，未接触刚体边界之前仍沿流体静压力方向移动。

在物理模型中，口袋剖面是一条闭合的橡皮细线，具有良好的弹性，在水压力和口袋里气体压力的作用下不会产生重合点。基于以上认识，本数学模型采用简单闭合连续曲线模拟口袋剖面。

本数学模型处理曲线重合点问题的方法是：在重合点处将曲线剪断，将曲线分成若干条简单闭合曲线；而处理曲线间断问题的方法是：用直线或曲线连接间断处，以此方法模拟橡皮线的可延展性能。

在本数学模型里，灰度图像的目标是一个平面区域，有一定的面积，也有一定的周长。因此，我们预先给目标定义一个判别标准， 预设一个正整数阈值。在闭合曲线演化的过程中，若发现曲线周长小于该阈值，就可以认为该闭合曲线内部无目标，可放弃该曲线。曲线的长度以点（像素）的数目表征。

当曲线上某个像素的内法线方向和直线y=x或y=-x平行时，沿此像素内法线方向的最邻近像素，和该像素的距离等于2，大于一个像素距离，这时此像素要选取向内水平方向或竖直方向为移动方向，以保证

5 实验对比

本实验将本文模型、C-V模型、李纯明模型（一种水平集模型）以及标记分水岭方法[18]应用到5幅图像上，并作了对比，相关数据已在表1中列出，实验结果见图1～6。

表1 本文模型、C-V模型、李纯明模型以及分水岭方法的实验数据

本文模型、C-V模型、李纯明模型以及标记分水岭模型，分割的时间平均值依次为：45.2153、24.5545、64.7498、0.4742。本文模型的速度比C-V模型慢，原因是本文模型每次迭代至多让曲线的点移动一个像素，收敛速度较慢。

对于背景和目标灰度可以近似分为二值的图像（图3(c1)），四种模型都可以将目标分割出来，但李纯明方法对凹尖角仍然难以分割，就是增加迭代次数也是收效甚微（图5(d1)）。和李纯明方法相比，本文模型对凹尖角的分割效果有所改善，但不如C-V模型和标记分水岭方法。

对于背景和目标灰度比较复杂的图像（图1(b)），C-V模型和李纯明方法对目标的轮廓分割不完整（图4(a2,b3)和图5(a1,c1,e1)）；而标记分水岭方法对目标轮廓分割基本完整，但过分割现象较严重（图6(a1)）；本文模型对目标轮廓分割基本完整（图1和图3），并且能够有效地控制过分割现象（数学模型中的参数β起的作用）。

C-V模型对初始曲线位置比较敏感，位置不同，分割的区域也不同（图2(b3,c3)）；本文模型对初始曲线的形状以及位置无特殊要求，仅要求初始曲线是简单曲线并且包围待分割的目标。

对于边界比较模糊的目标（图 4(b1)），C-V模型、李纯明模型以及标记分水岭方法等，分割的轮廓有“越界”现象，曲线都被演化进了目标内部，丢失了部分轮廓（图4(b2)、图5(c1)和图6(c1)）；本文模型能够比较好地控制“越界”现象（数学模型中的参数 β起的作用），能够比较正确地分割目标的模糊轮廓（见数学模型第(5)步关于阈值u的说明，如图3(b2)）。

本文模型能够分割多目标，见数学模型第(8)步和图1(e)；也能够分割内嵌目标，见数学模型第(9)步和图3(d2)。

本文模型要求初始曲线一定要包围目标，如果曲线的某一段置在目标内部，那就有可能因为灰度变化平缓而丢失一部分目标的轮廓。如图3(a1)，初始曲线有一段在目标内部（绿色区域），本文模型没能分割出绿色区域的轮廓。

本实验所用的电脑参数为：Intel(R)Xeon(R)CPU E31230@3.20GHz；内存2 G。用MATLAB语言编程，用其中的函数 cputime()计时。

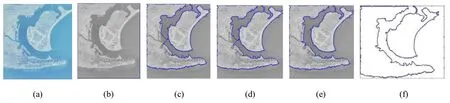
图1 本文模型的分割过程：(a)原图; (b)显示初始曲线的位置; (c)演化曲线即将出现重合点; (d)原演化曲线即将被分成两条简单曲线; (e)两条简单曲线独立演化的结果; (f)提取轮廓线。迭代400次，耗时87.2046

图2 C-V模型初始曲线位置对分割结果的影响: (a)原始图片; (b1～b3)和(c1～c3)两组图片分别为演化曲线在两个不同的初始位置上对应的两种分割结果; (b2)图需迭代50次，耗时0.4212; (c2)图需迭代60次，耗时0.3276

图3 本文模型实验结果: (a3)图需迭代40次，耗时0.7020; (b2)图需迭代160次，耗时8.4085; (c2)图需迭代90次，耗时0.3744; (d2)图需迭代800次，耗时129.3872

图4 C-V模型实验结果: (a2)图需迭代2000次，耗时111.1975; (b2)图需迭代200次，耗时5.3976; (c2)图需迭代20次，耗时0.2184; (d2)图需迭代30次，耗时5.5380

图5 水平集方法（李纯明模型）实验结果: (a1)图需迭代900次，耗时44.1795; (b1)图需迭代760次，耗时6.2712;(c1)图需迭代590次，耗时12.7609; (d1)图需迭代600次，耗时6.6144; (e1)图需迭代1100次，耗时253.9228

图6 标记分水岭方法实验结果: (a1)图耗时0.7644; (b1)图耗时0.1872; (c1)图耗时0.4212;(d1)图耗时0.2652; (e1)图耗时0.7332

6 结 论

本文模型能够分割背景灰度和目标灰度近似于二值的图像，也能够分割背景和目标灰度都比较复杂的图像，分割的目标轮廓线基本完整。本文模型还可以有效地控制过分割现象。对于灰度复杂的图像，分割时间较长，今后将研究提速问题。

[1] Milan Sonka,Vaclav Hlavac,Roger Boyle著,艾海舟,苏延超译. 图像处理、分析与机器视觉[M]. 3版. 北京: 清华大学出版社,2011: 124-224.

[2] Kass M,Witkin M,Terzopoulos D. Snakes：active contour models [J]. International Journal of Computer Vision,1988,1(4): 321-331.

[3] Li Chunming,Xu Chenyang,Gui Changfeng,Fox M D. Level set evolution without re-initialization: a new variational formulation [C]//Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR'05),2005:430-436.

[4] 张万涛,李维国. 利用曲率信息的图像分割改进模型[J]. 中国图象图形学报,2011,16(8): 1385-1392.

[5] 冷大玮,马洪兵,张爱武,孙卫东. 曲率无关方向扩散及改进型 Chan-Vese主动轮廓模型[J]. 计算机辅助设计与图形学学报,2012,24(2): 161-169.

[6] 周亚男,程 熙,骆剑承,沈占锋,胡晓东. 改进GVF的自动 Snakes模型[J]. 中国图象图形学报，2012,17(2): 256-262.

[7] Chan T F,Vese L A. Active contours without edges [J].IEEE Transactions on Image Processing,2011,10(2):266-277.

[8] 蒋建国,任 婧,郝世杰,詹 曙,李 鸿. 自适应主动轮廓模型下的骨关节MRI快速分割[J]. 中国图象图形学报,2011,16(7): 1199-1205.

[9] 李 秀,孙长银,杨万扣. 局部活动轮廓模型对灰度不均匀图像的分割[J]. 科技通报,2011,27(5):647-651.

[10] 林 颖,印桂生,杨 耘. 基于变分水平集的灰度不均匀医学图像分割[J]. 计算机工程,2010,36(24):203-205.

[11] 任继军,何明一. 一种基于三维直方图的改进 C-V模型水平集图像分割方法[J]. 红外与毫米波学报,2008,27(1): 72-76.

[12] 范九伦,雷 博. 灰度图像最小误差阈值分割法的二维推广[J]. 自动化学报,2009,35(4): 386-393.

[13] 罗明俊,万幼川,秦 昆. 基于灰度分级的图像分割算法的研究[J]. 地理空间信息,2005,3(6): 9-10.

[14] 惠 飞,黄士坦. 基于灰度特征聚类的图像自动分割方法[J]. 武汉大学学报(工学版),2009,42(3):405-408.

[15] 陆 懿,陈光梦,陈 松. 一种基于模糊集的灰度图像阈值分割算法[J]. 2007,43(20): 75-77.

[16] 林正春,王知衍,张艳青. 最优进化图像阈值分割算法[J]. 计算机辅助设计与图形学学报,2010,22(7): 1201-1206.

[17] 郭仁东,吴慧芳,李 刚. 水力学[M]. 2版. 北京:人民交通出版社,2012: 21-39.

[18] 高 丽,杨树元,李海强.一种基于标记的分水岭图像分割新算法[J]. 中国图象图形学报,2007,12(6): 1025-1032.