捞油抽子密封橡胶筒力学性能研究

崔健，谢劲松

（长春理工大学 机电工程学院，长春 130022）

0 引 言

随着石油资源的消耗，地下油层的含油量也在逐渐降低，这导致部分油井产油率下降，传统的抽油方式已不适合在此类产油低的井上工作。因此，在最近十年中一种新型采油方式得到发展，柔性捞油抽子替代了刚性抽油杆和泵的组合方式，与传统抽油方式相比，它克服了小冲程、多冲次的缺点，可以实现长冲程，同时降低了冲程次数。其中密封橡胶筒这一零件至关重要，通过捞油抽子在井下的往复运动，液柱自身重力使密封橡胶筒膨胀或复原，以实现提捞油的功能。但是在这一工作过程中存在一个矛盾问题，密封橡胶筒在与管壁接触时必定会与管壁产生摩擦，因为密封橡胶筒变形过大会导致磨损程度发生变化，过度磨损会加剧抽子损坏，直接加大了抽油漏失率。因此，需要找到在密封橡胶筒形变、应力、与摩擦力、磨损之间的关系。

1 密封橡胶筒几何模型建立

依据捞油抽子工作原理和加工工艺要求建立密封橡胶筒模型，如图1 所示。

图1 密封橡胶筒

2 密封橡胶筒形变、应力、摩擦力、磨损之间关系建模

密封橡胶筒的形变、应力与材料力学、弹性力学相关，摩擦力随着井下位置变动而变化，在其它因素不变的情况下，磨损与摩擦力成线性关系。

2.1 理论模型基本假定

1）假定橡胶密封筒工作范围在弹性变形范围内，并且不会达到塑性变形。2）在满足工作要求下对密封橡胶筒实物进行简化处理，例如去掉倒角、螺纹等。3）刚性油管相对于弹性密封橡胶筒接触过程中产生的形变忽略不计。4）假定橡胶密封筒是均匀的、具有各向同性［1］。5）密封橡胶筒轴向、径向上受均布载荷。

2.2 数学模型的建立

如图2 所示，由于密封橡胶筒是回转体，在井下其受力状况相对于轴线对称，且轴向受力和径向受力情况都为均布载荷，所以对于轴对称受力问题设在极坐标下考虑［2］。

另外，由于密封橡胶筒变形后与油管内壁完全接触，在井下特定位置下它将不变形，轴向上不会产生伸缩，但同时受到液柱重力影响，内部会产生轴向应力。因此将其简化为平面应变问题。即橡胶筒内半径为a，与油管内壁接触时外半径为b，受内压qa，油管内壁给的外压qb。

1）推导所需主要符号：直角坐标x，y，z；极坐标ρ，φ；体力分量fp，fφ（极坐标系）；应力分量正应力σ，切应力τ；应变分量线应变ε，切应变γ；应力函数Φ，密度ρ液，重力加速度g 橡胶筒距离井口位移h；弹性模量E，切变模量G，泊松比μ，动摩擦因数f；几何尺寸橡胶筒内半径a，橡胶筒与油管内壁的外半径b，接触厚度c。量纲采用国际单位制（SI）。

2）依据上述假设，由弹性力学公式得极坐标中的平衡微分方程［2-3］：

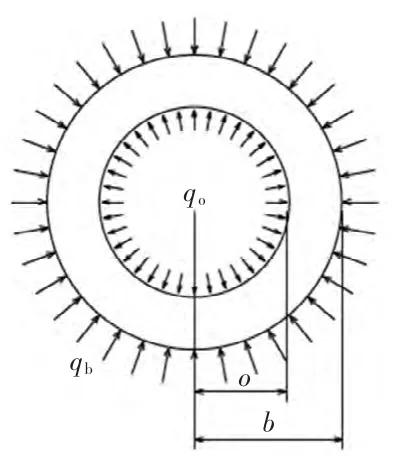
图2 橡胶筒受力分布

根据实际情况密封橡胶筒的径向、周向不受外力，故fρ=0，fφ＝0。

3）由弹性力学知，极坐标中的几何方程

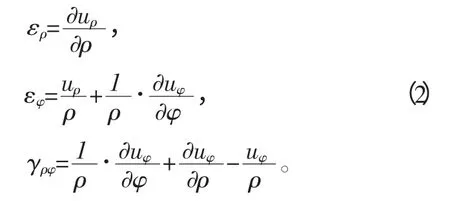
4）由弹性力学得极坐标中的平面应变物理方程：

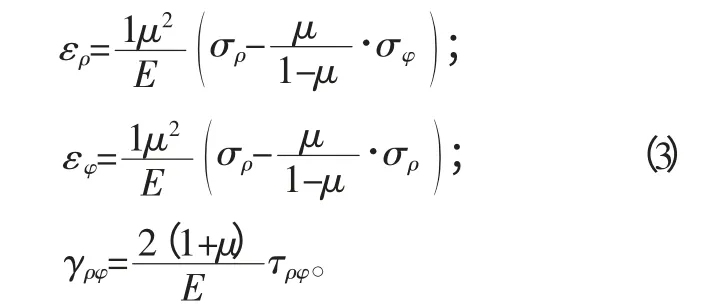
5）由弹性力学得，应力函数Φ 可以表达极坐标中的应力分量如下式。

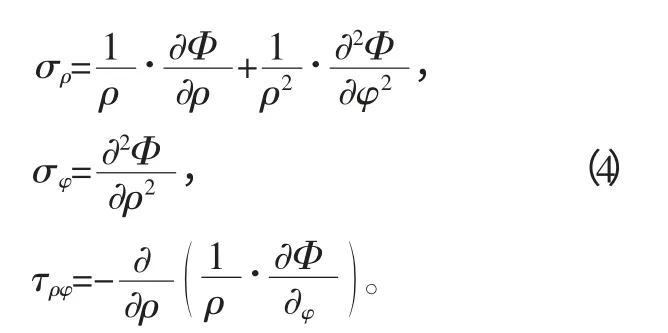
6）极坐标中的相容方程

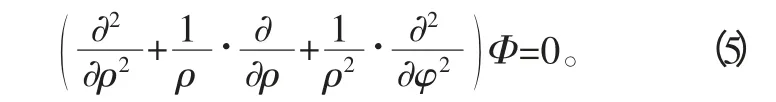
由于密封橡胶筒是轴对称应力，所以用弹性力学中逆解法求解应力函数，应力函数Φ 只是径向坐标ρ 的函数，即：Φ＝Φ（ρ）。

在这样情况下，式（4）简化为：

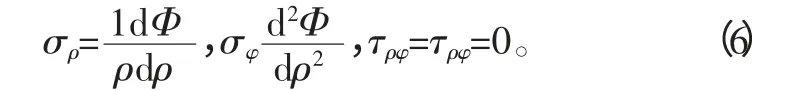
将式（6）带入到（5）得出：

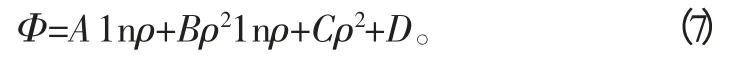
（7）式中A、B、C、D 为任意常数。将式（7）带入到式（6）中得应力分量：

由式（8）知，求出任意常数A、B、C 则应力分量表达式确定。

7）根据边界条件要求：

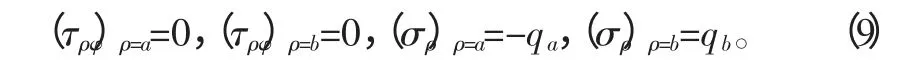
带入式（8）整理后得拉梅方程

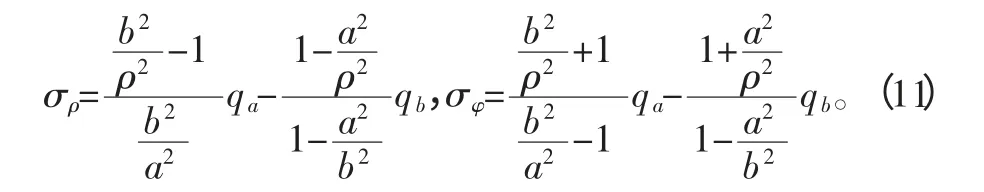
8）由弹性力学应力坐标变换公式：

得出公式： σxσy=σρσφ（12）

得 σz＝μ（σx+σy）。 （13）

将式（11）带入式（13）中得：

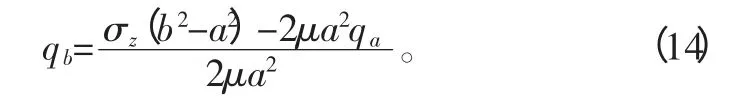
由于密封橡胶筒端部受均布载荷（液柱重力作用橡胶筒端面），其端面主矢不等于0、主矩等于0 符合静力等效原则，根据圣维南原理得出边界条件：

根据物理学知识，物体在同一位置上受到液体产生的压强大小相等，再根据基本假定5 得：

将式（15）和（16）带入到式（14）中整理得：

2.3 物理模型建立

根据动摩擦力［4］公式F=f·FN。 （18）

密封橡胶筒在工作过程中，油管壁与筒壁产生相互的作用力，又因为弹性力学知边界条件下应力与面力大小相等。因此 EN＝qb·S，S=π·b·c。 （19）

最后将式（19）与（17）带入式（18）中，整理得：

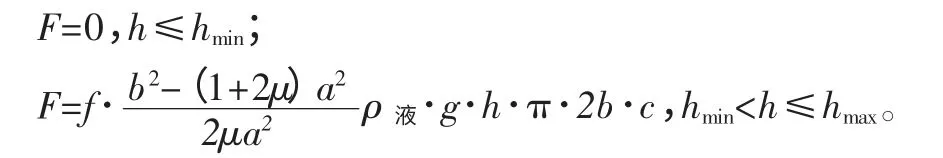
即：F=0，0＜h≤hmin；F=K·h，hmin＜h≤hmax。 （20）其中系数K 作为几何参数a 和泊松比μ 之间的函数。hmin由材料力学限定，hmax由塑性力学限定。

3 试验结果分析

试验结果与理论计算结果存在误差，出现误差的原因是随机因素引起。但误差在可控范围内，符合工程实际需求。试验结果如表1、图3、图4 所示。

4 结 语

推导出的结论分如下几部分表述，1）几何参数包括a、b、c，根据工程需要a 可以为变量，其它为常量；2）材料特性，橡胶筒泊松比μ 可以通过改变材料配方来改变其值，可以认为是变量。因此对于密封橡胶筒对油管内壁摩擦力问题通过几何尺寸、材料性质对其进行定量分析。

表1 参数表

图3 摩擦力与井下位移关系

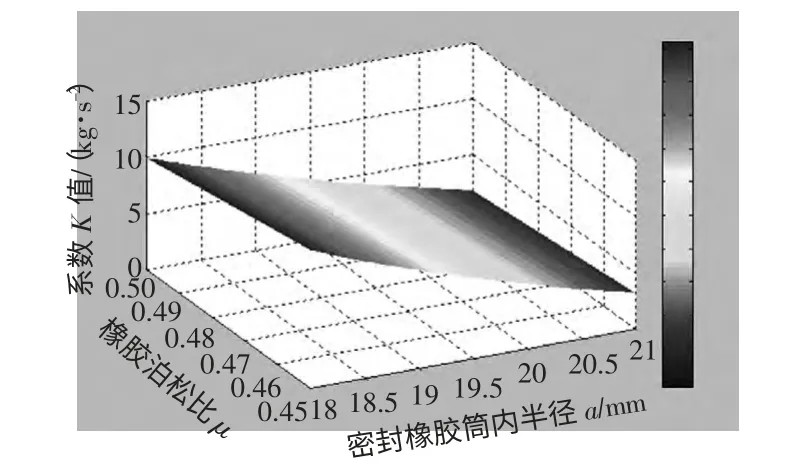
图4 系数K 与橡胶筒内半径、泊松比关系

［1］ S.P.铁木辛柯，J.N.古地尔.弹性理论［M］.北京：高等教育出版社，2013：75-88.

［2］ 徐芝纶.弹性力学［M］.北京：高等教育出版社，2006.

［3］ 谷超豪，李大潜，陈怒行.数学物理方程［M］.2 版.北京：高等教育出版社，2002：68-91.

［4］ 哈尔滨工业大学理论力学教研室.理论力学［M］.北京：高等教育出版社，2009：112-114.