基于THERP—Markov原理的高铁列调人因可靠性分析

徐培娟，彭其渊，文 超，郭经纬，占曙光

（西南交通大学 交通运输与物流学院，成都，610031）

基于THERP—Markov原理的高铁列调人因可靠性分析

徐培娟，彭其渊，文 超*，郭经纬，占曙光

（西南交通大学 交通运输与物流学院，成都，610031）

在高速铁路调度指挥系统中，列调人员通过调度终端来指挥铁路现场的生产活动，调度员的操作直接影响列车的运行.本文引入核电工业中的THERP理论，结合列调操作特征来计算静态条件下列调操作失误率及其置信区间；并结合马尔科夫链原理，建立状态转移率方程，通过拉普拉斯变换得出单影响因子作用下列调可靠性的状态概率变化规律.最后，以执行列控限速任务为例，得出列调的静态失误率及压力影响因子作用下人因动态可靠性变化规律.研究结果表明：在压力适中的情况下，列控限速执行失败率最低，为0.010 4.

铁路运输；人因可靠性；THERP理论；马尔科夫链；动态可靠性

1 引 言

人因可靠性分析是研究人的认知、判断及操作行为对生产活动安全及可靠性的一种分析方法.对于高速铁路调度指挥系统而言，列车调度人员（简称“列调”）的操作直接影响高速列车的行车安全，因此，利用人因可靠性理论研究列调人员操作可靠性的问题具有十分重要意义.

人因可靠性理论与研究方法主要分为三类：一类是利用结构化建模和数学计算方式，如人误率预测技术（TEHRP）[1,2]、人的认知可靠性模型（HCR）[3,4]、成功似然指数法（SLIM）[5]等；第二类从认知方面着手，通过分析环境、生理和设备状态等人为差错诱因，描述人因失误产生机理，如人误分析技术(ATHEANA)[6]、认知可靠性与失误分析法(CREAM)[7]和操作人员工作安全绩效评估法(MERMOS)；第三类是通过人工智能，仿真模拟技术[8]，研究具体领域的人因失误概率及诱因.

目前，我国针对高铁列调操作可靠性的研究尚处于起步阶段，缺少完整的理论体系和人员操作数据库.针对轨道交通中列调人员可靠性研究主要有：①专家经验法，分析行调人员的素质、业务水平等因素，对其提出不足及改进措施[9]；②系统分析法，依据专家评价法、层次分析法等方法，提出地铁调度人误模式[10]的结构化分析方法；③安全可靠性法，基于硬件故障模式、影响及危害分析（FMECA）技术，构建相应指标，分析突发事件下的行调人员的任务可靠性[11]，确定人误风险的等级的划分标准等.因受铁路系统数据库完备程度限制，而TEHERP理论具有方法论结构严谨、数据库相对完备等特点，本文拟采用TEHERP理论，研究列调人因可靠性问题，可为高速铁路调度指挥可靠性提供理论指导.

2 基于THERP理论的列调人因失误率静态分析

2.1 列调可靠性定义及理论概述

针对研究对象特点，列调人因可靠性R(t)定义为：在高速铁路行车指挥过程中，列车调度员在规定的时间t内，在规范条例m的要求下，无差错地完成列车运行状态监控、调度命令下达、列控限速设置、运行计划调整等规定任务(i,i∈I)且能合理有效地使用铁路资源的能力.概念公式为

式中 Ri（t）——任务i在规定的时间t内和规范要求m下执行的成功率，若任务i无需执行，则Ri(t)=1；

mi——任务i的规范条例，若mi=1，表示按规范执行，若mi=0，表示未按规范执行；

I——表示列调执行所有任务的集合；

η——合理使用人员或使用设备的概率.

对于静态列调人因失误分析，采用人因错误率预测技术（THERP），即通过建立人因可靠性分析事件树来分析任务执行过程中可能出现的与人有关的差错，进而分析标定人因失误概率，然后通过影响因子对标定人因失误概率进行调整，以获得基本的人为失误概率.最后利用其他任务或者事件影响该差错事件的逻辑关系,对失误率进行修正以获得最终的人为差错概率[12,13].

2.2 列调可靠性的THERP理论

高速铁路行车指挥岗位由列调与助调两人（在繁忙区段可能设2个助调，此时行车指挥人员为3人）组成，助调在列调的领导下辅助列调共同完成调度任务.文中研究列调为“广义列调”，即列调和助调均视为列调.为方便描述列调执行动作的层次性，将一项任务划分为若干个一级子任务，称为“一级动作单元”，而将其包涵的动作序列集称为“二级动作单元”.二级动作指由二人确认制度、人机校核等相关反馈子任务所包涵的动作，因此，每一个一级动作单元内的二级动作单元是反馈校验的并联元素.

（1）情景失误率.

一项调度任务由n（n＞0)个一级动作单元组成，只有当动作i(i=1,2,...,n)执行成功，动作i+1才会被执行；每个一级动作i由 j（j=1,2,3...mi)个二级动作单元组成，一级动作i失败导致的失误情景为Fi，计算方法为

式中 Pr(Fi)——失误情景Fi发生概率；

Pr(Fij)——一级动作单元i中第 j个动作失败概率.

由一级动作单元性质知，每个失误情景事件Fi是互斥的，则整个任务操作失败的总概率为

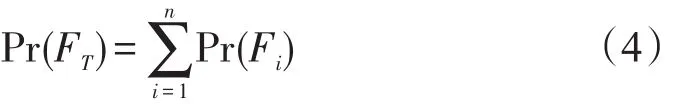
（2）情景失误率置信区间.

列调人员在标准状态下没有按规定操作或完成某一个动作的概率为标定失误概率Pr0(Fij)（即中值Mij，见人因失误手册[1]）.人因操作失误的类型主要分遗漏型与执行型错误，具体详细分类此处不再赘述.每一个标定失误概率都服从对数正态分布，通过边界因子EF可得失误率的90%的置信区间(Lij,Uij)：

式中 Mij——Pr0(Fij)的“最佳”值，即中值；

Lij——Pr0(Fij)的5%的置信度边界值，即置信度的下边界；

Uij——Pr0(Fij)的95%的置信度边界值，即置信度的上边界.

（3）修订情景失误率.

设影响列调动作失误的影响因素有p种，列调动作失误的影响因子（PSF）主要包括外影响因子、内影响因子及压力因子.定义乘法模型，对标定的人因失误概率进行修订：

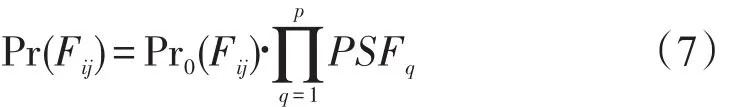
式中 PSF＞0,{0＜PSF≤1,称为正影响因子PSF＞1,称为负相关因子 .

由于0＜Prij(Fij)≤1，若根据式（7）计算出的Pr(Fij)＞1，修正为Pr(Fij)=1.

（4）动作关联性分析.

相继两个二级动作失误事件Fij和事件Fi(j+1)（或一级动作失误事件，Fi和Fi+1)之间相关程度定义为Pr(Fi(j+1)∕Fij)（或Pr(Fi+1∕Fi))，即事件Fij条件下事件Fi(j+1)的可能性，其共分为五级：完全相关(CD)，高相关(HD)，中相关(MD)，低相关(LD)，以及零相关(ZD).则Fi(j+1)发生的条件概率为

则根据条件概率公式，两个动作同时发生的概率为

式中 β为关联因子，根据关联度由高到低分别取值1，0.50，0.15，0.05和0[14].

（5）人因失误的置信区间.

任务执行失败的总概率Pr(FT)服从对数正态分布，那么，Pr(FT)中值及90%置信区间的上下边界值分别为

证明：

已知动作失误概率Pr(Fij)服从对数正态分布，根据对数正态分布的性质，事件Fi失误概率服从对数正态分布，因而对于lnPr(Fi)服从正态分布，其所对应的均值 μlnPr(Fi)和方差 μ2lnPr(Fi）为

而Pr(Fi)所服从对数正态分布的均值 μPr(Fi)和方差 μ2Pr(Fi）为

根据式(13)-式(16)，对于任务Pr(FT)服从近似对数正态分布(Metchell,1968)，因此下式成立：

因而对于lnPr(FT)服从正态分布，其所对应的均值 μlnPr(FT)和方差 μ2lnPr(FT）为

因此，将正态分布转换为对数正态分布，即可得Pr（FT)所服从对数正态分布的参数.

3 基于马尔科夫链理论人因失误率动态分析

THERP理论分析静态人因可靠性时不考虑时间对相关参数的影响，但在实际工作中，某些影响因子PSF是随时间变动的，因此本文拟引入马尔科夫链原理分析列调在变动影响因子作用下的动态可靠性变化规律[15,16]，做如下假设：

①列调人员的状态函数Vi(t)在时间t内是连续可导的；

②有且仅有一个影响因子是时间的因变量，其他影响因子是常量；

③变量影响因子的转移速率已知；

④各状态下人因失误率由THERP理论已求出.

假设可行性分析如下：

（1）对于假设条件1，若证明列调人员所处状态Vi(t)在时间t可导，即证明存在，具体证明如下：

系统处在各状态下的概率为连续时间变量{V(t),t≥0} ，具 体 表 示 为 {V0(t),V1(t),…,Vi(t),…, Vn(t)}，下标i表示系统所处的状态，i是系统状态集E中的元素，通常E={0 ,1,2,…,N}.对于∀i,j∈E,将p{V (t+Δt)=j|V(t)=i}记为在 t→t+Δt时间段内，系统由状态i转移到状态 j的概率，简记为pij，称为转移概率函数.

而系统中状态转移率是存在的，即可求Vi(t)的导数，所以假设条件1是成立的.

（2）目前在人机工程领域主要针对人的单影响因子（疲劳度、压力、噪声等）变化规律及转移率的分析.但多影响因子共同的作用规律及相关转移率的研究成果甚少，无法获取权威数据，为保证模型的严谨性，故作假设条件②、③.

（3）由于本文第2节已详细介绍了人因失误率的计算方法，故假设④可行.

通过以上假设分析，在时刻t，调度员操作结果的状态分布向量为 V(t)=(V0(t),V1(t),V2(t),…, Vn(t),F(t))，表示系统处于各个状态下的概率，其中Vi(t)表示调度员处于PSF第i种程度下操作成功的状态概率，F(t)表示作失败的状态概率（如图1）.

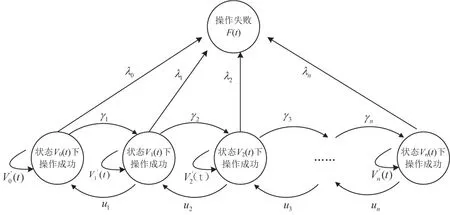
图1 人因可靠度状态转移Fig.1 State transfer of human reliability

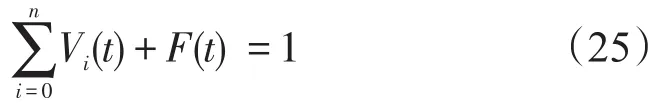
设某一PSF共分为n+1种程度，在t→t+Δt时间段内，PSF的第i种程度向第i+1种程度状态转移率为γi+1，向第i-1程度的状态转移率为 μi，而向其他状态的转移率为无穷小O(Δt)，列调继续保持在第i种操作成功状态转移率为V′i(t)，向操作失败的状态转移率为λi，即列调人因失误的概率Pr(FT).因此，构建第i种状态下的状态转移方程为

对于上述偏微分方程，进行拉普拉斯变化，转化为常微分方程：

求解出s的多重根，进行反拉式逆变换，即可得到几种状态下调度员的可靠性变化规律.

4 设置列控限速任务人因可靠性分析

列控限速是高铁调度指挥中常见的非正常情况，高速列车遇有自然灾害、恶劣天气、线路等设施故障或施工需要时，列调大多是以执行列控限速，降低列车运行速度来实现对行车的调整.列控限速命令的设置包括CTC系统参数设置、调度命令下达及列控限速设置等操作，涉及到调度指挥系统、列车运行控制系统、CTC系统等多个关键系统，列车限速设置将直接关系到列车的运行安全.因此，列控限速设置是高速铁路行车调度人因可靠性分析最具代表性的情景.基于此，本文以列控限速设置为例，进行列调人因可靠性分析及方法的可行性验证.而对于其他调度决策情景，如：列车运行顺序、变更列车停站等相对来说作业过程和作业环节要简单一些，其调度人员人因可靠性分析的方法和流程与列控限速设置是相同的，在此不再赘述.

列调设置列控限速的流程如图2所示.在此基础上绘制列控限速事件树（见图3），其中Xi表示动作单元i失败，xi表示动作单元i成功，S表示任务执行成功.依据人因失误手册，查找每一个动作标准失误率，通过现场调研和征求专家意见确定动作关联度，得到各动作单元的最终失误概率及概率置信区间，详见表1.

图2 任务操作流程Fig.2 Operation process of task

图3 设置列控限速时人因事件树Fig.3 Human error tree on setting speed limitation

表1 列调人因失误相关参数Table 1 Related parameters about human error

由式（3）、式（4），得到一级动作失误发生率和任务总失误率，详见表2.

表 2 失误事件概率Table 2 Failure probability

由式（15）～式（18），求得任务总失误概率所服从的对数正态分布参数 μlnPr(FT)、σ2lnPr(FT)，由式（8）～式（10），分别得到任务总发生概率的中值MPr(FT)、95%置信边界UPr(FT)及5%置信边界LPr(FT)，数值如表3所示.

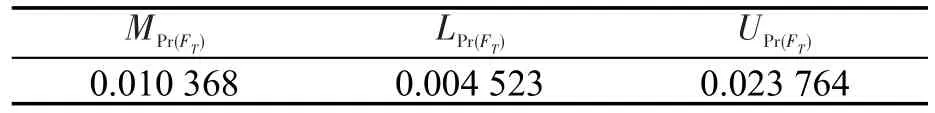
表 3 压力适中条件下任务失误概率中值及置信区间Table 3 The median and confidence interval of failure rate

在分析影响因子的作用时，分别选取压力低、适中、中高和极高（PSF分别取：2，1，2，5）四种情况计算列调人因失误率及90%的置信区间.由图4可知，列控限速命令的执行过程中，当压力超过适中压力值后，工作压力越大，操作失误的可能性越大，当压力低于适中压力值时，人因失误率也会增大.

图4 列调执行列控限速时的静态失误率Fig.4 Failure rate about setting speed limitation in static state

在已知压力影响下，列调操作失误及状态转移率的情况下，根据动态人因可靠性分析模型，分析列调在当班过程中压力适中V0(t)、压力中高V1(t)及压力极高V2(t)三种状态下成功完成任务的状态概率及三者动态转移情况.建立状态转移方程，由图4得λ0=0.010 4,λ1=0.020 5,λ2=0.023 4，γ1=0.04,γ2=0.1，μ1=0.06,μ2=0.15.假设系统初始状态：V0(0)=1,V1(0)=0,V2(0)=0，得出三种状态的概率变化趋势如图5所示.

图5 列调设置列控限速动态可靠性Fig.5 Dynamic reliability on setting speed limitation

从图5可知，随着工作时间的增加，压力较高时系统中列调可靠度的状态概率会增加，而压力适中时可靠度状态概率会降低.可见，随着工作时间的推移，列调处于适中压力条件下执行任务的状态概率要远高于压力中高和压力极高的情况，其中压力极高下的状态概率最小.

5 研究结论

本文结合高速铁路列调工作的特点，将工作任务划分为若干个动作单元，基于THERP理论，采用定量的方式得出列调静态人因失误概率.再引入马尔科夫链理论，建立人因可靠状态转移方程，分析列调可靠性动态转移规律.通过对列控限速任务的实例分析得到，在压力适中的情况下列控限速失败的概率为0.010 4，90%置信区间为（0.004 5,0.023 7），得到了不同压力情况下的人因可靠性变化规律.

同时，本文也存在一定的局限性：研究方法仅考虑了单一影响因子变动下，某一任务人因可靠性的变化规律，但在实际工作中，影响人因可靠性的因子可能有多个变动，因此多因子的变动将作为后续研究的重点.

[1] Swain A D,Guttmann H E.Handbook of human reliability analysis with emphasis on nuclear power plant applications[R].NUREG∕CR一1278,1983.

[2] Brune R L,Weinstein M,Fitzwater M E.Peer-review study of the draft handbook for human-reliability analysis with emphasis on nuclear-power-plant applications[R].NUREG∕CR-1278.Human Performance Technologies,Inc.,Thousand Oaks,CA(USA),1983.

[3] Kirwan B.The validation of three human reliability quantification techniques—THERP, HEART and JHEDI:Part 1—technique descriptions and validation issues[J].Applied Ergonomics,1996,27(6):359-373.

[4] Hollnagel E.Human reliability assessment in context[J]. Nuclear Engineering and Technology,2005,37(2):159.

[5] Taylor-Adams S,Kirwan B.Human reliability data requirements[J].International Journal of Quality& Reliability Management,1995,12(1):24-46.

[6] Cooper S E,Bley D C,Parry W G,et al.Knowledgebase for the new human reliability analysis method[C]∕∕A Technique for Human Error Analysis(ATHEANA), 1996.

[7] 张力.概率安全评价中人因可靠性分析技术研究[D].湖南大学,2004.[ZHANG L.The research on human reliability analysis technique in probabilistic safety assessment[D].Hunan University,2004.]

[8] 苏畅,张恒喜.飞机作战效能评估中人的可靠性的引入方法[J].航空学报,2006(02):262-266.[SU C, ZHANG H X.Method of considering human reliability in combat effectiveness evaluation of aircraft[J].Acta Aeronautica Et Astronautica Sinica,2006(02):262-266.]

[9] 张兴昌.列车调度员系统可靠性探讨[J].上海铁道科技,2011(01):22-23.[ZHANG X C.Reliability analysis of train dispatcher system[J].Shanghai Railway Science &Technology,2011(01):22-23.]

[10] 王洁,方卫宁,苗冲冲,等.地铁行车调度员人误模式结构化分析[J].人类工效学,2013(01):55-58. [ZHANG J,FANG W N,MIAO C C.Structured analysis on human mistake model of subway dispatcher[J]. Chinese Journal of Ergonomics,2013(01):55-58.]

[11] 王洁.面向地铁突发事件的行车调度系统人误预测研究[D].北京交通大学,2013.[WANG J.Research on traffic dispatching system human error prediction for the subway emergency[D].Beijing Jiaotong University, 2013.]

[12] 谢红卫,孙志强,李欣欣,等.典型人因可靠性分析方法评述[J].国防科技大学学报,2007(02):101-107. [XIE H W,SUN Z Q,LI X X,et al.An Overview of typicalmethods forhuman reliability analysis[J]. Journal of National University of Defense Technology，2007(02):101-107.]

[13] 刘卫华.利用THERP与HCR相结合的方法对秦山三期PSA人因可靠性进行修正[D].上海交通大学,2007.[LIU W H.Modification of human reliability analysis using HCR combination with THERP In third Qinshan Npp Psa[D].Shanghai Jiaotong University,2007.]

[14] Marvin Rausand.Risk assessment theory,methods,and application[M].Wiley,2011.

[15] Dhillon B S.Stochastic models for predicting human reliability[J].Microelectronics Reliability,1982,22(3): 491-496.

[16] Dhillon B S,Rayapati S N.Reliability evaluation of human operators under stress[J]. Microelectronics Reliability,1985,25(4):729-752.

Human Reliability Analysis on High-speed Train Dispatcher Based on THERP and Markov Theories

XU Pei-juan，PENG Qi-yuan,WEN Chao,GUO Jing-wei,ZHAN Shu-guang
（School of Transportation and Logistics,Southwest Jiaotong Universiy,Chengdu 610031,China）

In the dispatching system of high-speed railway,the dispatching terminal equipment is used by dispatchers who manage the running high-speed trains and related production activities,so reliability of dispatchers is directly related to the safety of high-speed trains.In this paper,THERP theory is introduced from nuclear plant industry to calculate the failure rate and the corresponding confidence intervals of dispatchers under static conditions,combining with the characteristics of their job content.According to the Markov chain theory,then the probability state transferring equations is established to study law of the dispatcher reliability under a certain influencing factor,by Laplace transform.Finally,the task about setting train speed limitation done by the dispatcher is taken for an example to analyze the static and dynamic reliability,when the person is under the influence of different level of pressure.The results show that human error rate about setting train speed limitation is lowest with 0.010 4 under medium pressure state.

railway transportation;human reliability;THERP theory;Markov chain;dynamic reliability

2014-04-15

2014-09-21录用日期：2014-10-08

国家自然科学基金（U1234206）；西南交通大学博士研究生创新基金（2015）.

徐培娟（1989-），女，山东聊城人，博士生. *

wenchao@swjtu.cn

1009-6744（2014）06-0133-08

U292.4+2

A