基于改进沙漏模型的突发事件下交通流预测

文江辉,江泽武,徐佳恒,张随远,毛树华

(武汉理工大学a.智能交通系统研究中心；b.理学院；c.物流工程学院；d.能源与动力工程学院；e.计算机科学与技术学院，武汉430063)

基于改进沙漏模型的突发事件下交通流预测

文江辉a，b,江泽武*c,徐佳恒d,张随远e,毛树华b

(武汉理工大学a.智能交通系统研究中心；b.理学院；c.物流工程学院；d.能源与动力工程学院；e.计算机科学与技术学院，武汉430063)

通过分析突发事故导致车道被占用时，道路通行能力的演变过程及交通流的变化特征，将占道发生后车流与沙漏模型中颗粒物质运动类比，结合突发事件下交通流中不同类型车辆的换道规律，提出了含概率崩塌各异性的改进沙漏模型.并结合元胞自动机仿真理论，运用MATLAB进行仿真计算不同时刻的车辆排队长度，与实际数据对比，该模型的平均相对误差为6.509 7%，验证了模型的可靠性.最后利用该模型预测不同车道被占用和不同车流量的情况下车队长度达到特定长度所需的时间，进而探讨其分别对道路通行能力的不同影响程度，为交通部门监管道路提供理论依据.

城市交通；改进沙漏模型；元胞自动机；突发事件；通行能力；排队长度

1 引 言

城市道路具有交通流密度大、连续性强等特点，一旦车道被占用，往往引起车辆排队、交通阻塞现象.正确预测车道被占用后道路通行能力变化情况，能为交通部门对事故处理、道路维修及停车位设置等方面提供理论依据.目前，国内外学者在交通预测方法方面已有不少研究，大致可分成三类：第一类是以数理统计等传统数学方法的线性预测模型，主要有时间序列法，自回归滑动平均模型和卡尔曼滤波预测模型等，但其考虑因素较为简单，依据数据线性变化趋势预测交通流参数，董春娇[1]等通过对实测数据的分析，提出了交通流参数模型，但该模型无法反映交通流的实际演变过程，在使用时也存在局限性；第二类是基于现代控制理论，以模拟技术、神经网络、模糊控制等为主要方法的非线性预测模型，李嘉[2]等基于交通数据融合技术提出了一种预测模型，在一定应用范围内具有良好的鲁棒性和精确度，但该模型对于大型路网的适应性还不能完全确定；第三类主要是前两者的组合应用，樊娜[3]等针对短时交通流变化周期性与随机性的特点，提出了新的混合预测模型，该模型预测精度高于单项模型单独预测时的精度，能较准确地反映交通流真实情况.

另一方面，Bak[4]等人提出了BTW(Bak Tang Weisenfeld)模型，对沙堆崩塌现象进行了计算机模拟.在此基础上本文以三车道为例，基于BTW沙堆演化进行改进，结合突发事件下交通流的基本特征，建立改进的沙漏模型，运用元胞自动机进行仿真计算不同时刻的车辆排队长度，并根据实地调查数据对方法的精度进行验证.

2 突发事件下道路通行能力的演变过程

一般而言，交通事故发生后，事故发生点所在截面会因为通行道路变窄产生瓶颈.从事故发生到事故影响结束一般可以分为三个阶段：事件检测与响应阶段、事件影响的加重及现场处理阶段、事件影响的持续阶段.事故发生后上游通行能力的变化如图1所示.

对于不同的上游车流量，事故发生至影响结束的三个阶段时间也会各不相同，直接以通行能力来衡量事件的影响程度并不合适.因此，选取车辆排队长度达到某一值L0（根据不同情况选取不同值，一般选取事发点至交通路口的距离）所需时间来衡量事故对道路通行能力的影响程度.

图1 事故发生后上游通行能力变化示意图Fig.1 Schematic diagram of changes in upstream traffic capacity after the accident

3 沙漏模型的概述

沙漏模型是根据真实沙漏演变过程，在BTW模型的基础上进行改进，并引入随机性崩塌和沙粒大小对崩塌概率等影响因素的一个数学模型.图2描述一个宽度为L，高度为h的二维沙漏模型：以底部开口为起始点，hn表示n格点处高度，Zn=hn-hn+1，Zn表示n格点处的局部倾角.zc(i)表示该系统中某个沙粒的临界高度差，可根据实际情况确定.沙粒的动力学过程可分为：

(2)沙粒的弛豫过程，若zn＞zc，沙粒按以下规则运动，=hn-1，=hn+1+1.其中带*表示沙漏下一时刻之后的值，不带*表示沙漏当前时刻的状态.

崩塌判据：

当zi＜zc(i)时，沙粒不发生崩塌(p=0)

当zi＞zc(i)时，沙粒发生崩塌(p=1)

当zi=zc(i)时，沙粒以概率p崩塌(0＜p＜1)

若有不同的格点均满足崩塌判据，采用并行的模拟顺序；若所有格点满足zi＜zc(i)，则状态保持不变.开口处竖直方向上一层沙粒落下到下一层沙粒落下的时间作为一个崩塌周期T，开口大小用R表示.

图2 二维沙漏模型图Fig.2 Two-dimensional hourglass model

该模型是基于BTW沙粒演化进行改进，提出的含概率崩塌的各异性沙漏模型.与小尺度的沙粒崩塌行为符合相当好，大尺度的沙粒崩塌几乎是周期性的，不同于该模型[5]，沙漏模型考虑到了沙粒的崩塌概率各异性，更加贴近真实沙漏的演化.

4 沙漏模型在突发事件下交通流中的改进及应用

现阶段的研究中，动力学模型难以体现微观上的车辆换道和跟驰的状态转移，Nash模型和STCA模型[6]对车辆设置的换道规则是单一不变的，其反映的是性格保守驾驶员的换道行为，无法再现实际交通的多样性.本文以交通事故为研究对象，分析在突发事件下通行车辆的颗粒性，建立改进的沙漏模型，预测事故后交通流的发展状况.

由李霖渊[7]的试验可知，沙漏模型中改变开口所处位置和开口占宽比R∕L(1∕6-1∕2)均能较好的符合演化规律，为交通流系统在突发事件下车道堵塞2/3的模型化提供理论依据.同时沙粒在沙漏中的运动与车辆在车道中的运动如图3所示有四点共性：

（1）沙漏的玻璃壁对沙粒运动的限制与车道边缘对车辆行驶的约束类似.

（2）部分车道被占用时，车辆的通行会受到影响，在车流量足够大的情况下，一段时间后事故截面处的车流量会达到饱和，此时车辆之间的间隙达到临界值，车辆的流动出现连续性，这规则与沙粒因重力而产生的系统连续性契合.

（3）当车辆前面遇到障碍且毗邻车道有足够的空位时，车辆会以一定的概率p进行换道，与沙漏模型中沙粒的随机崩塌过程类似.其中换道概率p与毗邻车队长度差正相关，也和驾驶员个人习惯相关.

（4）假设车辆在排队过程中，从一个状态转移到另一毗邻状态的时间为T，该时间与沙漏模型中的崩塌周期类似.

图3 车辆排队与沙漏的映射图Fig.3 Mapping between vehicle queuing with the hourglass

(2)车辆的跟驰过程.

如果sin足够小，在计算机随机模拟下该车不换道，使得

(3)车辆的换道过程.

如果第i个车道的第n辆车的换道概率较大，发生换道行为，分靠左换道和靠右换道两种情况：

式中 带*表示车流系统下一时刻之后的值，不带*表示车流系统当前时刻的状态.

在一个周期内，交通路段车辆随机驶入.对于每辆车的跟驰或换道过程，采用并行的原则，按照换道概率p进行随机模拟，交通流相关参数设定如下.

(1)等效车长ak和状态转移周期T.

等效车长的设定有两种方法：一是根据交通运动学理论进行计算，二是实地考察，结合观测数据设定.本文研究的是交通流在突发事件下的情形，不满足方法一的使用条件，故采取方法二对等效车长进行设定.状态转移周期T指由某一状态转移到另一毗邻状态间的时间差，其设定方法与等效车长类似.

(2)换道概率p.

突发事件引起的特殊交通流中，从t时刻到t+1时刻，车辆有两种行驶状态，跟驰行驶或变道行驶.当竖直高度差为0时，车辆没有空间进行换道，换道概率为0；随着竖直高度差与车辆本身长度比值的增大，换道的概率也变大，另外p与驾驶员的倾向有关.基于此，建立车辆换道概率的隶属度函数为

式中 δ为驾驶员倾向系数，取0.8-1.2；a,λ为模型参数，根据路况和车流量确定.p随sin∕ak的函数关系如图4所示.

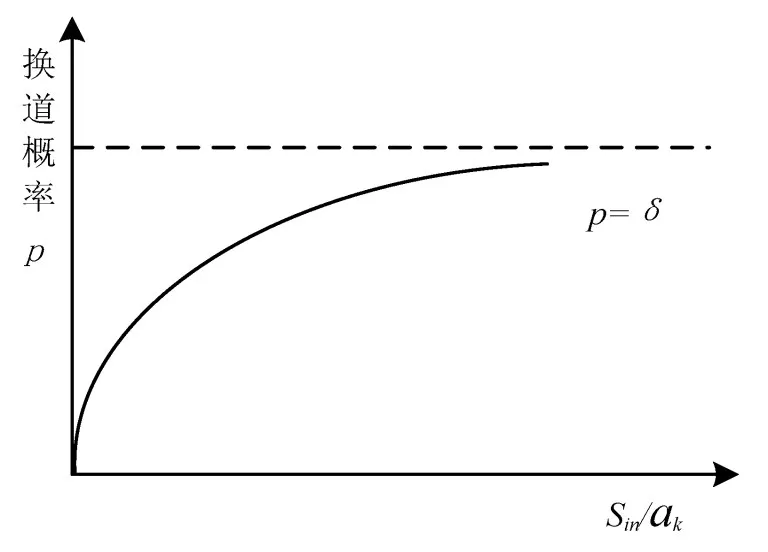
图4 车辆变道概率-隶属度函数曲线图Fig.4 Probability of vehicle's lane-changing the membership function graph

图4所示的曲线表明，换道概率随着sin∕ak变大呈增大趋势，最大值为1.曲线刚开始上升较快，当换道概率达到一定的值后，上升趋势变缓，符合实际交通流中车辆换道概率的规律.

(3)车辆驶入参数.

交通系统中t时刻到达某一横截面的车辆数服从泊松分布，即

其中第i个车道每辆车到达队列时间的期望值为

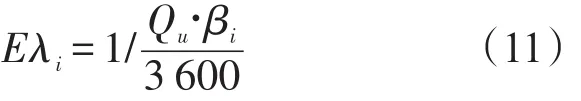
式中 βi为第i个车道的需求比；Qu为上游的车流量.

当某个车道排队堵塞至上游十字交叉路口时，就会对该交通路段造成严重影响，甚至引起交通瘫痪.因而，车辆排队的有效长度为三个车道中最长的车队长度，即

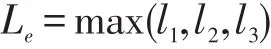
上述为基于改进沙漏模型的突发事件下车辆行驶过程分析与建模，一方面对车辆的驶入、换道、等候和驶出进行了分析，另一方面，对车队的长度和变化进行了分析.根据以上模型，能得出车辆排队长度与时间之间的关系.

5 案例分析与数值计算

根据上述建立的改进沙漏模型和车辆行驶的规则，运用元胞自动机[8]进行随机模拟及数值计算，结合实际交通堵塞的案例进行验证，并对不同占道方式产生的影响进行对比分析.选取2013年2月26日17:28:52-18:04:10某城市道路发生交通事故后一段时间的视频，该道路的基本参数如图5所示.

图5中数据及视频资料显示，该路段车道宽度为3.25 m，事故发生地离上游路口为240 m，车道需求比 β1:β2:β3=21%:44%:35%，上游路段车流量为1 500 pcu/h，事故发生时车辆初始排队长度为零；依据公路工程技术标准[9]，道路的设计速度为30 km/h，普通小轿车和公交车的等效长度分别为10 m和18 m，平均状态转移周期T为3 s；驾驶员根据换道倾向分为保守型、一般型和冒险型(δ分别取0.8、1.0、1.2)，模型参数a取0.5-1.0，λ取0.85-1.12.根据改进沙漏模型对车流仿真得到交通流动态演化过程，其中部分时刻的状况如图6所示.

运用改进的沙漏模型进行交通流预测，根据视频读取的数据，综合对比交通流模型[10]，结果如表1所示.

图5 发生交通事故的路段示意图Fig.5 Diagram of road segment in traffic accident

图6 发生事故到排队长度到达上游路口的车流动态演化过程Fig.6 The evolution process of traffic flow from the beginning of accident to the length of line arrives at upstream crossing

表1 交通流模型、改进沙漏模型与实际视频数据的对比Table1 The contrast of traffic flow model,sandglass model to real video data

上述计算结果表明，交通流模型与改进的沙漏模型均能较准确的预测车辆的排队长度，但运用改进的沙漏模型仿真计算得到的结果相对误差更小.另一方面，改进的沙漏模型能够更为透彻分析每辆车的转移过程以及堵塞车流系统的整体变化情况.

为了进一步探究实际生活中不同占道情况对车辆通行的影响程度，以广泛应用的三车道为例进行分析，运用改进的沙漏模型，得到在不同的车道被占情况下排队到上游路口的时间，实验结果如表2所示.

表2 不同的占道方式下堵塞至上游路口的试验Table 2 The experiments on congestion till upstream crossing in various ways of lane-occupying

根据以上结果，得到如下结论：

(1)占单车道情况下，上游车流量为1 500 pcu/h时车辆堵塞至上游路口所需的时间是车流量为3 000 pcu/h的2-3倍；

(2)对于占不同单车道的情况，理论上占中间车道影响最小，而实际上占1车道影响最小，与上游需求比相关；

(3)占单车道时车辆堵塞至上游路口所需的时间为占双车道的1-2倍.

另外，对于所选视频，当2、3车道被占用时，根据改进的沙漏模型求解，得到车队长度到达上游路口的时间为737 s，为了防止事故再次发生或者堵塞其他道路，相关部门应尽量在737 s内处理完该事故，如果在应急时间内不能解决事故，需采取其他措施来防止事故影响扩大.

6 研究结论

本文通过建立改进的沙漏模型将车流系统转化成沙漏系统进行研究，结合车辆排队、跟驰和换道等微观状态转移规律，运用元胞自动机原理进行仿真计算，能得出各种占道情况下的车辆通行状态.实例分析表明，相比交通流模型，改进的沙漏模型在突发事件下交通流预测中适用范围更广，同时提高了预测准确率.对于日趋成熟的智能交通系统，在突发交通事故的情况下，沙漏模型亦能为车辆选择合适的行车路线提供理论依据，该模型对于交通流非拥堵情况应用有待进一步研究.

[1] 董春娇,邵春福,等.基于实测数据的快速路交通流参数模型[J].交通运输系统工程与信息,2013,13 (3):46-52.[DONG C J,SHAO C F,et al.Estimating traffic flow models for urban expressway based on measurement data[J].Journal of Transportation Systems Engineering and Information Technology,2013,13(3): 46-52.]

[2] 李嘉,刘春华,胡赛阳,等.基于交通数据融合技术的行程时间预测模型[J].湖南大学学报:自然科学版, 2014,41(1):33-38.[LI J,LIU C H,HU S Y,et al.A travel time prediction model based on traffic data fusion technology[J].Journal of Hunan University:Natural Sciences,2014,41(1):33-38.]

[3] 樊娜,赵祥模,戴明,等.短时交通流预测模型[J].交通运输工程学报,2012,12(4):114-119.[FAN N,ZHAO X M,DAI M,et al.Short-term traffic flow prediction model[J]. Journal of Traffic and Transportation Engineering,2012,12(4):114-119.]

[4] Bak P,Tang C,Wiesenfeld K.Self-organized criticality: an explanation of 1∕f noise[J].Physical Review Letters, 1987,59(4):381-384.

[5] Held G A,Solina D H,Solina H,et al.Experimental study of critical-mass fluctuations in an evolving sandpile[J].Physical Review Letters,1990,65(9):1120.

[6] 赵康嘉，陈淑燕.基于元胞自动机的交通事件交通流仿真模型[J].公路交通科技,2014,31(003):133-138.[ZHAO K J,CHEN S Y.Cellular automaton based traffic simulation model for traffic incident[J].Journal of Highway and Transportation Research and Development,2014,31(003):133-138.]

[7] 李霖渊.沙漏计时原理二维数值模拟研究[D].贵阳：贵 州 大 学,2008.[LI L Y.The hourglass timing principle two dimensional numerical simulation research [D].Guiyang：Guizhou University,2008.]

[8] Kita E,Nanya W,Wakita Y,et al.Road network determination by cellular automata traffic flow simulation[C]∕Computing and Networking(CANDAR), 2013 First International Symposium on IEEE,2013: 500-504.

[9] 中华人民共和国交通部.JTG∕B01-2003公路工程技术标准[S].北京：人民交通出版社,2003. [Ministry of Communications and Transportation.JTG∕B01-2003 Code for technical standard of highway[S]. Beijing：China Communication Press,2003.]

[10] 纪英,高超.道路堵塞时排队长度和排队持续时间计算方法[J].交通与计算机,2009,27(Z1):41-43.[JI Y,GAO C.Method to calculate vehicle queuing length and queuing under crowded road[J].Computer and Communications,2009,27(Z1):41-43.]

The Forecasting of Traffic Flow Based on Optimized Hourglass Model in Emergencies

WEN Jiang-huia，b，JIANG Ze-wuc，XU Jia-hengd，ZHANG Sui-yuane，MAO Shu-huab
(a.Intelligent Transport Systems Center；b.School of Science;c.School of Logistics Engineering；d.School of Energy and Power Engineering；e.School of Computer Science and Technology,Wuhan University of Technology,Wuhan 430063,China)

From the analysis of the evolving of traffic flow when traffic congestion emerges caused by accident,analogies of traffic flow with the movement of particulate matter in hourglass model and various vehicles’lane changing pattern in emergency situation,an optimized hourglass model is propose.Based on cellular automata method,we simulate the queuing lengths of vehicles in different time on MATLAB and compare them with the practical data.We find that the average relative error of the model is 6.509 7%, verifying the reliability of the model.Finally,according to the model,we predict the time required for the specific queuing length on various lanes and traffic volumes.Thusly,we can study the impacts of time on traffic capacity and provide a theoretical basis for transportation administration.

urban traffic;optimized hourglass model;cellular automata;emergency;traffic capacity; length of queuing

2014-05-15

2014-08-01录用日期：2014-08-08

国家自然科学基金项目（61403288）；中国博士后科学基金（2014M562076）；中央高校基本科研业务费专项资金资助（2014-IV-080）.

文江辉（1986-），女，湖北松滋人，讲师，博士. *

JZW570585042@163.com

1009-6744（2014）06-0086-06

U491.3

A