随机投资收益率下带干扰的再保险风险模型
王丽霞,李双东,沈辰
(1.安徽大学江淮学院公共基础部,安徽合肥 230031;2.合肥师范学院数学系,安徽合肥 230060)
随机投资收益率下带干扰的再保险风险模型
王丽霞1,李双东1,沈辰2
(1.安徽大学江淮学院公共基础部,安徽合肥 230031;2.合肥师范学院数学系,安徽合肥 230060)
在经典风险模型的基础上,假定保费收入服从复合Poisson过程,将初始资金中多余的部分资本用于投资,结合金融市场的随机性,考虑投资收益率为随机变量的情形,并将通货膨胀等随机干扰因素的影响也考虑进来。同时,为减小风险,将模型以比例再保险策略控制,建立了带有随机保费收入、随机投资收益和随机干扰的再保险风险模型,使其更为符合实际。运用概率统计及精算方法得到模型破产概率的一般表达式及Lundberg不等式。最后借助MATLAB软件对结论进行了数值模拟,直观地说明了投资额、投资收益率、再保险自留水平对破产概率的影响.
随机收益;破产概率;比例再保险;数值模拟
引言
风险模型的再保险和最优投资策略的研究,是精算数学和保险业的热门话题,而经典风险模型的破产概率是学者们研究的主要对象①Gerber H U著.成世学:《数学风险轮导论》,严颖译,北京:世界图书出版公司,1997年。,随着保险市场的日益完善和竞争的日益激烈,经典风险模型已不能满足实际运用的需要,随之而来的便是对于经典模型的一系列改进。
Boikov②Boikov,A.V.,The Cramér Lundberg model with stochastic premium process.Theory of Probability and its pplications,2003,47,pp.489-493.假定保单收入过程为齐次复合Poisson过程,保费收入过程为一个随机过程,Wang③Wang,G.Wu,R,Distribution for risk process with astochastic return on investments.Stochastic process 2001.85.pp.329-341.和Yuen④Yuen,K.C.et al,Ruin probabilities for a risk process with stochastic return on investment.Stochastic Proc.Appl.,2004,110.pp.259-341.则考虑将多余的资本用于投资,以提高保险公司的赔付能力,聂高琴⑤聂高琴,刘黎明:《一类带干扰的双险种风险模型》,《统计与决策》2009年第17期,第160-161页。及黎锁平⑥黎锁平,刘琪:《投资和干扰具有随机保费的离散风险模型》,《高校应用数学学报》2009年第1期,第9-14页。将通货膨胀等随机干扰因素的影响考虑进来,得到了带干扰风险模型的最终破产概率的Lundberg不等式。赵金娥⑦赵金娥,王贵红,龙瑶:《理赔次数为复合Poisson-Geometric过程的风险模型》,《西南大学学报》(自然科学版)2013年第3期,第14页。假定理赔过程为复合Poisson-Geometric过程,李棵⑧李棵,赵晓芹:《多因素影响下的三非齐Poisson风险模型》,《数学理论与应用》2013年第1期,第77-81页。则考虑了保费收取及索赔过程均为非齐次Poisson过程,得到了类似的结果。本文假定保险公司将多余资本用于投资,由于投资种类的多样性、复杂性,当资产组合中的投资种类达到一定数量时,可假定资产组合的投资收益率服从正态分布。在此基础上考虑模型由比例再保险控制,再保险对于分散保险人的风险,增加保险公司的偿付能力有着很重要的作用,因此成为学者们研究的一个重要方向①Diasparra M A,Romera R,Bounds for the ruin probability of a discrete-time risk process,J.Appl. Probab.,2009.46.pp.99—112;Christian Irgens,Jostein Paulsen,Optimal controlof risk exposure,reinsurance and investments for insurance portfolios,Insurance:Mathematics and Economics 2004.35.pp.21–51; Liang Z.,Guo J.,Upper bound for ruin probabilities under optimal investment and proportional reinsurance, Applied Stochastic model in business and Industry,2007.23.pp.63-71.,然而在离散情形下的讨论则相对较少,本文在经典模型的基础上,既考虑了将多余资本投资到具有随机投资收益率的金融市场中,又将市场的干扰因素引入进来,为降低风险,以比例再保险的方式分散风险,使得模型具有更强的实践意义。通过对新模型的研究,得到了最终破产概率的Lundberg不等式及其一般表达式,随后利用MATLAB软件,对模型进行数值模拟,利用图形说明了投资额的大小、平均投资收益率,以及再保险的自留水平对调节系数的影响,获得了更有应用价值的结论。
1 模型的建立
在完备概率空间(Ω,F,P)上,定义如下模型:

其中Uo=u为保险公司的初始资金,Un表示保险公司第n期的盈余,对模型做出以下假设:
(1)F为依据保险公司的经营状况测算出的用于投资的资金,为一常数;{Ii,i>1},{Xi,i>1},{Yi,i>1}均为独立同分布的随机变量序列,Ii表示第i期投资收益,Xi和Yi分别为第i期的保费收入及赔付额,假定:Ii~N(μ0,σ02),且E(X1)=μ1,E(Y2)=μ2;
(2)M(n)和N(n)分别为时间段(0,n]内保险公司收到的保单总数和索赔总数,分别服从参数为λ1,λ2的Possion过程;
(3){Wn}是离散的Browaian运动,且当Δn很小时,E(Wn)=0,D(Wn)=n;
(4)假定变量{Ii,i>1},{Xi,i>1},{Yi,i>1},{M(n),n>1},{N(n),n>1},{Wn,n>1}相互独立.
模型中,函数h(b,y)为一个再保险策略,0<h(b,y)<y表示索赔额中由保险公司支付的部分,剩下的y-h(b,y)由再保险公司赔付。本文考虑比例再保险,即h(b,y)=by,其中b∈[0,1]为一常数,表示自留水平,当b=1,即为无再保险情形。C(b)为在自留水平b下,支付给再保险人的保费,由期望值保费原理:

注:当b=1,Ij=j时,即模型转化为文献[6]中的式子.为保证公司正常经营,假定E(Snb)>0,即Fμ0>bλ2μ2-λ1(μ1-C(b)),令

为原保险公司的安全附加系数.
2 主要结果
定义:破产时刻T=inf{n>1|Unb<0},最终破产概率ψb(n)=P(T<∞|U0b=u),则T为一停时。
定理1存在函数g(r)使得E[e-rSbn]=eng(r),且方程g(r)=0有唯一正解R,并称之为调节系数。


具有平稳独立增量性,根据模型假设知{Ii,i>1},{Xi,i>1},{Yi,i>1},{M(n),n>1},{N(n),n>1},{Wn,n>1}相互独立,且复合Possion过程和Brownian运动具有平稳独立增量性,易知结论成立。
下证(5)式成立。∨u>0,r>0由全概率公式知:


3 数值模拟
为直观地说明本文所得出的结论,本节利用MATLAB软件对模型的结论进行了数值模拟,简单起见,假定保费收入及索赔额服从指数分布。

(1)取θ=10%,σ02=0.012自留水平b=0.5,在投资平均收益率μ0分别取0.02及0.05时,得到投资额F与调节系数R的关系图(图1),由图1可以看出:Ⅰ.投资总额对保险人的经营状况有很大的影响,但在收益率随机的情形,并非投资数额越多越好,只有恰当地选择最佳投资额(图中峰值的位置),才能使破产概率的上界最小;Ⅱ.不同的投资收益率影响着投资金额及破产概率上界:平均收益率越大,调节系数越大,相应的破产概率上界越小,最佳投资额也相对偏大.

图1 投资额F与调节系数R的关系
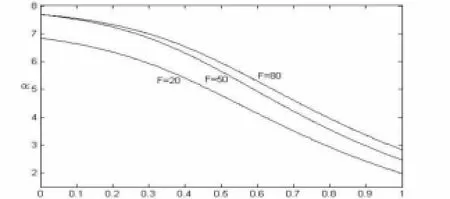
图2 自留水平b与调节系数R的关系
(2)取定μ0=0.05,在投资额不同的情形分别得到自留水平b与调节系数R的关系(图2),图2表明破产概率上界随自留水平b的增大而增大,这说明再保险对保险公司的经营状况至关重要,而同一自留水平下,不同的投资额对调节系数的影响也不一样,因此投资额的选择不仅跟当前的投资收益率有关,还应以自留水平作为重要的参照。
4 结束语
本文对学者们推广的经典风险模型进行了更深入的研究,不仅考虑了随机投资收益率,且将模型运用比例再保险进行控制,大大加强了模型的实用性,利用数值模拟让结论更直观,但本文所研究模型还可以做更进一步的推广,例如考虑模型的随机利率以及不同的保费收取过程和索赔过程等。
A reinsurance risk model with interference under random return on investment rates
WANG Lixia,LI Shuangdong,SHEN Chen
An improved model based on the classical risk process is established,it is assumed that premium income is modeled by a compound Poisson process,and the surplus capital is invested,with the randomness of the financial market,the return rate of the investment is considered as random variables,and inflation in insurance business is also taken into account in the model.In order to reduce the risk,the model can be controlled by proportional reinsurance which made the model more practical.Then the formulas of ultimate ruin probability and Lundberg inequality for the improved model are obtained.To illustrate these results,some numerical examples are included by using the software of MATLAB.The influence of the amount of investment,the rate of return on investment and reinsurance retention level on the upper bound of ruin probability is intuitive illustrated.
random income;ruin probability;proportional reinsurance;numerical simulation.
F224.7
A
1009-9530(2014)05-0065-04
2013-09-17
安徽大学江淮学院科研基金项目“比例再保险风险模型的研究”(2012KJ1002),合肥师范学院产学研教育课程项目“金融数据搜集与分析”(2012CXY11)
王丽霞(1984-),女,安徽大学讲师江淮学院讲师,主要研究方向:风险精算理论。

