基于有限元法的隧道-坡体耦合稳定性分析
翟玉华
(张石高速公路张家口管理处,河北 张家口 075100)
0 引言
张家口至石家庄高速公路二期工程是河北省“十一五”期间的重点工程项目,是河北省高速公路布局规划“五纵、六横、七条线”公路网主骨架中“五纵”的重要组成部分。线路穿越路段地貌单元主要为桑干河盆地—蔚县盆地区低山丘陵单元和蔚县南部中山区单元,出现了大密度的路堤边坡、隧道工程,共有16座隧道,其中北口隧道为隧道群的门户。因受整体线路选择和特殊地形的限制,北口隧道位于坡体上并且两洞口间沿行车方向修筑125m长的路堤工程。其进口段工程的稳定性不仅关系到北口隧道的施工进度,而且影响到张石高速整个工程的成败。因此,有必要对隧道进口段坡体不同工况下(隧道开挖后-隧道支护后-路堤修筑后)的稳定性进行分析。
目前对于边坡和隧道工程的稳定性分析,国内外工程实例较多[1-3],相关研究多以独立单位进行分析,而将其两者作为整体研究的文献很少[4-6]。数值分析法以其既能定性又能定量分析工程问题的优点,近年来受到广大学者的青睐。本文基于有限元理论,运用MIDAS/GTS软件建立了原始边坡-隧道-路堤边坡三者耦合的仿真三维分析模型,对北口隧道进口工程不同工况下坡体的稳定性进行了分析,得出了隧道开挖和路堤修筑过程中原始坡体位移和应力的变化规律,验证了初期支护参数和施工方法的合理性。
1 隧道-坡体耦合稳定性分析三维模型
1.1 模型设计
1.1.1 本构模型
根据应力-应变关系的不同,弹塑性材料大体可分为三大类:理想弹塑性材料、应变硬化材料、应变硬化-软化材料。岩土介质可归属为第二、第三类材料。目前工程中通常采用4种屈服准则,即屈雷斯卡(Tresca)、范米赛斯(Von Mis⁃es)、莫尔-库伦(Mohr-Coulomb)、德鲁克-普拉格(Drucker-Prager)准则。其中前两种适用于金属类材料,后两种适用于岩土类材料。Drucker-Prager准则属于能量屈服与破坏准则,其优点是考虑了中间主应力σy对屈服与破坏的影响,屈服曲面光滑没有棱角,克服了Mohr-Coulomb准则的主要弱点。本文选择德鲁克-普拉格(Drucker-Prag⁃er)准则进行模拟计算。
1.1.2 模型尺寸选定
在有限元计算中,边界约束条件对计算结果影响较大,因此应尽量减少有限元模型中边界约束条件对计算结果产生的不利影响,尽量使边界条件和实际情况相符,并使计算模型足够大,使分析的重点区域处于模型的中央部位,以减小边界效应。依据弹塑性理论和工程类比,计算模型范围的选取通常由隧道跨度和高度确定:外边界左右取跨度的3~5倍,上下取高度的3~5倍,在所取范围之外可认为不受开挖等施工因素的影响,即在这些边界处可忽略开挖等施工所引起的应力和位移。同时,保证模型不出现刚体位移及转动。
根据隧道既定路线及地质条件,衬砌断面内轮廓采用三心圆方案,隧道净高7.8m,单洞净宽13.25m,横断面组成为:(0.75+0.5+3.75×2+3.5+1.0)m,建筑限界高度为5.0m。现将模型数值解析区域设为:左、右各取50m,即隧道直径的4倍左右;在竖向向下取45m,即隧道高度的6倍,向上取至地表面,隧道纵向取长度为60m的V级围岩浅埋偏压段进行模拟。
1.2 参数设计
北口隧道进口段地层主要由黄土层、风化带、强风化白云岩三种地层组成,属于偏压段施工,因此支护参数设计采取了非均匀支护。从施工简单、便捷的角度考虑,提高钢架和喷射混凝土的刚度实现起来难度较大,而从锚杆入手相对来说比较容易。隧道内侧锚杆支护采用直径为25mm的中空注浆锚杆,长6.0m,间距为80×65cm;隧道拱顶锚杆支护采用直径为25mm的中空注浆锚杆,长4.0m,间距为100×65cm;隧道外侧锚杆支护采用直径为25mm的中空注浆锚杆,长3.5m,间距为100×65cm。钢架和喷射混凝土参数见表1。

表1 隧道支护参数
本文采用等参三维四面体结构单元模拟围岩,采用D-P模型,隧道结构周边围岩用线性梯度对称划分细密单元以提高计算精度;注浆加固区按经验采取提高围岩的黏聚力c和内摩擦角φ值加以模拟;取平面板单元模拟一衬,采用植入式桁架模拟系统锚杆,支护结构按弹性设置。地层实体单元和支护参数如表2~表4所示。

表2 实体单元计算参数
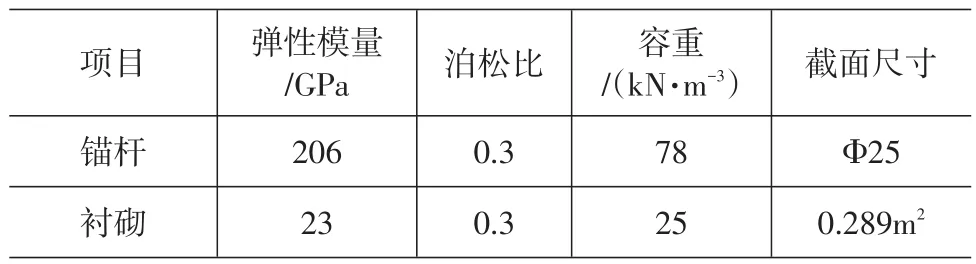
表3 梁、杆单元计算参数

表4 注浆加固区参数
1.3 模型建立
本文以实际地质地形图等高线为基础数据,运用MIDAS/GTS中的TGM(地形生成器)生成实际自由地表面,更加直观精确地反映隧道浅埋偏压的特点,然后建立三维模型进行模拟。地形生成与三维建模建立过程见图1。

图1 三维建模示意图
因隧道埋深浅且无构造节理影响,故地应力按初始自重应力场考虑。在模拟过程中,第一步为围岩初始应力场计算。隧道开挖前围岩处于初始应力状态;开挖后由于应力重新分布和局部地壳残余应力的释放,围岩产生位移形成松弛,达到新的暂时平衡状态,称为二次应力状态;支护后的隧道周边应力状态称为三次应力状态。这一力学过程通常采用“荷载释放系数”来模拟。荷载释放过程为:当前施工开挖段围岩释放40%荷载,随后的两个施工段依次释放30%的荷载。

图2 不同工况下位移场分布图
计算时施加的边界约束条件是:地表为自由边界,未加任何约束;计算模型的前后边界分别受Y轴方向的位移约束,左右边界受X轴方向的位移约束,模型的下部边界受Z轴方向的位移约束。
2 隧道-坡体耦合稳定性分析
2.1 计算步骤
模拟计算按隧道设计开挖步骤进行:上断面开挖→左下断面开挖→右下断面开挖。每次开挖2m,初期支护紧跟每步开挖之后,上断面、左下断面、右下断面之间的间隔距离为6m。隧道开挖完毕后进行路堤修筑。
2.2 结果分析
模拟计算后提取了各工况下的位移场(如图2所示)和应力场图形,并进行了分析。
2.2.1 位移场分析
(1)上断面开挖初期支护后
从图2(a)可以看出,上断面开挖完毕初期支护后,X轴方向正向位移最大为9.16mm,出现在隧道进口段坡体中间部位及进口处,坡面大部分水平位移范围在1.40~6.06mm之间,发生在隧道拱腰对应的坡面位置;Y轴方向正向位移最大为0.55mm,位移很小;Z轴方向坡面都为负值,最大值所在隧道拱顶对应的坡面位置范围为11.67~15.74mm,坡面位移由拱顶对应坡面位置向两侧变小,坡顶范围多些,位移范围在0.84~11.67mm之间。隧道上断面开挖初期支护后对坡面X轴方向、Z轴方向产生了一定的影响。
(2)左下断面开挖初期支护后
从图2(b)可以看出,左下断面开挖完毕初期支护后X轴方向正向位移最大值出现在隧道进口段坡体中间9.46mm增加了0.3mm,坡面大部分水平位移发生在隧道拱腰对应的坡面位置为1.39~6.23mm之间;Y轴方向正向位移最大值出现在隧道内侧拱腰对应的坡面位置为0.60mm处,增加了0.05mm;Z轴方向位移最大值发生在隧道拱顶对应的坡面位置,位移范围为11.93~16.27mm,增加幅度为0.26~0.53mm,坡面位移由拱顶对应坡面位置向两侧变小,坡顶影响范围增大。隧道左下断面开挖初支后对坡面的X轴方向、Z轴方向较上断面开挖初期支护后产生了稍大的影响,在坡顶位置变化明显。
(3)右下断面开挖初期支护后
从图2(c)可以看出,右下断面开挖完毕初期支护后X轴方向正向位移最大值为9.72mm,增加了2.6mm,隧道拱腰对应的坡面位置位移范围为1.44~6.41mm,增值范围为0.05~0.18mm;Y轴方向正向位移最大值为0.65mm,增加了0.05mm;Z轴方向位移最大值发生在隧道拱顶对应的坡面位置,位移范围为12.52~16.60mm,增加幅度为0.59~0.33mm,坡面位移由拱顶对应坡面位置向两侧变小,坡底影响范围增大。隧道右下断面开挖初支后对坡面的X轴方向、Z轴方向与较下断面开挖初期支护后位移有增大的趋势,在坡底位置变化明显。
(4)路堤修筑后
从图2(d)可以看出,路堤修筑后X轴方向正向位移最大值为65.11mm,发生在路堤对应的坡脚位置,隧道对应的坡面位移范围为2.00~8.85mm;Y轴方向隧道对应的坡面位置位移最大值为0.58mm;Z轴方向位移最大值发生在路堤对应的坡面坡顶位置位移最大值为68.67mm处,隧道对应的坡面位移范围为9.30~17.6mm。路堤修筑后对路堤接触坡面影响较大,对隧道对应的坡面影响较小,在一定意义上还起到了重力挡土墙的作用。
根据不同工况的位移云图结果分析可以看出,隧道进口段施工对坡体的位移有一定的影响,主要是X轴正方向和Z轴负方向位移,最大的坡面变形为17.6mm,为隧道边坡的竖向(Z轴负方向)变形,其次为边坡横向位移值9.72mm,如图3所示。从位移云图中还可看出,隧道开挖初期支护过程中,隧道周边围岩总的移动趋势为拱顶下沉,两侧边墙张开,底部仰拱向上移动,同时隧道对应的坡面位移在拱顶部分形成一个类似于“V”槽形状的区域,位移值均控制在允许范围内。
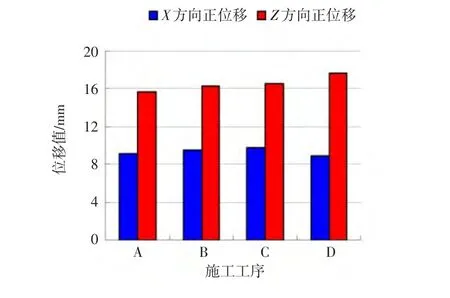
图3 隧道施工引起坡体位移变化规律
2.2.2 应力场分析
不同工况下分析模型三方向应力场分布如图4所示。

图4 不同工况下分析模型三方向应力场分布图
(1)上断面开挖初期支护后
从图4(a)可以看出,上断面开挖初期支护后SXX方向的最大值为1.27MPa,发生在坡体底部,为压应力;最小值为0.009 8MPa,为拉应力,发生在隧道底部仰拱和两侧拱腰及外侧拱腰对应的坡面位置。SYY方向最大值为0.66MPa,发生在坡体底部,为压应力;最小值为0.005 2MPa,为拉应力,发生在隧道底部仰拱和两侧拱腰及外侧拱腰对应的坡面位置。SZZ方向最大值为1.61MPa,发生在坡体底部,为压应力。坡面均受压应力值为0.004 1MPa。
(2)左下断面开挖初期支护后
从图4(b)可以看出,左下断面开挖初期支护后SXX方向最大拉应力和压应力值变化较小,只有隧道外侧拱腰对应坡面范围有所增大;SYY方向最大压应力值和位置基本没有变化,坡面均为压应力;SZZ方向最大压应力和坡面压应力和发生位移变化不大。
(3)右下断面开挖初期支护后
从图4(c)可以看出,右下断面开挖初期支护后SXX、SYY、SZZ三个方向最大拉应力和压应力值变化较小,只有SYY坡面压应力有所增大。
(4)路堤修筑后
从图4(d)可以看出,路堤修筑后,与路堤接触的坡面SXX、SYY、SZZ三个方向的应力值变化较大,隧道对应的坡面SYY、SZZ两个方向变化较小,SXX方向隧道仰拱、拱腰及其对应的坡面压应力值有所变小。
从以上几种工况各个方向的坡体地层主应力云图可以看出,整个地层大部分区域都是受压的,只是在隧道仰拱、拱腰及其对应的坡面附近很小的区域范围内出现拉应力,且随着工序的推进,整个地层的应力一直处于调整之中。
从隧道开挖初期支护后的坡体地层各方向的位移云图和应力云图分析结果可以得出,所采用的初期支护参数和开挖工法能够满足施工过程中围岩与坡体的稳定性要求。
3 结论
本文基于有限元理论,运用MIDAS/GTS软件建立了原始边坡-隧道-路堤边坡三者耦合的仿真三维分析模型。根据不同工况下分析模型三个方向的坡体地层位移云图计算结果,可得如下结论:
(1)隧道进口段施工对坡体的位移有一定的影响,主要是X轴正方向和Z轴负方向位移,最大的坡面变形为17.6mm,为隧道边坡的竖向(Z轴负方向)变形,其次为边坡横向位移值9.72mm。
(2)隧道开挖支护过程中,隧道周边围岩总的移动趋势为拱顶下沉,两侧边墙张开,底部仰拱向上移动,同时隧道对应的坡面位移在拱顶部分形成一个类似于“V”槽形状的区域,位移值均控制在允许的范围内。
(3)整个地层大部分区域都是受压的,只是在隧道仰拱、拱腰及其对应的坡面附近很小的区域范围内出现拉应力,且随着工序的进行,整个地层的应力一直处于调整之中。
(4)结合隧道开挖初期支护后的坡体地层各方向的位移云图和应力云图分析结果得出,所采用的初期支护参数和开挖工法能够满足施工过程中围岩与坡体的稳定性要求。
[1] SANAVIA L.Numerical Modelling of a Slope Stability Test by Means of Porous Media Mechanics[J].Engineering Com⁃putations,2009,26(3):245-266.
[2] Park K H,Tontavanich B,Lee J G.A Simple Procedure for Ground Response Curve of Circular Tunnel in Elastic-Strain Softening Rock Masses[J].Tunneling and Under⁃ground Space Technology,2008,23(2):151-159.
[3] Wang Xu-hua,Chen Shou-yu,Tang Lie-xian,et al.Appli⁃cation of Fuzzy Optimal Selection of Similar Slopes to the Evaluation of Slope Stability[J].Journal of Harbin Institute of Technology:New Series,2007,14(3):415-418.
[4] 王艳霞.模糊数学在边坡稳定分析中的应用[J].岩土力学,2010,31(9):3000-3004.
[5] 王军,曹平,林杭.受偏压隧道影响边坡加固的数值分析[J].公路交通科技,2009,26(9):102-106.
[6] 王建秀,朱合华,唐益群.连拱隧道-边坡耦合作用:连拱隧道滑坡[J].土木工程学报,2010,43(1):3785-3791.

