有限元法在斜拉桥应力分析中的应用
梁金华
(云南浩海建设集团有限公司,云南 昆明 650215)
0 引言
近年来,伴随着工程结构的复杂化、受荷形式的多样化及边界条件的日趋丰富化,依靠传统的经验法和解析法已不能达到对工程问题进行精确分析的目的。随着计算机在工程界的广泛应用以及计算理论和计算方法的发展,越来越多的专家、学者和工程师们开始应用数值分析方法来求解应用力学内的很多课题,并取得了显著的成果[1]。有限元数值分析方法因其高效、实用性强和精度高等优点,已成为一种应用于工程界各个领域的最广泛的计算方法。
1 有限元法
1.1 有限元的组成
有限元的基本构成包括节点、元素和自由度。
(1)节点(Node):是构成有限元系统的基本元素,是工程系统中点的坐标位置,具有其自身物理意义上的自由度。
(2)元素(Element):由节点与节点相互连接而成,元素的组合由各节点相互连接,不同特性的工程系统,采用不同种类的元素,ANSYS中提供了100多种元素,在使用时应根据需要选择元素的型号。
(3)自由度(Degree of Freedom):节点所具有的自由度,是工程系统受到外力后的反应结果。
1.2 有限元分析的基本概念和原理
用简单的问题代替复杂的问题而后再加以求解,是有限元分析的基本原则[4]。有限元分析将求解域看作是由多个称为有限元的互连子域组成,对每一个小的单元假定一个合适、简单的近似解,推导出求解域所要满足的总条件,从而得到问题的近似解。有限元法能将复杂的问题简单化,且计算精度高,因而成为比较有效的工程分析手段。
有限元法(Finite Element Method)是以变分原理为基础发展起来的,广泛地应用于以拉普拉斯方程和泊松方程所描述的各类物理场中。有限元法可应用于以任何微分方程所描述的各类物理场中,不再要求这类物理场和泛函的极值问题之间有所联系。其基本思路为:通过求解给定的泊松方程求得泛函的极值。
2 有限元法的应用——工程实例分析
2.1 工程概况
某桥主桥为独塔双索面预应力混凝土斜拉桥。主桥跨径为89.92m+89.92m,主桥全长179.84m。主桥平面位于直线上,立面位于0.42%的上坡上。结构形式采用塔梁墩固结的刚构体系,桥宽20m,主梁采用肋板式断面,塔柱采用空心矩形截面,斜拉索采用扇形布置。桥面以上塔高41.709m,为A型桥塔。
桥型布置如图1所示,主梁标准横断面布置如图2所示。
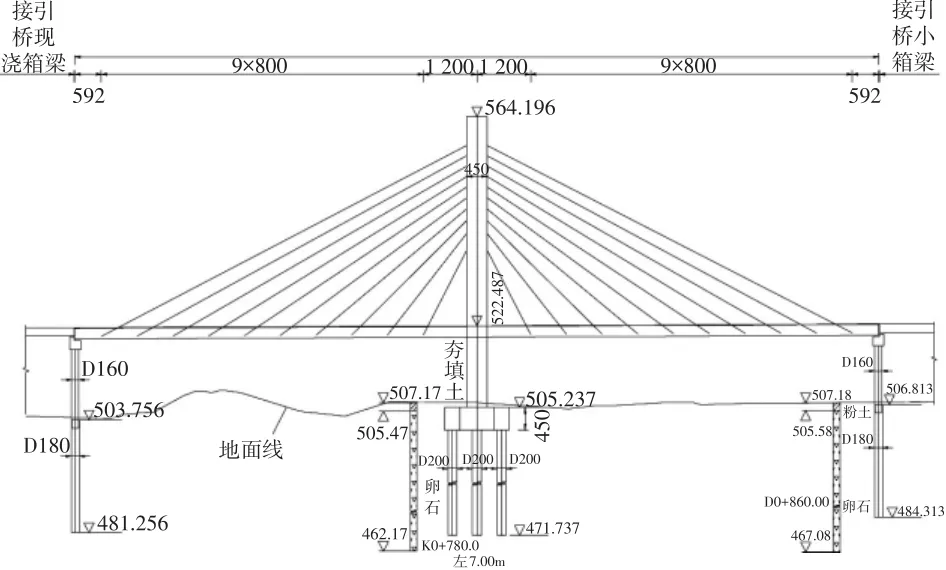
图1 桥型布置图(单位:cm)
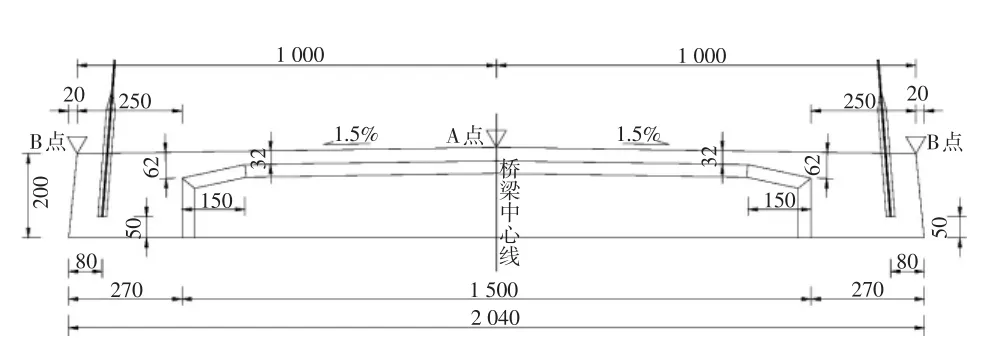
图2 主梁标准横断面(单位:cm)
2.2 有限元模型的建立
全桥共有225个节点,125个梁单元和40个索单元。其中斜拉索采用索单元模拟,主梁和主塔均采用Timoshenko梁单元模拟。边界条件为:不考虑桥墩基础与土之间的相互作用,在墩底固结。斜拉索与主梁和主塔之间的连接方式采用弹性连接中的刚性连接。全桥有限元分析示意图如图3所示。
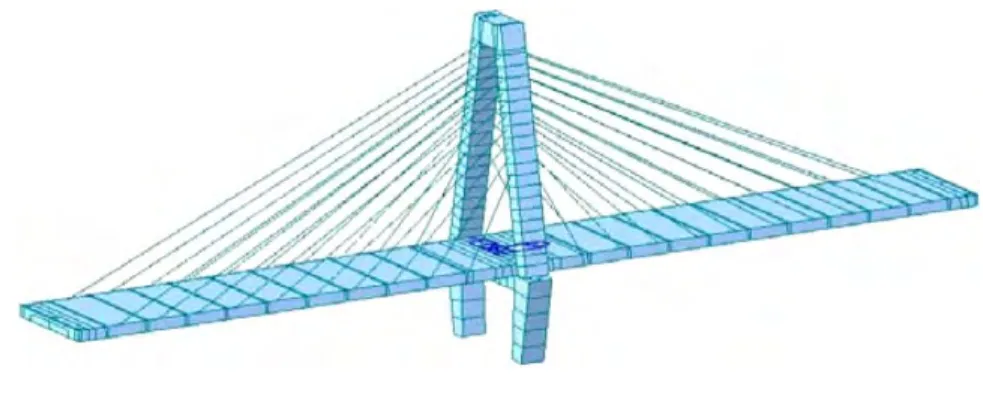
图3 全桥有限元分析图
2.3 有限元分析
对合龙后做完二期铺装和成桥后经历十年收缩徐变两阶段的主梁、主塔和斜拉索的应力进行分析,同时对主梁和主塔的变形进行分析。
2.3.1 主梁和主塔的应力分析
作用效应组合为[7]:恒荷载+施工荷载+钢束预应力荷载+因多余约束产生的预应力荷载+徐变实际内力+收缩实际内力。
(1)合龙后做完二期铺装阶段的应力分析(如图4所示)
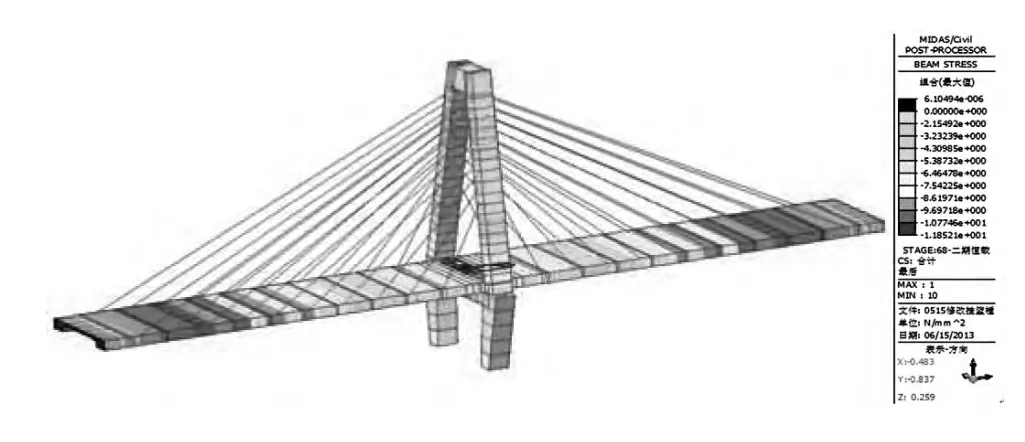
图4 二期铺装完成后的主梁、主塔应力图
由图4可知,主梁最大拉应力值为6.1×10-6MPa,最大压应力值为11.95MPa;主塔最大压应力为9.34MPa,最大拉应力为0MPa。由此可知,主梁和主塔的最大拉应力均满足规范要求,最大压应力均未超标,也满足要求。
(2)成桥后经历10年收缩徐变阶段的应力分析(如图5所示)
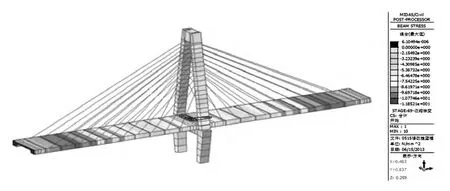
图5 10年收缩徐变完成后的主梁、主塔应力图
由图5可知,主梁最大拉应力值为6.1×10-6MPa,最大压应力值为9.49MPa;主塔最大压应力为9.23MPa,最大拉应力为0MPa。由此可知,主梁和主塔的最大拉应力均满足规范要求,最大压应力均未超标,也满足要求。
2.3.2 斜拉索的应力分析
作用效应组合为[7]:恒荷载+施工荷载+钢束预应力荷载+因多余约束产生的预应力荷载+徐变实际内力+收缩实际内力。
(1)合龙后做完二期铺装阶段的应力分析(如图6所示)
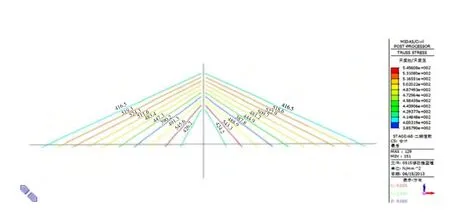
图6 二期铺装完成后的斜拉索应力图
由图6可知,斜拉索最大拉应力值为546MPa,最小拉应力值为388MPa。由此可知,斜拉索的应力分布较为均匀,最大拉应力满足施工阶段安全系数的要求,且均未超限。
(2)成桥后经历十年收缩徐变阶段的应力分析(如图7所示)。
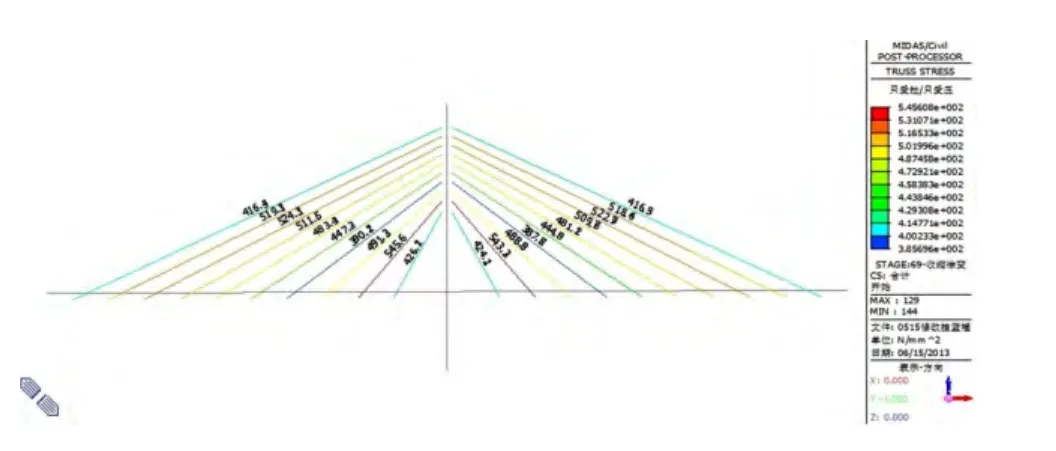
图7 十年收缩徐变完成后的斜拉索应力图
由图7可知,斜拉索最大拉应力值为547MPa,最小拉应力值为389MPa。斜拉索的最大拉应力均满足运营阶段安全系数的要求,且均未超限。
3 结语
在结构数值分析中解决工程问题的数值分析方法很多,其中以有限元法使用最为广泛。计算机技术的飞速发展使得有限元法的应用更加普遍与成熟,Midas Civil就是常用于桥梁结构中的专用有限元分析软件。本文结合某座独塔斜拉桥的施工阶段进行有限元分析,验证了通过Midas Civil可以对其施工阶段进行精确模拟,并且能够给出各阶段主要部件的准确响应,可为今后类似桥梁工程的求解提供借鉴。
[1] 钱家欢,殷宗泽.土工数值分析[M].北京:中国铁道出版社,1991.
[2] 龙驭球,龙志飞,岑松.新型有限元论[M].北京:清华大学出版社,2004.
[3] 夏永昶.板壳力学中的加权残值法[M].西安:西北大学出版社,1994.
[4] 骆利峰.高耸建-构-筑物爆破拆除倒塌过程中的动力学分析及计算机模拟[D].武汉:武汉科技大学,2004.
[5] 王文涛.斜拉桥换索工程[M].北京:人民交通出版社,1996.
[6] 顾安邦,范立础.桥梁工程下册[M].北京:人民交通出版社,2000.
[7] 邱顺冬,郑海霞,桂满树.桥梁工程软件Midas Civil[M].北京:人民交通出版社,2010.

