基于二极管的限幅蔡氏电路实验研究
闵富红,马美玲
(南京师范大学电气与自动化工程学院,江苏南京210042)
0 引言
蔡氏电路作为非线性电路中产生复杂动力学行为最有效、简单的混沌振荡电路,已经成为电路和物理实验教学中演示混沌现象的典型范例。传统的蔡氏电路结构简单,但在产生混沌现象时,元器件参数的可调范围却很小。另外,由于混沌系统对初始条件极为敏感,对电路中电感的精度要求很高,因此增加了电路实验的成本。许多学者通过对非线性部分进行重新设计,或者采用模拟电感替换实际电感等方法,对蔡氏电路进行了改进[1,2]。虽然上述方法取得了一定的效果,但增加了电路实验的复杂性。
本文基于蔡氏电路方程中系统变量之间的运算关系,利用运算放大器的限幅原理,设计合适的无感等效蔡氏电路。通过改变电位器的阻值来进行混沌现象的演示实验,获得周期、单涡卷及双涡卷等运动,获得的系统特性与蔡氏电路完全一致。此外,该硬件电路不仅结构简单,调试方便,而且能够直接从系统引出三个状态量,便于学生从示波器直接观测系统的运动,这为今后系统的混沌控制与同步应用等带来了很大的方便。
1 蔡氏电路模型
蔡氏电路存在的非线性环节是系统运动轨迹发生变化的主要原因。该非线性环节为2分段函数,因此系统主要存在2个运动轨迹的吸引域,一般有单涡卷和双涡卷两种混沌运动状态。蔡氏电路数学模型为[3-5]:

其中,h(x)=m1x+0.5(m0-m1)(|x+1|- |x-1|)。α,β,m0和m1为决定混沌电路运动状态的系统参数,基于Matlab软件仿真平台,我们选择ode45算法,改变系统参数,可以获得周期极限环和混沌吸引子等丰富的动力学行为。当选取m0=-1/7,m1=2/7,α=10,β=15时,蔡氏系统处于双涡卷混沌运动状态,相平面图和时序波形图如图1所示。

图1 双涡卷蔡氏混沌系统的相位图与时序图
2 蔡氏电路等效电路设计
蔡氏电路中的非线性环节是混沌产生的关键,也是电路设计的难点。传统蔡氏电路结构简单,包含一个电感、两个电容、一个电阻和一个非线性电阻[3],如图2所示。由于混沌电路本身对初始条件极为敏感,在实际电路实验中对电感的精度要求很高,利用示波器很难捕捉到稳定的混沌吸引子。因此,传统的蔡氏电路不易进行硬件实验制作,电路调试较为困难。
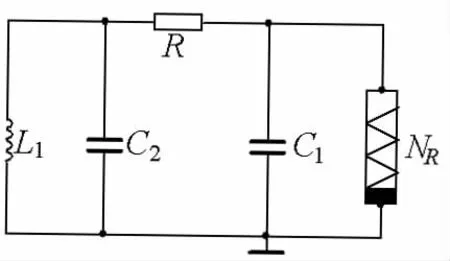
图2 经典三阶蔡氏电路图
下面对蔡氏电路方程进行逆向推导,得到不含电感的等效蔡氏电路。为了叙述方便,将式(1)改写成如下格式:

其中,f(x)=0.5(|x+1|- |x-1|)即:

分段函数f(x)的最大值不超过1,最小值不低于-1,具有限幅功能,保证了电路中混沌吸引子维持在局部区域内稳定运行。
对于该段具有限幅功能的非线性环节,设计的电路如图3所示。
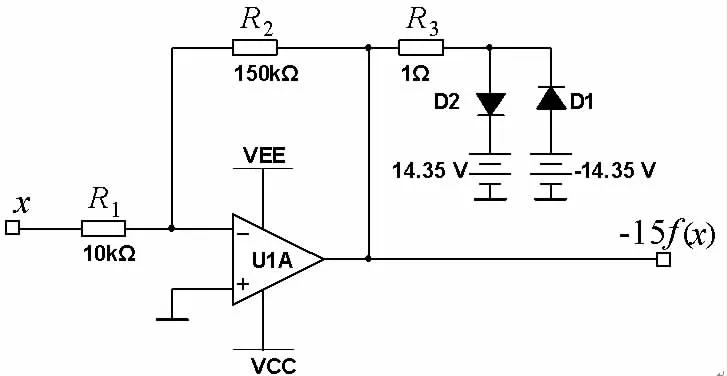
图3 限幅函数功能的电路图
该限幅函数电路由一个运放U1A、三个电阻R1,R2,R3,两个二极管以及正负直流电源来实现。电路中运放选用芯片TL082CD;两个二极管D1和D2型号为1N5712,其导通电压约为0.65V。它与±14.35V的工作电压及R3(1Ω)的电阻连接后,加在运放的输出端,使得其输出电压钳制在15V之间,实现了限幅电路的功能。若运放输入端为x,那么输出端Vo为

选取电阻R1=10kΩ,R2=150kΩ,上式简化为
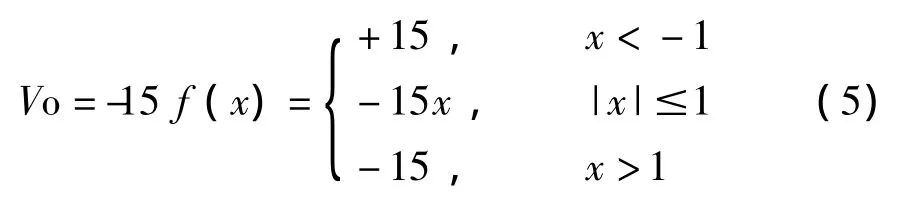
我们完成了限幅电路设计后,可得到了非线性函数的倍数关系,即-15f(x)。下面根据式(2),利用反相比例积分电路、加法电路和反相放大电路等常见的模拟电子电路,对蔡氏电路中三个状态变量之间的代数运算关系进行反推设计。
在图4中,运放U2A和电阻R6、R7构成了反相电路,实现了状态变量y的反相。该输出与图3中限幅电路的输出结果Vo=-15f(x),一起作为运放U3A的输入。它与电阻R4、R5、R8及电容C1构成含加法运算的反相比例积分电路,最终输出为系统状态变量x。

图4 系统变量x引出图
状态变量的引出图如图5所示。运放U4A和电阻R9-R11构成了反相加法电路。其输入为系统状态变量x与z1,输出作为运放U5A的输入,与电阻R12、R13,电容C2构成了含加法运算的反相比例积分电路,最终输出结果即为系统状态变量y。
系统状态变量z与y具有反相比例积分关系,以图5中运算放大器U5A的输出量y作为输入,经过由运算放大器U6A、电阻R14和电容C3构成的反相比例积分电路之后,得到系统状态变量z,电路结构如图6所示。

图5 系统变量y引出图
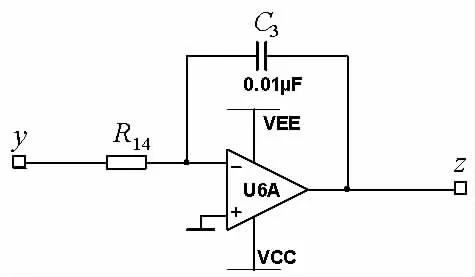
图6 系统变量z引出图
最后,将图4、图5和图6中对应系统状态变量的端口连接,可以得到与蔡氏电路等效的三阶自治混沌电路,如图7所示。图中的等效蔡氏电路的数学表达式为

图7 等效蔡氏电路
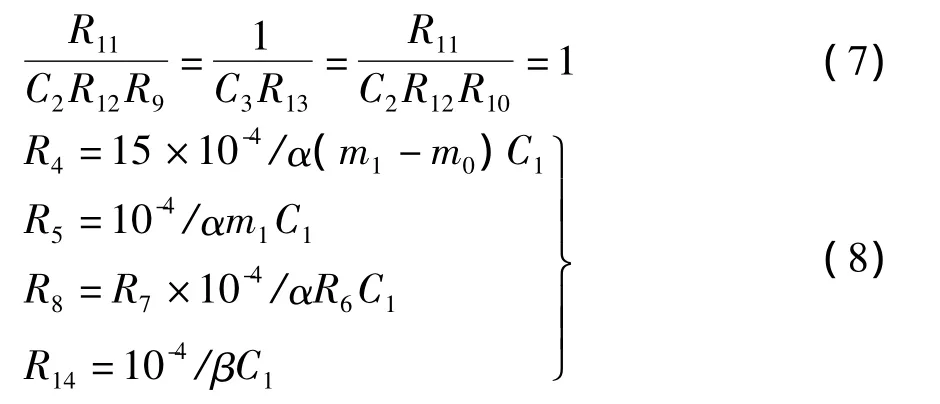
为了方便电路参数取值,将系统所有量整体成比例缩放10倍,缩放后系统的频率加快,系统的运动状态不发生改变。结合式(2)和式(6),可得电路中主要元器件取值依据为

可见,当系统参数m6,m1,α和β发生改变时,随之而发生改变的只有电阻R4,R5,R8和R14。换句话说,这四个电阻参数值的大小直接决定了蔡氏电路系统的运动轨迹。
3 蔡氏电路实验结果
我们按照图7所示的电路图,搭建等效蔡氏电路硬件电路。现设系统的参数m0=-1/7,m1=2/7,β=15,改变参数α,观察其对蔡氏系统运动的变化。为了方便,图4和图5的电路中,选取反相器的电阻R6=R7=R9=R10=R11=10kΩ。同时根据式(7)和式(8)的计算,选取 R12=R13=10kΩ,R14=666.7Ω 和电容 C1=C2=C3=0.01μF。上述电阻选择的误差范围都为1%的精密电阻,三只电容均由允许误差5﹪的103J瓷片电容来实现。我们只需调节3只精密电位器R4,R5和R8的阻值,就可以改变系统参数α的大小,从而观察到不同的系统运动行为。
实验时,利用型号为UTD4062C的示波器观察系统运动的变化情况。当α=9.5时,调节电位器R4=35kΩ,R5=3.5kΩ,R8=1kΩ,观察到此时系统处于双涡卷运动状态,三个系统变量间的相图分别如图8(a)~(c)所示,对应变量x与y时序图如图9(a);当 α =9.0 时调节电位器 R4=38.89kΩ,R5=3.89kΩ及R8=1.11kΩ,此时系统处于单涡卷运动状态,运动轨迹如图8(d)~(f)所示;当α=8.75时,调节电位器 R4=40kΩ,R5=4kΩ 及 R8=1.143kΩ,此时系统处于周期四状态,运动轨迹如图8(g)~(i)所示;当 α =8.5 时,调节电位器 R4=41.18kΩ,R5=4.12kΩ及R8=1.18kΩ,此时系统为周期二状态,三个系统变量间相图如图8(j)~(l)所示;对应变量x与y的时序图如图9(b)所示。当α=7.8时,调节电位器 R4=44.87kΩ,R5=4.49kΩ 及 R8=1.14kΩ,此时系统为单周期状态,三个系统变量之间相图如图8(m)~(o)所示。可见,随着系统参数α减小,蔡氏电路的运行状态经历了双涡卷混沌振荡、单涡卷吸引子、多周期到单周期的演变过程。等效蔡氏电路与经典蔡氏电路图的实验效果图几乎一样。

图8 参数改变时的系统运动轨迹

图9 混沌和周期二运动态的时序对比图
在硬件实验时,系统参数调节很容易,从示波器观察到的波形比较稳定。在以往蔡氏电路实验的相关文献中,只能得到状态变量x与y的相位图,或其时序图,而该实验电路最大的优点是能够从示波器中直接观察到蔡氏系统三个状态变量的运动。即可以观察到状态变量z分别与变量x和y的相位图,及对应的时序波形图。
实验中选择的电阻和电容精度都是比较高,因而实验效果很好,由于蔡氏混沌运动有很强的敏感性,若选择的元器件精度不高,调试电路就比较困难,影响实验效果。
4 结语
本文从蔡氏电路方程出发,逆向推导出与之等效的电路结构图。在运算方式不变的条件下,可以改变电路参量来扩大混沌现象的调节范围,实现方式灵活多样。我们只需要将反相加法电路、反相电路和比例积分电路进行组合连接,就可以实现整个等效蔡氏电路的设计,电路形式简单、可操作性强。此外,因为电路中不含电感元件,系统产生的混沌吸引子相对比较稳定,并且运动轨迹清晰可见,加深了学生对混沌现象本质的认识,给非线性混沌电路的教学带来了极大的方便。
[1]朱雷,包伯成,卜沛霞,乔晓华.蔡氏电路的实验制作[J].南京:电气电子教学学报,2011,33(2).
[2]张新国,徐崇芳,王金双,严纪丛,韩廷武.无电感蔡氏电路设计方法与应用[J].山东:山东大学学报(工学版),2010,40(6).
[3]蒋国平,程艳云.蔡氏混沌非线性电路及其频率特性研究[J].南京:电气电子教学学报,2002,24(5).
[4]龙江涛,姚缨英.蔡氏电路和音频信号保密通信的实验研究[J].南京:电气电子教学学报,2009,31(1).
[5]卢元元,薛丽萍.蔡氏电路的实验研究[J].南京:电气电子教学学报,2003,25(3)

