传输线场、路模型的一致性探讨

颜秋容

(华中科技大学电气与电子工程学院，湖北武汉430074)

均匀传输线作为分布参数电路的代表，是“电路理论”的重要教学内容[1-2]。同时，均匀传输线作为导行电磁波的例子，亦出现在“电磁场”的教材中[3-5]。均匀传输线这个工程应用中广泛遇到的电磁问题，无疑可以采用电磁场理论来建立分析模型(以下称为场模型)。在电磁场理论基础上、加上集中参数假设的电路理论，通过微分元电路，也建立了均匀传输线的分析模型(以下称为路模型)。

我国高校对均匀传输线的教学处理有两种方法:将其放在“电路理论”课程中，或将其放在“电磁场”课程中。一般而言，涉及电力系统电能传输的专业，均匀传输线的教学内容放在“电路理论”课程中，而如通信、电子等与电磁波传播相关的专业，其教学内容放在“电磁场”课程中。

美国的“电路理论”教材中少见均匀传输线内容[6-8]，而“电磁场”教材中一般包含均匀传输线分析内容[2，3]。但是，多数“电磁场”教材在建立均匀传输线分析模型时，还是借用了路的方法。少数教材用场的方法建立均匀传输线分析模型时，仅针对无损耗均匀传输线，因为若考虑导体损耗，基于麦克斯韦方程的模型将过于复杂。

通过场、路方法建立的模型之间如何关联，各自得出的传播特性参数之间的一致性如何，是本文研究的问题。无论是在“电路理论”课程、还是在“电磁场”课程中讲授均匀传输线内容，有利于学生比较深刻理解传输线的传播特性参数、掌握影响传播特性的因素。

1 均匀传输线的场模型

1.1 电磁场的基本方程

线性和各向同性媒质中的电磁场问题，可通过麦克斯韦方程组表达加上如下媒质特性方程和边界衔接条件:

上述方程中:D和E分别为电位移矢量和电场强度矢量;B和H分别为磁感应强度矢量和磁场强度矢量;J为电流密度矢量;v为运流电荷速度矢量;ε、μ、σ、ρ分别为介电常数、磁导率、电导率和电荷密度。

1.2 自由空间中理想导体传输线的方程

自由空间中理想导体构成的均匀传输线如图1所示，也就是电路理论中的无损耗线。

图1 均匀传输线

由于几何尺寸d=l，故x方向的电磁辐射可以忽略。又由于导体和周围媒质均不消耗能量，因此电源提供的能量全部传输到负载，坡印亭矢量为z方向。两线之间的电磁场为E=-Exex，H=-Hyey。结合式(1)、(2)及式(5)、(6)，得到传输线方程为

式中，ε0、μ0分别为自由空间的介电常数、磁导率。由上式得到波动方程为

正弦稳态下，上式变为

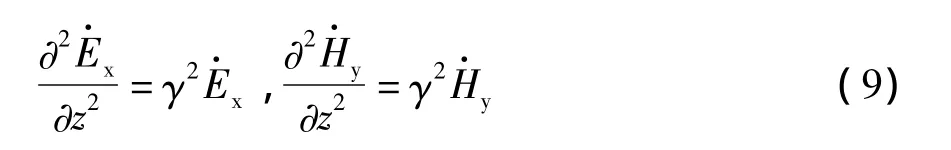
1.3 媒质空间中理想导体传输线的方程

设非理想媒质的电导率为σ，媒质中的传导电流 J=Jxex= σExex，结合式(1)、(2)和式(5)、(6)，得到传输线方程:

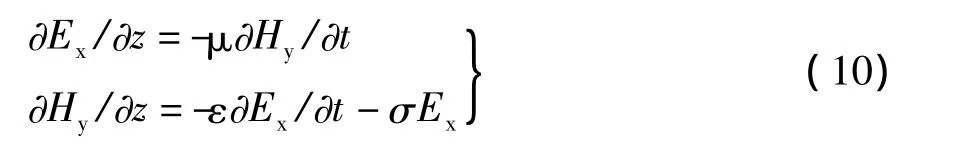
由上式得到波动方程:

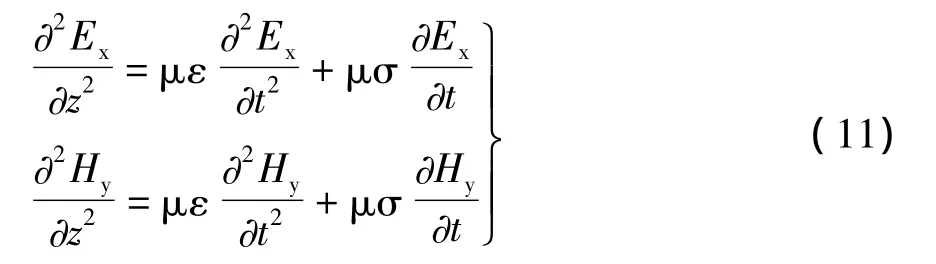
正弦稳态下，上式变为

由此解得

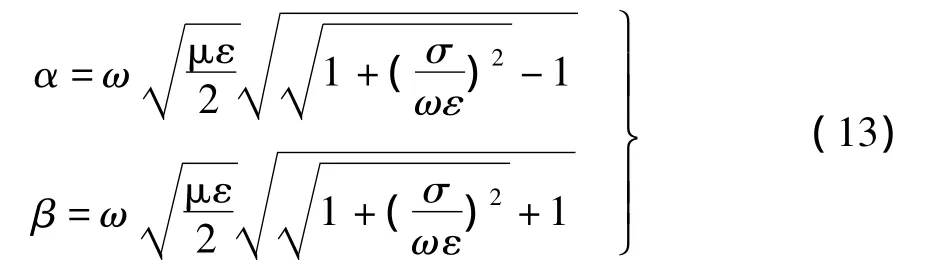
波阻抗为

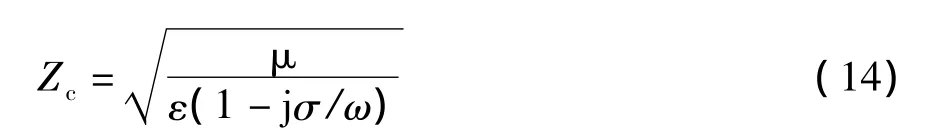
波速为

式(13)～(15)实质上是电磁波在媒质空间中的传播特性参数。当σ=0时，由式(13)～(15)得到:α=0与1.2节中无损耗线的结果相同。

当信号频率高到使σ/ωε=1时，则式(13)～(15)也变成以上结果，本质上是传导电流相对于位移电流可以忽略。

1.4 媒质空间中非理想导体传输线的方程

对于理想导体，电导率σc=∞，电流沿导体表面流动，导体内部电场和磁场均为零。当导体非理想时，电磁能量从导体周围进入导体内部，转换为内部的焦耳热、电场能和磁场能。坡印亭矢量不再仅为z方向分量，两线之间的电场除了x方向分量外，还有z方向分量。因此，不易获得麦克斯韦方程的解，不宜从场的角度来分析。

2 均匀传输线的路模型

在忽略电场z方向分量的前提下(当导体的电导率σ足够大时成立)，两线间媒质中的传导电流、位移电流分别用单位长度电导G、单位长度电容C表示，导体内部的焦耳热用单位长度电阻R表示，导体周围空间和内部的磁场能用单位长度电感L表示，得到图2所示传输线的微分元电路模型。该模型既考虑了媒质的损耗，也考虑了导体本身的损耗。且通过电感L考虑导体内部的磁场储能，L是内自感和外自感的综合，内自感对应于导体内部的磁场，外自感对应于导体外部媒质空间的磁场。

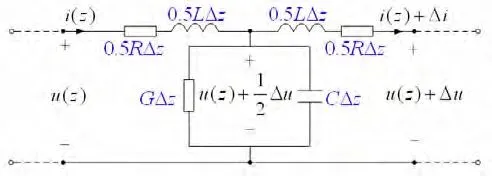
图2 均匀传输线的微分元电路

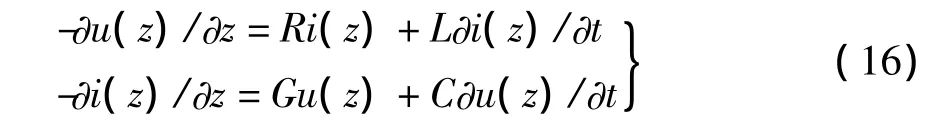
上式即是传输线的路模型。正弦稳态下，由上式获得

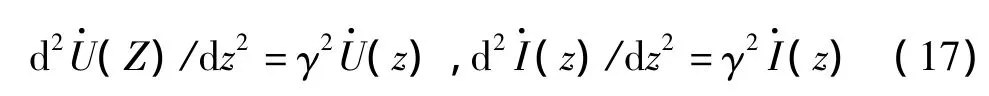
其中，γ =(R+jωL)(G+jωC)= α +jβ 为传播系数，可解得

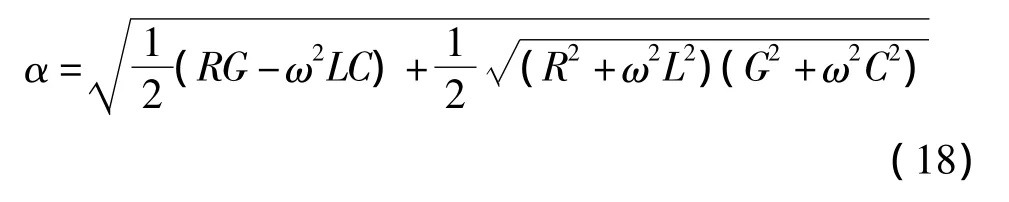
求解式(17)可得波阻抗

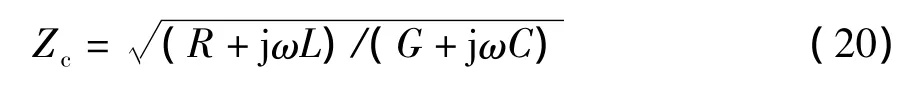
式(18)～(20)是由均匀传输线路模型获得的传播特性参数。

3 场模型和路模型的一致性

本节以平行双传输线为例来探讨场、路模型的一致性。对于导体半径为a、两线中心间距为d的均匀传输线，由电磁场理论求得原始参数如下:

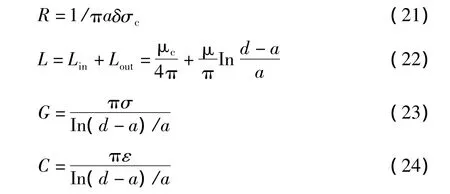
3.1 媒质空间中理想导体传输线模型的一致性

媒质空间中，由理想导体构成的传输线，在路模型中对应于R=0，且由于导体内部没有磁场，内电感为零，即由式(22)得

L=Lout=(μ/π)In(d－a)/a

由此，式(18)～(20)简化为

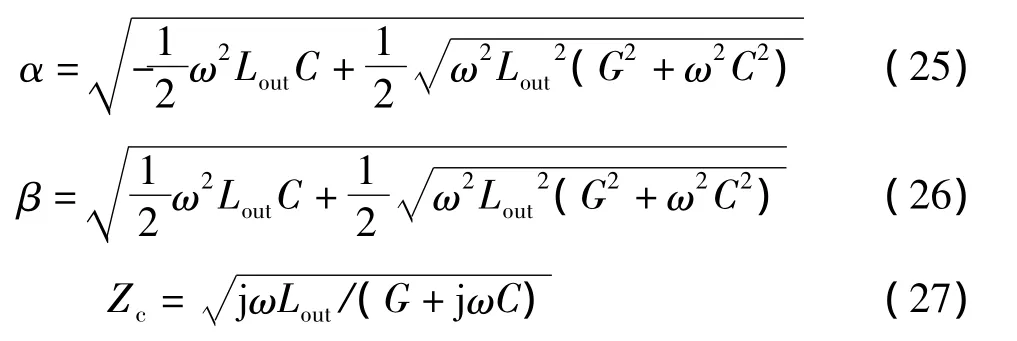
将平行双传输线的原始参数代入式(25)～(27)，便得到式(13)～(14)的 结果。

3.2 自由空间中理想导体传输线模型的一致性

自由空间中理想导体传输线，在路模型中对应于R=0=G，且内自感为零。由此，式(18)～(20)间化为

将平行双传输线的原始参数表达式代入式(29)～(30)，得到这就是无损耗线的传播特性参数，与1.2节的结论一致。

4 传输线、媒质传播特性参数的差异

对场、路模型一致性的分析，有利于深刻理解传输线的传播特性。仅当导体为理想导体时，传输线的传播特性才与周围媒质的传播特性相同。由于不存在理想导体，因此，传输线的传播特性和媒质的传播特性存在差别。例如:

(1)波阻抗:自由空间中电磁波的波阻抗Zc=而据式(14)媒质中，电磁波的波阻抗

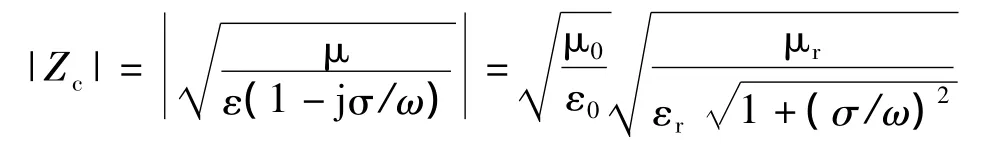
式中，εr，μr为相对介电路常数和磁导数。通常μr≈1、εr＞1，故|Zc|＜377Ω。而对于传输线，由式(20)可知，非理想导体使得传输线的波阻抗模值高于相应媒质中电磁波的波阻抗模值(因为R≠0，L要包含内自感)。因此，架空线的波阻抗模值不一定低于377Ω。

(2)波速:自由空间中电磁波的波速为vp=ω/β)，这也是无损耗传输线的波速。据式(15)，媒质空间中电磁波的波速为

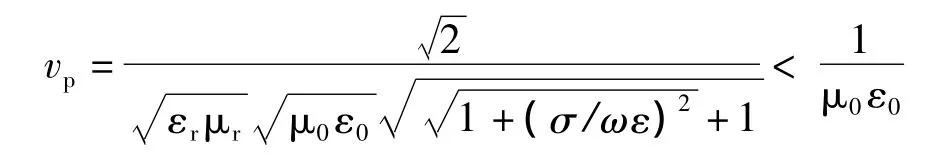
媒质的εr和σ/ωε共同影响波速，这两个值越大，波速比c小得越多。这个结论显然也适用于理想导体构成的传输线。

由式(19)可知，非理想导体传输线的波速还与传输线的电阻和电感相关。为了分析导体的电阻对波速的影响，对式(19)令G=0，即分析自由空间中非理想导体传输线，此时

显然，R越大(L也因此加大)，则β越大，导致vp变小。综上所述，有损耗传输线的vp一定小于无损耗传输线的vp，来源于媒质的损耗以及导体的损耗均降低了传输线的波速。

因此，传输线的波速不仅仅由媒质决定，而是由导体、媒质共同决定。同是架空线，由于导体类型不同，波速也会不同。

5 结语

(1)本文用电磁场理论和电路理论两种方法建立均匀传输线分析模型，论证了两种模型的一致性。

(2)本文从场和路两方面剖析传输线传播特性与其周围媒质传播特性的差异、以及影响传输线传播特性的因素。

(3)本文的分析进一步明确:媒质中电磁波波阻抗的模值不高于377Ω，而传输线波阻抗的模值可以高于377Ω;传输线的波速由导体、媒质共同决定。

(4)本文的研究，有利于从事电路理论和电磁场理论教学的教师加深对传输线传播特性参数的理解。

[1]颜秋容，谭丹主编.电路理论[M].北京:电子工业出版社，2009.

[2]邱关源，罗先觉主编.电路，第四版[M].北京:高等教育出版社，1999.

[3]冯慈璋主编.电磁场，第二版[M].北京:高等教育出版社，1983.

[4]William H.Hayt.Jr.，John A.Buck.Engineering Electromagnetics，Sixth Edition[M].New York:McGraw-Hill Company，2001.

[5]Mathew N.O.sadiku.Elements of Electromagnetics[M].New York:Oxford University Press，2011.

[6]Charles K.Alexander，Matthew N.O.Sadiku.Fundamentals of Electric Circuits[M].北京:清华大学出版社影印，2000.

[7]James W.Nilsson，Susan A.Ricdel.Electric Circuits，Ninth E-dition[M].北京:电子工业出版社影印，2011.

[8]William H.Hayt，Jack E.Kemmerty，Steven M.Durbin.Engineering Circuit Analysis，Sixth Edition[M].New York:McGraw-Hill Company，2002.