基于Fluent的白内障术后房水流体力学数值分析
梁书秀, 郝菲菲, 孙昭晨, 邵 彦, 李亚新
(1.大连理工大学海岸及近海工程国家重点实验室,辽宁 大连 116024;2.大连医科大学附属第二医院,辽宁 大连 116023)
白内障是常见的致盲性眼病,通常表现为眼球内部晶状体内出现混浊.目前尚无治疗白内障的特效药物,一般以手术为主[1].白内障超声乳化手术由于其治疗效果好而成为近年来国内外白内障患者青睐的新型手术.然而仍然存在某些手术并发症是目前尚未克服的.临床医学常见的并发症[2]有后囊膜破裂伴玻璃体脱出、眼压升高、继发性青光眼、后发性白内障和虹膜黏连等.
用数值分析的方法来模拟微观的眼内流体,目前国内尚未有文献查询.自Friedland[3]将房水近似为流体力学模型开始,房水流体动力学逐渐发展.Friedland建立的模型认为眼内所有组织都是刚体并且其位置不受房水流动影响.通过黏性方程的建立和求解得出前后房压力场及速度分布.此后Heys和Barocas的文献[4-5]也通过建立二维弹性模型而得到正常眼球在视觉调节时,即晶状体的曲率变化后的眼压值和前后房压差等数据,还模拟了眼球瞳孔闭锁后引起的虹膜膨隆和眨眼等情况.数值模拟了虹膜在房水作用下的变形,验证了影响眼压值的因素为虹膜和晶体的最小距离以及小梁网的渗透率等.在Heys和Barocas的文献中,通过建立三维模型模拟了自然对流情况下的正常眼球,借助眼内微粒的运动来模拟Krukenberg条纹的形成[6].眼内压力的求解通常用于求解青光眼的问题,本研究创新性地应用求解压力的方法解决白内障术后的问题.
本研究建立三维刚性模型,通过求解黏性方程来解决眼内流体运动,在考虑自然对流情况的前提下,重点研究植入人工晶体后,前后房的压力差变化情况.通过改变虹膜至人工晶体的最小距离,模拟术后虹膜逐渐靠近人工晶体的过程中,眼内压的变化情况,从而探究白内障术后眼内压升降等并发症的产生原因.
1 计算区域模型
房水循环是眼内流体循环的重要组成部分,其在眼内的排出主要有两个途径,即所谓的常规途径和非常规途径.常规途径即房水由睫状体突分泌,经过瞳孔流入了前房,最终通过小梁网流回睫状体前静脉.非常规途径的房水充满玻璃体腔隙,供给玻璃体与视网膜的营养后,入睫状体平部静脉,进入血液循环[7].非常规途径所排出的房水仅占总排出量的约10%[8],因而本研究仅考虑房水在常规途径下的流体运动情况.
由于我们探究的是晶状体周围部分的压力变化情况,主要考虑眼球的前半部分,即眼内晶状体至眼角膜周围的区域.本模型考虑自然对流,在重力的影响下,眼球的模型需要建立三维模型.重力方向为沿着Y轴负方向,且g=9.81 m2/s.将晶状体作为固体研究,假设其为固定不动的刚体,两边的压力相等,所以把晶状体的一半作为模型的一部分研究.本研究模型边界部分分别为眼角膜、晶状体、玻璃体、虹膜、睫状体和小梁网.根据眼睛的尺寸,在虹膜调节瞳孔的过程中,假定虹膜至晶状体的最小距离为2 μm.由于在眼球内部流速很小,并且雷诺数小于2 000,我们将房水的流动近似为层流流动.
图1(1)所示为正常眼球三维模型的二维剖面部分.由于人眼尺寸有差异,取眼角膜的曲率半径为8.3 mm,厚度为 0.5 mm,晶状体到眼角膜的距离为3 mm,并认为此种情况可以代表正常人的眼球尺寸.
进行人工晶体植入术后模型如图1(2),晶状体仅剩晶体囊存在,其为波纹状的层状结构,可以在人工晶体袢的作用下保持原形状并且将人工晶体固定在眼内,前囊厚约为7~11 μm,后壁比前囊薄,约为4 ~7 μm[9].在手术后的模型中,由于人工晶体的直径较正常晶体小,为6 mm,而人工晶体的厚度较正常晶体薄,在这里根据20D人工晶体取其厚度为1.2 mm.手术后在瞳孔调节的过程中和眼内压的作用下,虹膜会逐渐向人工晶体靠拢,根据临床经验,手术一段时间后晶体囊会与人工晶体生长成为一个整体.在术后虹膜向人工晶体靠拢的过程中,通过建立不同间距的模型来计算此过程中前后房眼内压差值.各组织温度和瞳孔大小等其他尺寸均保持不变,也就是只有晶体的直径、厚度和虹膜倾斜角度有了改变,房水的供应速度术后较术前有所增加.此模型模拟白内障术后人工晶体植入到眼球内部,经历足够长时间使其稳定后的情况下,眼内前房和后房压力差的变化情况.
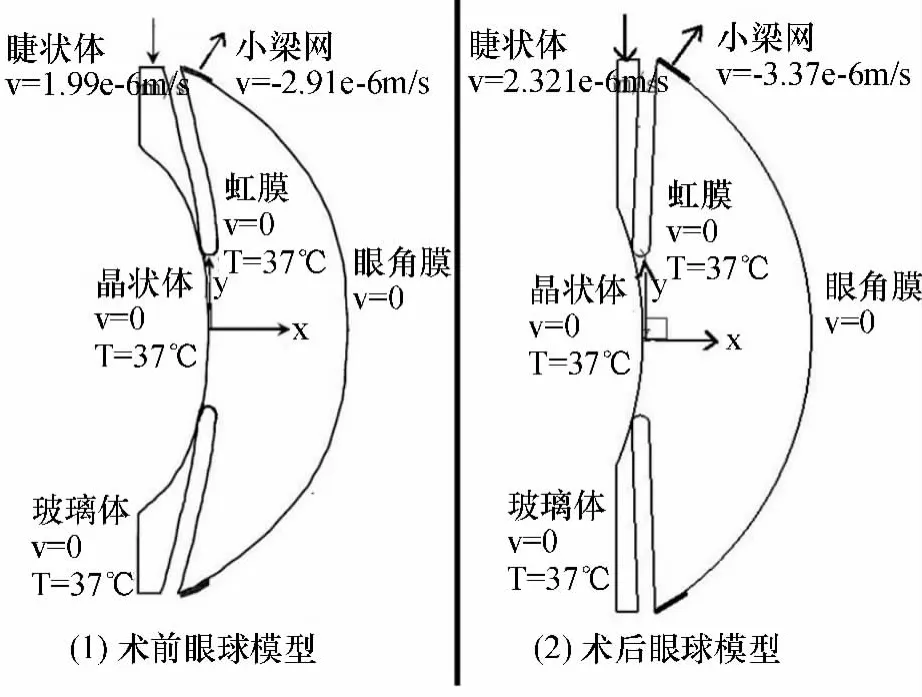
图1 术前和术后眼球模型Z轴剖面图Fig.1 Z-axis profiles of the eyeball before and after surgery models
2 控制方程
在FLUENT中,房水流体动力学控制方程如下:
(1)质量守恒方程
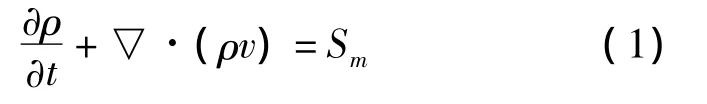
(2)动量守恒方程
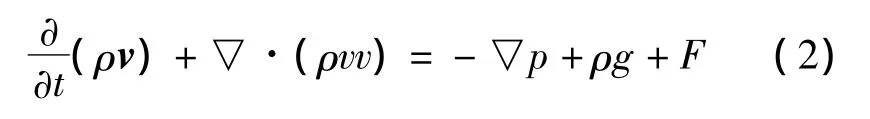
(3)能量守恒方程
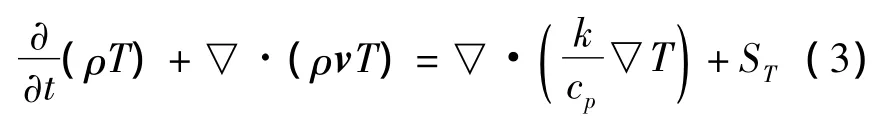
ρ为流体密度,t为时间,v为速度矢量,Sm为质量源项,p为静压,ρg和F分别为重力和外力项,T为温度,k为传热系数,cp为比热容,ST为黏性耗散项.
在混合对流中,浮力的影响可通过格拉晓夫数Gr与雷诺数Re之比来判别:当此数值接近或超过1.0时,浮力对流动将有较大影响.本模型的值大于1.0,故要考虑自然对流.在纯粹自然对流中,浮力引致的流动强度可由瑞利数Ra判定:
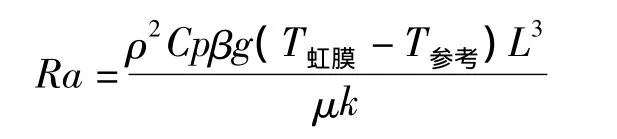
在本模型中,浮力驱动的对流为层流.从自然对流的机理考虑,流体的运动是由于浮力引起的,因而惯性力和浮力有相同的量级.在流体温差较小的情况下,房水采用Boussinesq近似是正确的,温度对密度的影响没有在能量方程中而是在动量方程中体现.此模型的自然对流层流假定是合理的.
则控制方程的简化形式为:
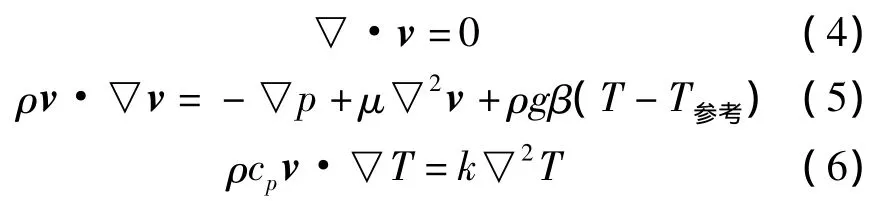
为了更加明确各个物理量对结果变化的影响,减少由于方程中数量级不同引起的差异,对方程进行无因次化如下:
则方程的无因次形式为:
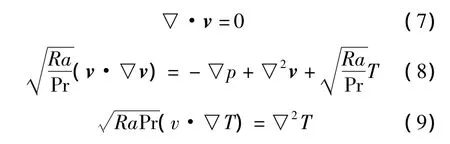
其中式(8)中v有3个方向的速度分别为u、v、w,共5 个方程,5 个未知量,分别为 u、v、w、p、T.对于本模型,采用Boussinesq近似即 ρ=ρ0[1-β(TT参考)].μ 为动力黏性系数,g为重力加速度,T参考为参考温度取34℃,表1给出详细的参数取值.

表1 模型选用的物理参数值Table1 Physical parameters used in the model
3 边界条件的设定
3.1 入口边界条件
人体平均动脉压和眼压分别为(75.49±1.26)mmHg 和(16.22 ±0.50)mmHg[11],由于脉络膜的血流速度在人体所有组织中是最高的,有大约85%的眼部血液都流经脉络膜[12],房水的生成速率不受眼内压的影响,这样便保证了房水入口流量供给.在正常眼球的模型中,房水流量为2.4 μL/min.入口处为睫状体,此处将睫状体设定为速度入口,温度为体温37℃,根据模型尺寸的设定,简化入口的速度都为 v=1.990 μm/s.而在术后模型中,根据术前和术后模型的体积比,从而计算出术后模型的房水流量为2.8 μL/min,根据入口面积计算入口流速 v=2.321 μm/s.
3.2 出口边界条件
出口为小梁网组织,将此出口设定为速度出口,从而保证了前后房房水的体积不发生变化.温度为37 ℃,术前模型的速度 v=-2.910 μm/s,术后模型的速度 v=-3.370 μm/s.负号代表流动方向为流出模型,速度的方向设定为垂直于出口的边界面.
3.3 眼角膜边界条件
眼角膜是内部无血管的透明组织,其传热性质和水相近.由于眼角膜是暴露在空气当中的,在蒸发与辐射的影响下,其温度低于体温,将眼角膜设定为固定的无弹性无滑移边界,速度的边界条件为0,根据文献[13]的测量值,近似取其热导系数为房水的热导系数0.58.忽略了眼角膜的蒸发因素导致的辐射影响,眼角膜的温度设定为固定值34℃,其厚度设定为 0.5 mm[14].
3.4 壁面条件
将玻璃体和晶状体视为固定无滑移边界条件,没有热通量和质量通量通过,晶体纤维平行前囊整齐排列,这种结构使晶体在因调解而引起变形时,不致因变形运动而滑脱,我们将此结构也视为壁面条件.由于毛细血管内部血液的循环作用,眼球内部的温度保持为恒定值即体温37℃.根据Tiedeman的模型假定,本研究忽略了虹膜内部液体的流动及其对位置的影响[15].
3.5 求解软件与计算过程
Fluent软件对流体流动与传热模型的自然对流模拟计算流程为:将mesh生成的网格模型导入Fluent进行边界条件的设置,利用Fluent 3D单精度求解器对流动区域进行求解计算,欠松弛因子和离散格式均采用默认值,模型选用耦合式求解法.为保证计算精度,采用有限体积法对计算模型区域作离散化处理.由于Re<2000,因而流动为层流.动量和能量方程离散采用二阶迎风格式[16],压力和速度采用SIMPLE算法.将虹膜的侧面进行了细致的网格划分.图2中分别为眼球侧向的视角和晶体方向的视角及局部网格放大图示.离散后的方程组运用了fluent软件进行求解,化分了精密的四面体非结构三维网格,术前的正常眼球划分1 608 591个四面体单元,术后模型划分了644 445个单元.软件选用了有限体积法,层流模型,耦合求解法进行稳态求解.
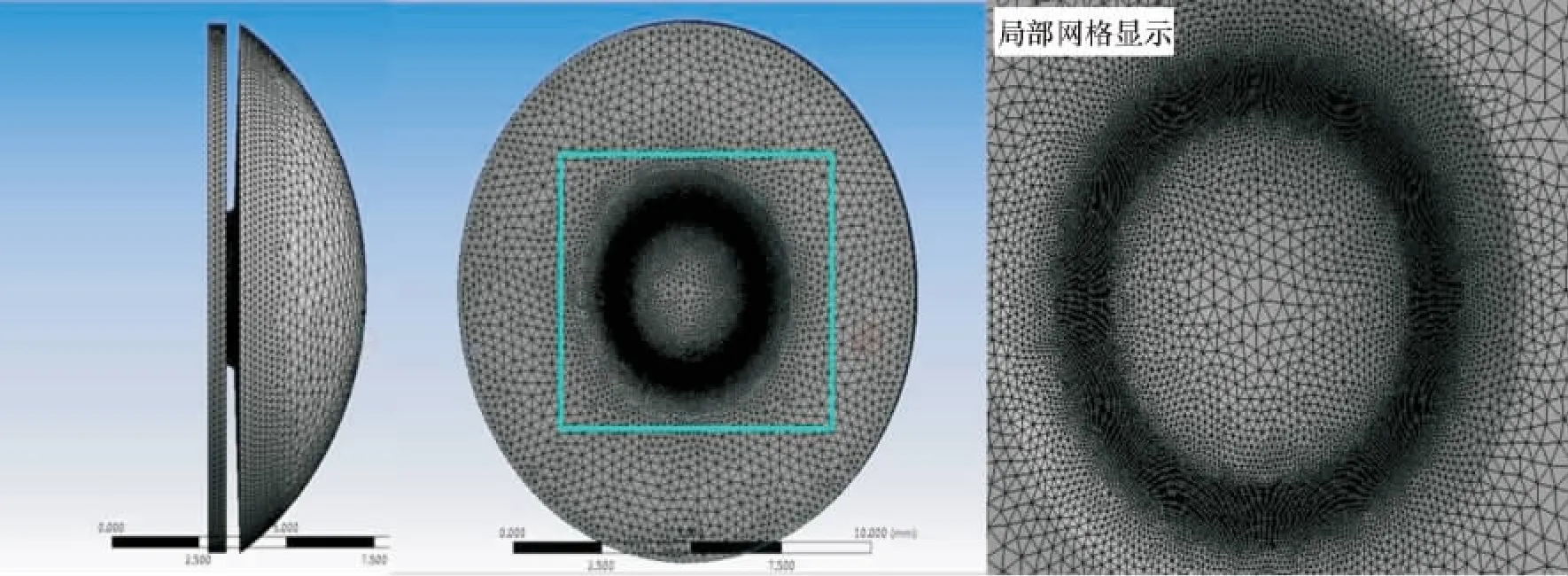
图2 模型网格的显示Fig.2 The demonstration of the model grid
4 结果与讨论
在本模型中,计算了正常眼球模型的压力场、速度场和温度场.其温度场和流场的分布图与Heys和Barocas文献中的一致,证明本模型参数选取的合理性.图3为计算结果.
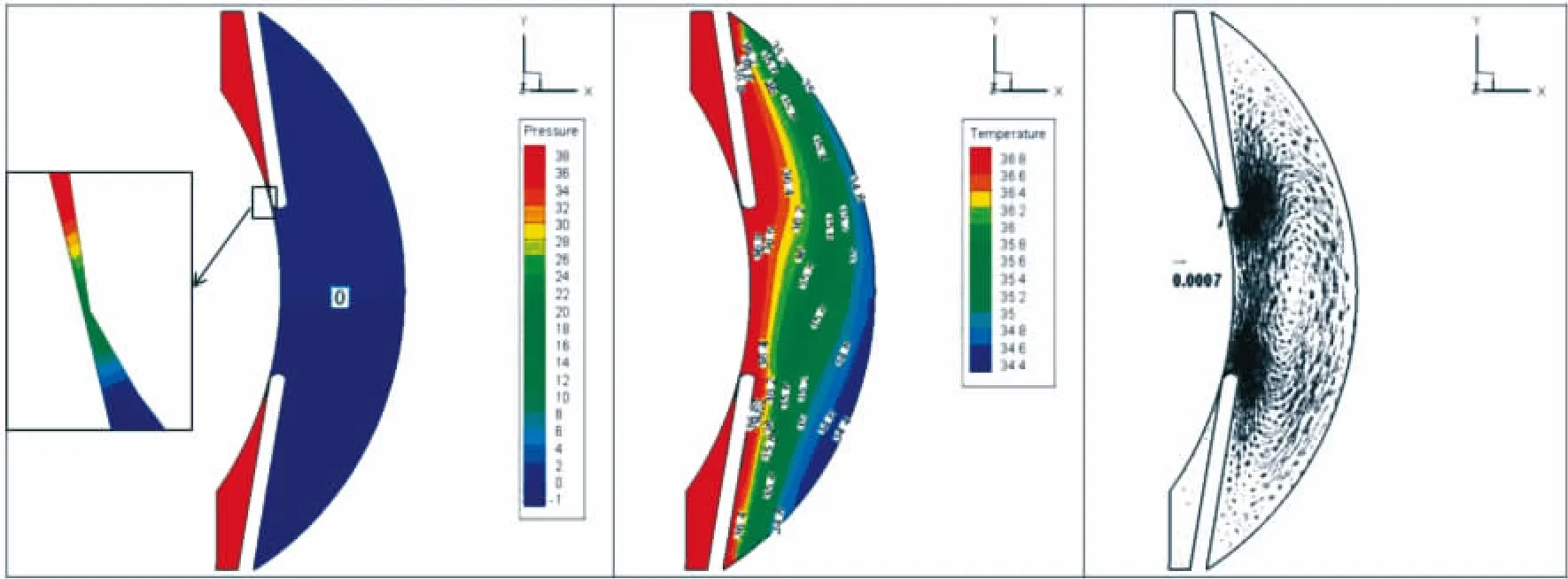
图3 正常眼球的压力场、温度场和流场Fig.3 The pressure,temperature and flow field of nomal eye
4.1 正常眼球情况(此工况为虹膜至晶体的最小距离为2 μm情况)
在正常眼球模型中,通过结果分析和表2对比,晶体和虹膜的最小距离为10 μm时,与2 μm情况下比较,眼球的前后房的压力差将减小,而最大速度不会有很大的变化,此最大流速出现在前房靠近边缘处(如图4).说明此速度是惯性力与由温差产生的浮力共同作用的结果.将眼角膜的温度设定为37℃,也就是在没有温度差存在的情况下,不存在自然对流的影响,速度场和压力差完全是由进口的流体产生的,这时候前后房的压力差基本没有改变.只要前后房有温差,就会形成自然对流.虹膜至人工晶体的最小距离对前后房的压力差大小影响明显.在压力场中,最小压力出现在前房下部区域,但是前房的压力场整体相差不大,只有前房和后房的相对压力有明显差值.由图4中可以看到,速度的云图出现了两个峰值区域,这与文献[4-5]中的速度矢量图分布一致.速度的峰值区产生了动压的相对峰值区域,其分布与速度云图相似.在最小间隙为2 μm的情况下,动压最大处仅为0.002 1 Pa,与静压相比不在一个量级,压力场的计算为动压加静压,前房动压的差异不会引起总压力场的分布形态.
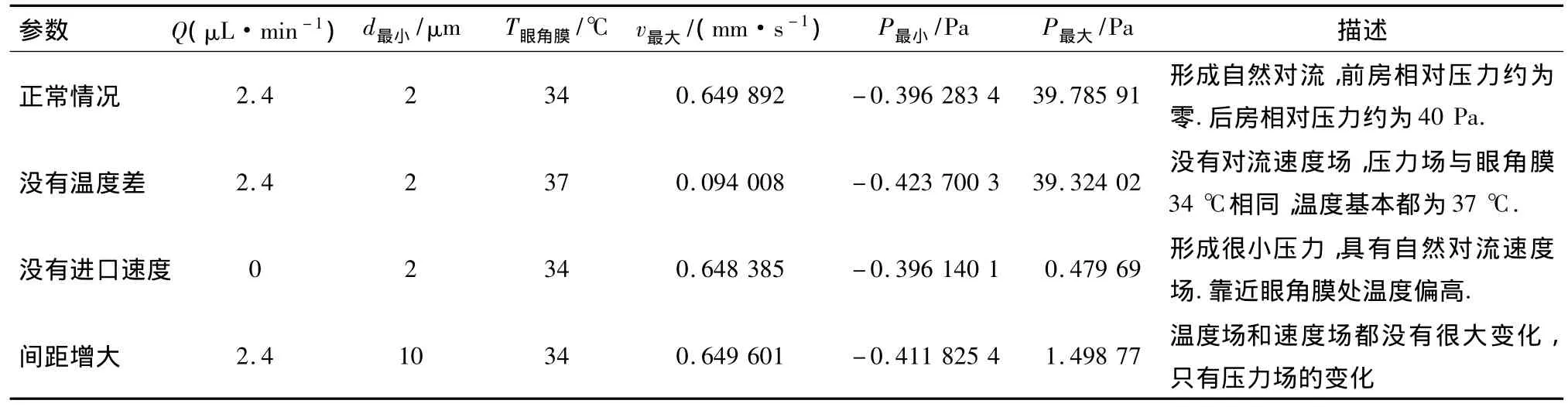
表2 正常眼球前后房压差影响因素Table2 Influencing factors of pressure difference between chambers of normal eye
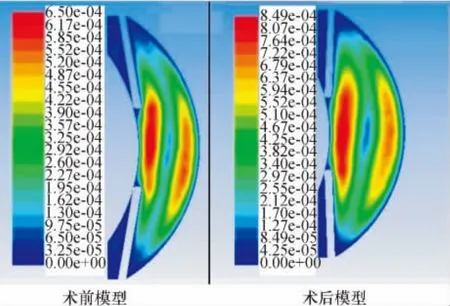
图4 术前和术后模型速度云图Fig.4 Contours of velocity magnitude of the models before and after surgery
房水在眼球内部靠近晶状体和虹膜温度较高的位置,密度比较小,而在靠近眼角膜的位置由于温度比较低,密度较大,密度的差异变化产生了垂向的浮力.密度大温度低流体会向下流动,密度小温度高的流体有向上流动的趋势,这样在浮力的驱动下,就形成了自然对流,二维切面中是一个顺时针方向的流动.由等温图可以看到,在贴近壁面的区域,等温线与壁面平行,这与壁面是恒温的前提是一致的,而重力的原因使其非对称.从速度矢量图和等压差值线图(图3)中可以看到,在前房靠近眼角膜的地方对流强烈,在区域的中间有一个总压的低压区,此处的流速较小.入口速度的大小对压力差影响比较大,温度差对对流的强弱有影响.研究发现0.02℃的温度差就可以形成自然对流[17].
在眼科临床中由炎症引发的角膜后沉着物(KP)尤为常见,其量多时外形为不规则且反光的羊脂状物[18].当虹膜、睫状体等位置出现炎症时,内皮细胞肿胀,发生有形物质的沉着形成KP.根据本研究,前房靠近角膜处温度较低,且温度场出现不均匀分布即上高下低的趋势,加之重力的影响,使组成KP的有形物质形成山峰形沉着于角膜中下部.当细胞量过多时,房水的对流带动KP在前房内部的循环,使其不仅在角膜后壁,且可在房水内浮动,同时也沉积于晶体表面呈现所谓晶体沉着物,细胞和纤维素过多时可造成前房角粘连,虹膜晶体粘连,进而导致继发性青光眼和白内障[19].
4.2 术后眼球(图5均是虹膜至人工晶体距离为2 μm情况)
在本模型中的压力均为相对压力值,压力零点选为坐标零点,即为晶体的中心点处.图5为术后虹膜向靠近人工晶体靠近过程中模型内最大压力、最大速度和最小压力的变化.
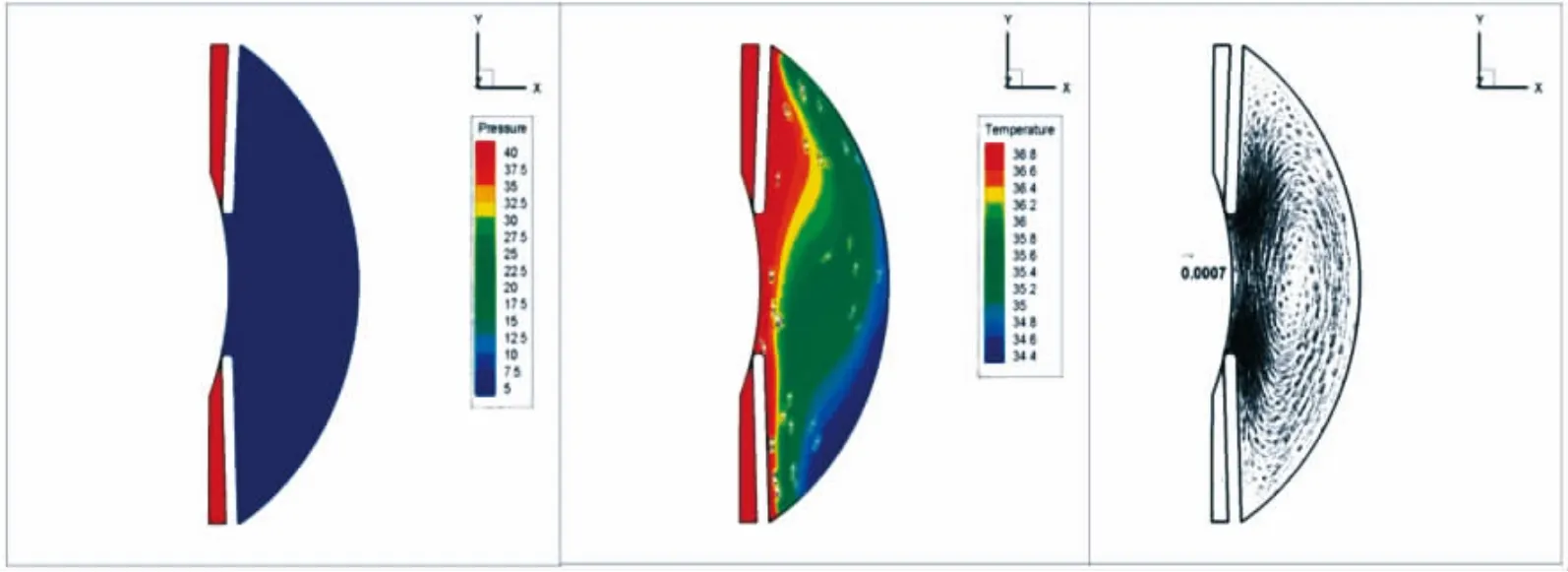
图5 术后眼球内的压力场、温度场和流场Fig.5 Pressure,tempreture and flow field of the eyeball after surgery
通过图6、表3的比对可得出,在人工晶体植入后,前房和后房的压力差将有所增大.而靠近人工晶状体的位置处眼内房水的流速将有增长的趋势,从而推动虹膜向人工晶状体靠拢.本研究分别模拟了虹膜到晶体的距离为 10、8、6、4、2 μm 的情况下眼压值的变化,即在术后虹膜逐渐靠近人工晶体的过程前后房眼压差值变化.虹膜瞳孔缘前临前房轴部,后临虹膜晶体间隙,前者流场截面积远大于后者,Q=v·A,流量不变,前者的速度远小于后者,根据伯努利方程:,虹膜前部的房水压力显然大于后部,使瞳孔边缘受到了由前向后的推动压力.这种压力与瞳孔的大小无关,而是与虹膜与晶体间隙最窄处的流场截面积有关.瞳孔中度散大时,瞳孔缘几乎与晶状体前凸面相接触,产生最窄间隙,易于发生瞳孔阻滞[20].并且在术后的模型中,增大的流速会加快前房局部房水的循环,也可能会引起KP的运动加强,发生KP的流出而阻塞小梁网等情况.
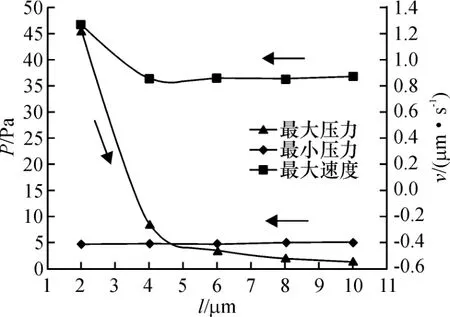
图6 眼内压力差、速度与虹膜和晶体的最小距离的关系Fig.6 The relationship between Intraocular pressure difference,velocity and the gap between iris and pupil
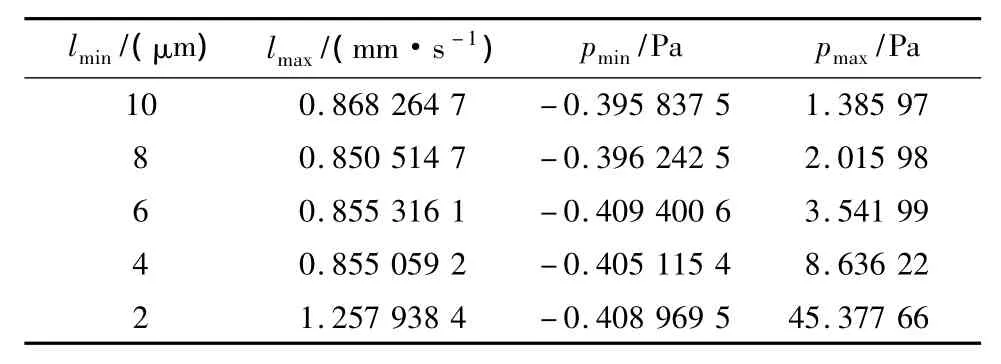
表3 术后眼球前后房压差与虹膜和晶体的最小距离关系Table3 The relationship between intraocular pressure drop between chambers and the gap between iris and pupil of eyeball after surgery
4.3 术后人眼平卧状态时的情况(此时重力的方向为X轴负向)
为了探究在术后人体的姿势对术后眼睛恢复的影响,模拟在手术后人体平卧状态,眼内压和温度场等的变化.本研究通过建立数学模型描述了在人体平卧时,也就是重力的方向为X轴的负向,此时眼内压差的变化情况.从图7中可以看到,在将重力的方向改为X轴负向时,温度场的形状成为了完全对称,流场形成了一个双向的循环,但眼内压差的变化不明显,说明重力的影响不会对眼内压差产生很大的影响,眼内压增减的并发症不是重力的方向变化引起的.
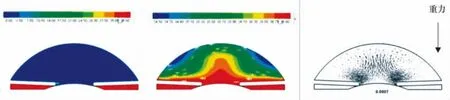
图7 人体平卧时术后压力场、温度场和流场Fig.7 Pressure,temperature and flow field of supine eyeball after sugery
5 结论与展望
由以上数据可以得出,在人工晶体植入眼球后,眼球的前后房压力差有了增大的趋势,并且虹膜越靠近人工晶体,压力差的增长越快.眼球内部存在自然对流且二维切面中是一个顺时针方向的流动.重力的作用使等温图非对称.在前房靠近眼角膜的地方对流强烈.睫状体产生房水流量的大小对压力差影响较大,温度差对对流的强弱有影响.根据白内障手术的临床经验,一定要控制好眼压,尽力避免玻璃体脱出等症状.瞳孔中度散大时,瞳孔缘几乎与晶状体前凸面相接触,产生最窄间隙,虹膜瞳孔缘前临前房轴部,后临虹膜晶体间隙,前者截面面积远大于后者,根据伯努利方程,其前方的房水压力大于后者,使得瞳孔缘部受到从前向后的压力,从而产生瞳孔阻滞的趋势.因此,白内障手术临床中将瞳孔散大[21]扩大虹膜至晶体的距离,不仅方便手术的进行,而且可以防止局部眼压过大,从而降低前后房的压力差,预防虹膜粘连和瞳孔阻滞.
由于在本模型中,虹膜认为是刚性且固定不动的,而实际情况中,虹膜是弹性体,其刚度约为27 kPa[4].增大的前后房压力差,对于弹性体会导致很大的变形,从而导致虹膜至晶体的间距减小导致其压差的继续增大,或者引起虹膜粘连和虹膜膨隆,前房变浅或是房角变窄,导致房水流出受阻,继而引起眼压的升高等症状.从而可以得出,将虹膜作为弹性体研究是必要的,此部分工作需要继续研究.目前眼科医学界对房水的生理和病理机制尚不明确,希望通过房水流体动力学对眼科学的理论发展有所推动.
[1] 周国英.白内障超声乳化和现代囊外摘除术的临床对比研究[C].第十届全国中西医结合眼科学术会议暨第五届海峡眼科学术交流会论文汇编,2011.
[2] 廖 武,曾广川,詹卫群,等.白内障超声乳化吸除与囊外摘除人工晶体植入术后前房角对比观察[J].眼科学报,2000,16(2):99-101.
[3] FRIEDLAND A B.A hydrodynamic model of aqueous flow in the posterior chamber of the eye[J].Bulletin of Mathematical Biology,1978,40:223-235.
[4] HEYS J J,BAROCAS V H,TARAVELLA M J.Modeling passive mechanical interaction between aqueous humor and iris[J].Journal of Biomechanical Engineering,2001,123:540-547.
[5] HEYS J J,BAROCAS V H.Computational evaluation of the role of accommodation in pigmentary glaucoma[J].Investigative Ophthalmology & Visual Science,2002,43:700-708.
[6] HEYS J J,BAROCAS V H.A boussinesq model of natural convection in the human eye and the formation of krukenberg's spindle[J].Annals of Biomedical Engineering,2002,30:392-401.
[7] 田 华,刘九云,田克嶺,等.关于房水循环途径的讨论——两路房水循环说[J].美中国际眼科杂志,2001,1(3):88-90.
[8] BECKER B,NEUFELD A H.Pressure dependence of uveoscleral outflow[J].J Glaucoma,2002,11:464-481.
[9] 张惠蓉,吴慈群.正常晶体和实验性白内障扫描电镜观察[J].实用眼科杂志,1992,10(6):334-336.
[10] BESWICK J A,MCCULLOCH C.Effect of hyaluronidase on the viscosity of the aqueous humor[J].Br.J.Ophthamol,1956,40(9):545-548.
[11] KIEL J W,VAN HEUVEN W A J.Ocular perfusion pressure and choroidal blood flow in the rabbit[J].Experimental Eye Research,1995,60:267-278.
[12] BILL A.Blood circulation and fluid dynamics in the eye[J].Physiological Reviews,1975,55(3):383-417.
[13] SCOTT J A.A finite element model of heat transport in the human eye[J].Phys Med Biol,1988,33:227-241.
[14] KOBAYASHI A S,WOO S L Y,LAWRENCE C,et al.Schlegel.Analysis of the corneo-scleral shell by the method of direct stiffness[J].Journal of biomechanics,1971,4(5):323-326.
[15] TIEDEMAN J S.A physical analysis of the factors that determine the contour of the iris[J].American journal of ophthalmology,1991,111:338-343.
[16] 王福军.计算流体动力学分析——CFD软件原理与应用[M].北京:清华大学出版社,2004.
[17] KUMAR S,ACHARYA S,BEUERMAN R,et al.Numerical solution of ocular fluid dynamics in a rabbit eye:parametric effects[J].Annals of Biomedical Engineering,2006,34:530-544.
[18] PILLAI C T,DUA H S,AZURRA-BLANCO A,et al.E-valuation of corneal endothelium and keratic precipitates by specular microscopy in anterior uveitis[J].Br J Ophthalmol,2000,84:1367-1371.
[19] 叶丽南.KP 的临床意义[J].实用眼科杂志,1984,2(3):132-133.
[20] 王维亿.房水流体力学探讨[R].医用生物力学,1994,3(9):172-176.
[21] 侯利环,黄海玲,钱玉秀.白内障超声乳化与人工晶体植入术的手术配合体会[J].暨南大学学报:自然科学与医学版,2001,2:66-70.

