POLYFLOW在聚合物熔体压力流动教学中的应用

徐 斌，李光明

(西南科技大学，四川绵阳 621010)

聚合物流变学是重要的专业基础课程，聚合物流变测量理论，特别是毛细管口模中的聚合物流动，无论在理论研究还是在高校教学中都占有重要的地位。聚合物在毛细管口模流动过程中，涉及熔体的速度分布、压力分布以及粘性耗散现象，许多重要的规律都是建立在这些现象上的。在聚合物流变学教学中需要采用现代化的教学手段为学生提供观察物理现象的机会，提高学生学习兴趣，培养学生思维水平和创新能力。

聚合物流变实验需要稳定的环境和精密的仪器，而这有时会使实验变得困难。如果能将计算机模拟软件Polyflow引入聚合物流变学教学，利用其可视化功能对流动过程和实验现象比如粘性耗散引起的温度场变化进行计算机模拟，能在没有实验仪器的协助下完成精确地计算与显示，再现聚合物熔体的流动过程和粘性耗散现象，提高学生的学习效率与学习积极性。

随着计算机技术的发展，计算机模拟在现代教学研究中发挥越来越重要的作用［1］。Polyflow软件在聚合物加工成型领域有着许多应用［2］。将Polyflow强大的数值仿真与图形后处理功能的结合将解决许多现实问题，所以Polyflow的计算与仿真应用到教学中有着非常重要的意义。

1 聚合物流变实验及模型系数

本文的设计思路是通过双料筒毛细管流变仪获取聚合物熔体粘度数据，通过数据拟合得到流变模型。然后通过Polyflow软件设置材料参数进行计算实现模拟仿真，再调用计算结果文件，以期达到直观显示的效果。另外通过仿真压力值和实验测量结果对比，加深学生的理解。

实验仪器选用Rosand-RH7双料筒高分辨率毛细管流变仪，材料为盘锦石化公司生产的5070型高密度聚乙烯(HDPE)，熔体温度为220℃。

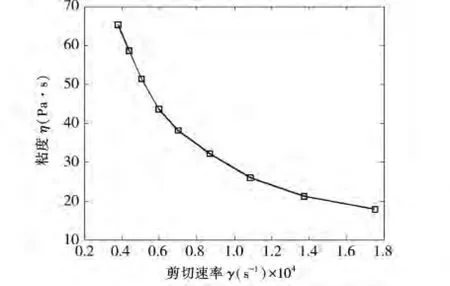
图1 HDPE粘度与剪切速率关系曲线

粘度模型采用式(1)，

式中:K为稠度，˙γ为剪切速率，n为非牛顿指数，A1、A2、T*为模型参数，T为熔体温度。通过数据拟合得到粘度模型系数见表1。

表1 粘度模型系数

由差示显示量热仪(DSC822)测得HDPE材料的玻璃化转变温度分别为136℃。即T*为393．15 K。采用不同温度的粘度数据通过计算得A2为51．6，A1为2．0。由相关资料［5］查得HDPE材料的比定压热容(cp)、导热系数(k)、密度(ρ)，其结果见表2。

表2 材料参数

2 数值模拟

选取圆形截面的通道，直径为1 mm，长径比为16，几何模型见图2;在gambit软件中划分网格，网格单元采用三角混合网格，分布见图3。

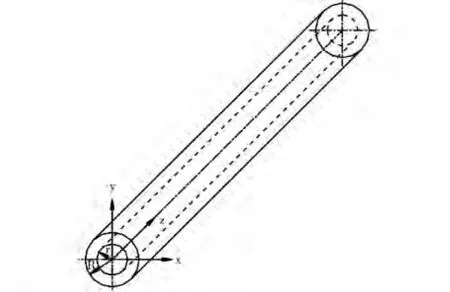
图2 通道几何模型

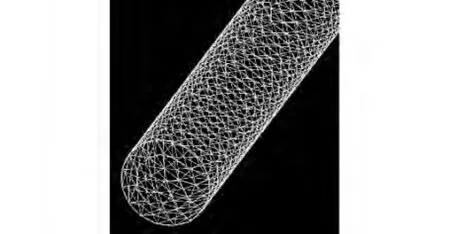
图3 通道网格分布图

3 结果讨论

对表观剪切速率为8 500 s－1为例进行数值计算。设置熔体入口温度为220℃，熔体不可压缩。

其径向速度分布如图4所示，径向速度分布矢量表示如图5所示。剪切速率如图6所示。剪切粘度分布如图7所示。压力沿管长方向分布如图8所示。绝热边界条件下的温度分布如图9。

聚合物熔体在圆管中流动时，根据流变学方程得到径向速度分布方程为

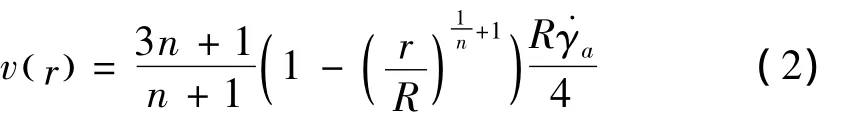
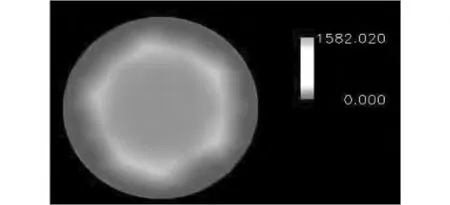
图4 圆管截面速度分布

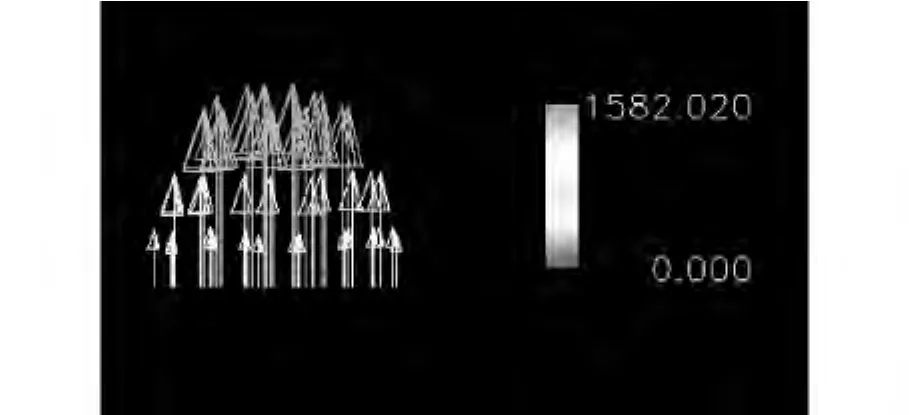
图5 圆管截面速度矢量分布

对于剪切速率，可以根据公式(2)得到

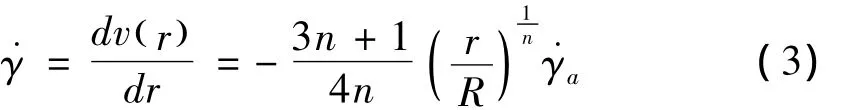
当r=0时，剪切速率为 γ˙=14 548．07，与数值计算结果较符合。从图6中可以看出，剪切速在管壁处达到最大，在管中心部位最小，与理论预测比较相符。

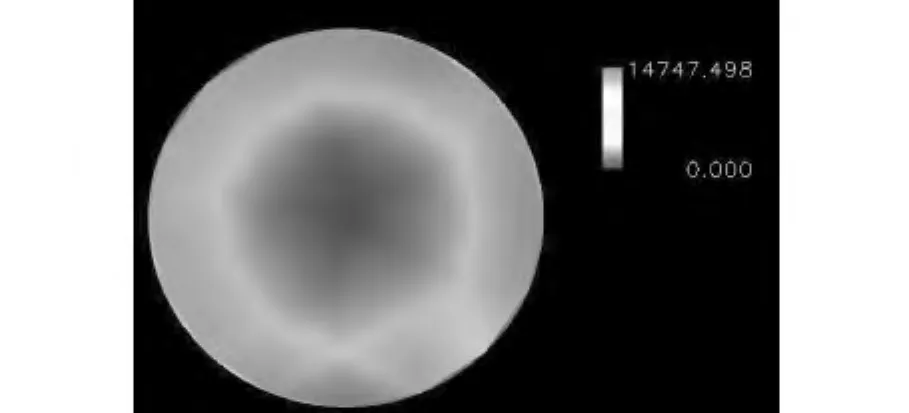
图6 剪切速率分布

对于剪切粘度，可以根据式(1)计算得到管壁处剪切粘度为17．2 Pa·s，与数值计算结果较接近。从图7中可以看出聚合物熔体的粘度随着半径的增大而逐渐减小，这是由于管壁处剪切速率最大，剪切粘度最小。

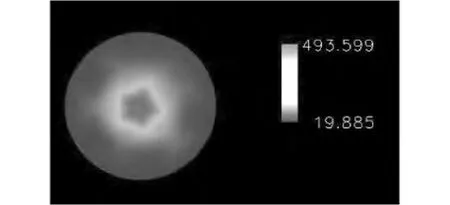
图7 剪切粘度分布

从图8可以看出，聚合物熔体在入口处压力最大，由于熔体不可压缩，在出口部位为零。实验测量结果为16．45 Mpa，与图8中数值模拟接近。

图8 沿管长方向压力分布

当聚合物熔体在圆管中流动时，会因粘性剪切摩擦产生热，导致熔体沿径向温度沿半径发生变化。由于管壁处剪切速率较高，剪切摩擦摩擦较强，因而温度较高，而管中心部位剪切速率小，温度较低，图9中模拟结果相一致。

在这些演示中，学生可以清楚地看到聚合物熔体在圆管中流动时的速度、压力、粘度、剪切速率和温度分布，并可以将不同剪切速率下的计算结果进行比较，便于学生加深理解。

图9 绝热边界条件温度分布

4 结束语

本文通过使用Polyflow软件通过模拟计算聚合物熔体在圆管中流动分析过程，得到各个物理场量的分布图片。可以看出，利用Polyflow软件能够实现聚合物流动过程分析辅助教学，可以在培养学生的学习兴趣，加深学生对于相关知识的理解，培养学生独立思考的能力等方面起到积极的作用。

［1］ 王奎龙．基于Labview的光学现象模拟［J］．大学物理实验，2013，26(6)．

［2］ 韦小雄，王学生，林珩．Polyflow软件在聚合物成型中的应用进展［J］．上海塑料，2008，(4):1-5．

［3］ 钱欣，许王定，金杨福．POLYFLOW基础及其在塑料加工中的应用［M］．化学工业出版社，2010．

［4］ 史铁钧，吴德峰．高分子流变学基础，化学工业出版社，2009．

［5］ 徐佩弦．高聚物流变学及其应用［M］．北京:化学工业出版社，2003．