“几何画板”在李萨如图形中的应用
王明美
(合肥师范学院,安徽合肥 230601)
当一个质点同时在X轴和Y轴上作简谐运动,形成的图形就是李萨如图形。
李萨如图上的每一个点都可以用以下的公式进行表示:
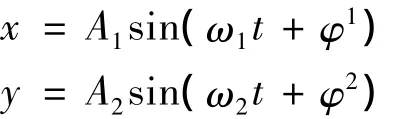
从这里可以看出,李萨如图实际上是一个质点同时在X轴和Y轴上作简谐运动形成的。但是,如果这两个相互垂直的振动的频率为任意值,那么它们的合成运动就会比较复杂,而且轨迹是不稳定的。然而,如果两个振动的频率成简单的整数比,这样就能合成一个稳定、封闭的曲线图形,这就是李萨如图形。[1-2]
几何画板是一款优秀的很适合数学、物理教学和学习的教育软件平台。其特点是简单实用,不需要编程,学习容易,操作简单,交互性强。[3]用几何画板可以轻松实现描绘李萨如图形,并且能够描绘出的动态图形。文献3中介绍了使用旋转矢量的方法[3],本文介绍用谐振动方程合成的方法,分别对于两个相互垂直的同频率的谐振动的合成和两个相互垂直的频率成整数比的谐振动的合成绘制动态图形。
1 两个相互垂直的同频率的谐振动的合成
设有两个相互垂直的同频率的谐振动,其振动表达式分别为
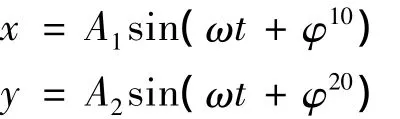
式中:ω 为两个振动的角频率,A1、A2和 φ10、φ20分别为两振动的振幅和初相位。把参量t消去,就得到轨道的直角坐标方程
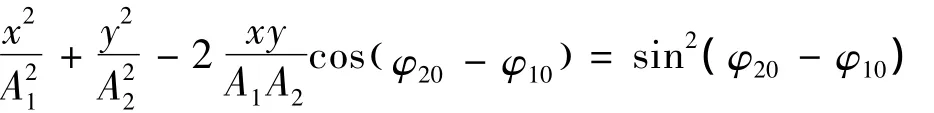
一般地说,上述方程是椭圆方程。特别地,当φ20-φ10=0,π时,质点的轨迹是一条直线。
以下是几何画板5.05的具体步骤。
(1)新建一个画板文件,保存文件名为李萨如图形.gsp。
(2)建立坐标系、设置参数
1.1 建立坐标系
使用“绘图”的“定义坐标系”,建立直角坐标系Oxy。使用直线工具建立平行于x轴线段AB,注意将A点设置在y轴上,设置为t轴。
1.2 设置参数
在AB线段即t轴上用点工具制作点C,选中C,使用菜单“度量”中的“横坐标”,将标注中“xC”改为“t”。使用菜单“数据”中的“新建参数”,设置x轴谐振动振幅A1=1厘米,y轴谐振动振幅A2=2厘米,x轴谐振动初相位a1=0°,y轴谐振动初相位a2=45°。
2 计算t时的自变量值和函数值
使用菜单“数据”中的“计算”,输入A1*cos(w1*t+a1)算出x值,同理输入A2*cos(w2*t+a2)算出y值。
3 设置轨迹和动画
依次选中x值和y值,使用菜单“绘图”中的“绘制点(x,y)”,制作出点 D,依次选中 D、C点,使用菜单“构造”中的“轨迹”。
依次选中C、B点,使用菜单“编辑”中的“操作类按钮”的“移动”命令,选择中速,移动到目标位置,设置出按钮“移动C→B”;同理设置出按钮“移动C→A”。
单击按钮“移动C→B”,就可以显示D点的运动轨迹,如图1所示。
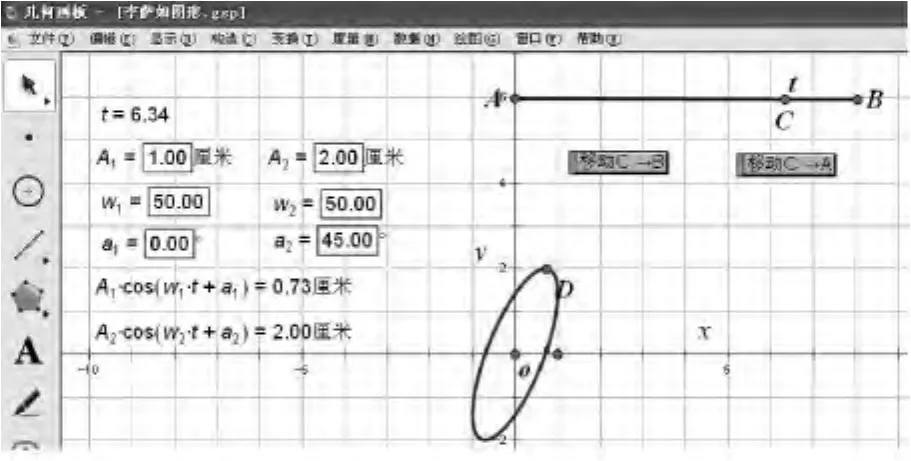
图1 两个相互垂直的同频率的谐振动的合成D点的轨迹
改变参数,可以得到D点不同的轨迹,图2是两个相互垂直的同频率而不同相位差的谐振动的合成,图中只需保留了D点的轨迹,其他元素都隐藏。
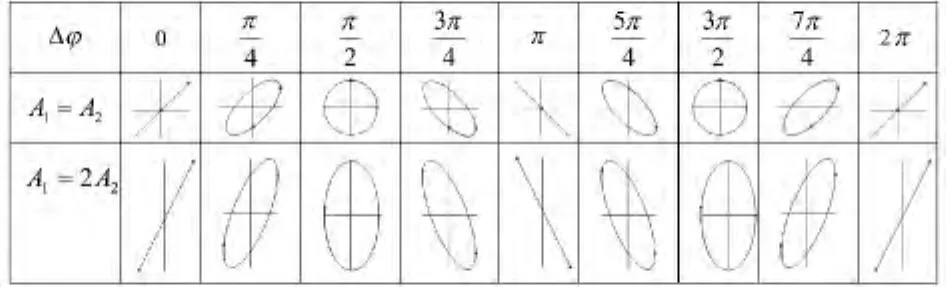
图2 两个相互垂直的同频率而不同相位差的谐振动的合成Δφ=φ20-φ10
4 两个相互垂直的频率成整数比的谐振动的合成
设置 w1w2为 5 2,A1=2A2,得到图3。
图3两个相互垂直的w1w2为5 2的谐振动的合成(A1=2A2)
依次取 w1w2为2 1、3 1、3 2 和5 2,依次2π,取 A1=2A2,得到图4。
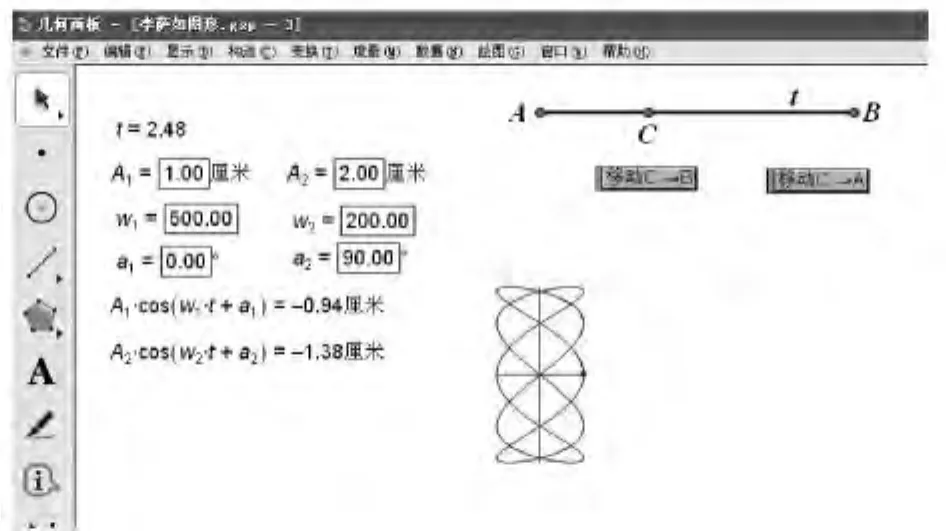
图3 两个相互垂直的w1w2为52的谐振动的合成(A1=2A2)

图4 两个相互垂直的频率成整数比的谐振动的合成(Δφ=φ20-φ10A1=2A2)
若以N1和N2分别表示李萨如图形与外切水平线及外切垂直线的切点数,则其切点数与正弦波频率之间有如下关系:w1w2=N1N2。
本文中使用的谐振动方程合成的方法,特别是设置变量t的方法,适用于其他简谐振动的多种关系图示。[4-5]
[1] 马文蔚.物理学·下册(第四版)[M].北京:高等教育出版社,1999:23-26.
[2] 赵艳.基于Matlab示波器原理的演示[J].大学物理实验,2013,26(16).
[3] 兰明乾.用几何画板描绘李萨如图形[J].实验科学与技术,2008(3):31-33.
[4] 王明美.几何画板在一维简谐振动的合成教学中的应用[J].合肥师范学院学报,2013,12(6):69-70.
[5] 王明美.“几何画板”绘制机械振动的关系图示[J].大学物理实验,2013,26(4):69-71.

