用惠斯登电桥实验系统与SPSS标定电阻

王 锋，王新春，岳开华，祝飞霞，司民真

(楚雄师范学院，楚雄 675000)

对A类，若测量为8次，测量结果服从t分布［8］，当 p=0．95 时，tp=2．36，即

电桥是一种利用电位比较的方法进行测量的仪器，因为具有很高的灵敏度和准确性，在电测技术和自动控制测量应用极为广泛［1］。对直流电桥［2］的研究，是大学物理实验最重要的实验内容之一。通过查阅献［3-5］可知，直流单电桥(惠斯登电桥)适于测量10～106Ω中阻值电阻。用直流电桥来测量电阻，通常使用比较的方法进行实验数据的测量。用置信概率为95%的不确定度估算方法对测量数据及实验结果进行分析与评价，使得实验结果更加可靠。同时，引入Spss［6］的曲线估计功能去分析实验数据，可以明显减小因仪器或人为因素带来的误差，使得实验结果更为合理。

1 实验装置及调试

实验装置见图 1，主要由惠斯登电桥、YB1733A2A直流稳压电源、ZX21型多盘十进电阻箱(99999．9Ω)、标准电阻、BX7-13 型滑线变阻器、单刀单掷开关、检流计等组成。

如图1所示，断开单刀单掷开关，调节检流计指针与标尺的零刻度线重合，调节两个滑动变阻器达到保护电路的作用，选定标准电阻(RX=2 400 Ω)，电阻箱(RS)的值归零，记录下来。

闭合单刀单掷开关、移动惠斯登电桥滑动触头，得到滑动触头左右两端的值(L1和L2)。然后调节电阻箱(RS)，使检流计指针与标尺的零刻度线再次重，可在电阻箱上得到一个R为RS;L1和L2用米尺测出，RS从电阻箱上读出。

图1 用直流电桥测电阻实验装置图

2 实验原理

2．1 测量原理

实验电路原理如图2所示，一般情况下，桥路上检流计中有电流通过，因而检流计的指针有偏转。适当调节改变RS的大小，可使C、D两点的电位相等，此时流过检流计G的电流IS=0，电桥处于平衡状态。即有

图2 实验装置的电路图

联立(1)、(2)式可得

实际测试中，R1、R2用一根均匀电阻丝替代，RS为电阻箱。而电阻定义式［7］

将(4)、(5)代入(3)可得

设电阻和长度的综合量Y=L1RS，则(6)式可简化为

实验中使电桥始终处于平衡状态下(改变L1、L2的同时应调整RS)。L2用米尺测量，从而可得(L2i);L1用米尺测量，RS由电阻箱读取，由此可得电阻和长度的综合量(Yi)。应用SPSS的线性估计功能，试图去分析综合量(Yi)与长度量(L2i)的线性相关性，从而标定出电阻的RX，并对其不确定度做出估算。

2．2 直流电桥测电阻的不确定度分析

直接测量r，其不确定度可分A类、B类进行评定。测量列平均值的标准偏差［8］为

对A类，若测量为8次，测量结果服从t分布［8］，当 p=0．95 时，tp=2．36，即

对于B类分量，若其误差极限为Δ，仪器误差服从均匀分布［8-9］，当 p=0．95 时，rp=1．96，那么

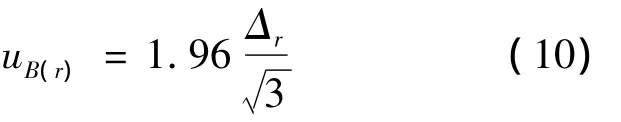
(9)式中的 r分别表示 L1、L2、RS。

直接测量r的合成不确定度为

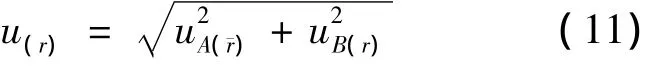
对于间接测量y=f(r1，r2，．．，rn)，则RX的标准不确定度uc(y)为［10］

y的相对不确定度ur(y)为

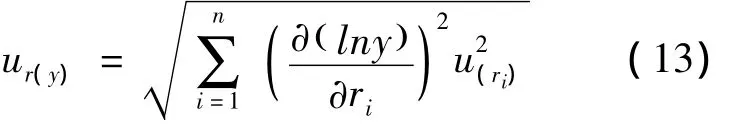
考虑(7)、(13)式，被测电阻RX的相对不确定度为

3 实验数据处理

3．1 测量数据极其处理

表1 触点在不同位置下RS的测量值

表2 综合量Yi与长度量L2i的实验数据

3．2 用Spss软件分析Y-L2定标曲线

将表2中的数据输入SPSS软件中，以L2为自变量，Y为因变量，由SPSS的曲线估计功能可得其定标曲线为

所得曲线见图5。

图3 Y-L2定标曲线

3．3 被测电阻不确定度的估算

根据图3的Y-L2定标曲线，在直线上适当取样 L21、Y1;L22、Y2值，合理估算 RX的不确定度。由(15)可得

由图 3 直线上 L21、Y1;L22、Y2取样值，可得

由(14)、(17)可得

由图3不确定度评定取样点 L21、Y1;L22、Y2，结合(16)、(17)、(18)可得表3实验结果。

表3 用直流电桥测电阻的实验结果

4 分析与讨论

从测量原理所得(7)式可知，只要测量条件具备，理论上有电阻和长度的综合量(Y)与长度量(L2)应该具有线性关系，若能从实验的角度研究出Yi-2i线性关系，必然可以标定出被测电阻的值，这在实验的测量原理上具有一定的创新性。

由表2实验数据，应用SPSS线性估计功能分析得定标方程(15)式及其图3，并得到Y-L2定标曲线图。得出了电阻和长度的综合量(Yi)与长度量(L2i)成线性关系，实验所得定标方程(15)式及图3实验曲线与理论分析(7)式具有一致性。

由表3数据，应用SPSS曲线估计功能得到定标方程(15)式，可得被测电阻值为 2．401×103Ω，对比表1所给定标被测电阻2．400×103Ω，二者具有较好一致性，表明实验所拟合的Y-L2直线是客观的。

为了能更好的实现实验数据线性分析的合理性。实验中应使电阻总长(L1+L2)保持在100 cm不变，选择有效长度L1、L2的改变量为15 cm，使得电阻箱RS值可控在1～4．5 kΩ之间变化，这样可使测量结果较为可靠，实验结果更为合理。

能够得到较为理想的(15)式、图3、表3的实验结果，除了借助了强有力的计算机辅助(SPSS软件)分析手段外，表明所测量数据(表1)的质量较高，说明有效长度L1、L2的选择较为合理，电阻箱Rs的调整较为细致，使因仪器或人为因素所致的偶然误差与系统误差已降为较小。

对照(15)式中的斜率为2．401×103Ω与表1所给定标称电阻值2．400×103Ω，它们具有较好吻合度，尤其查看表3中被测电阻的实验结果，由该实验方案所得灵敏度的实验值只在千分位上可疑，而以往用灵敏度特性研究的实验方案所得灵敏度的实验值一般为十分位或百分位上可疑。说明应用SPSS的线性分析功能标定被测电阻的阻值，是可以提高测量数据及实验结果的分析精度，且数据的处理过程及结果直观有效。因此，该实验方案值得推广。

［1］ 张海峰，爱玲．直流电桥输出非线性误差消除研究［J］．安阳工学院学报，2007(1):96-99．

［2］ 张丽丽．直流电桥的原理及应用［J］．电子科技，2013(2):19．

［3］ 张明金．对直流电桥测量电阻的分析［J］．中国仪器表，2005:114-116．

［4］ 康裕荣，康向东．提高直流单电桥测电阻准确度的讨论［J］．西安科技大学学报，2004，9(24):3．

［5］ 吕光明．直流电桥电阻箱高准确度测量方法的研究［J］质量技术监督研究，2013(2)．

［6］ 宋志刚．SPSS 16．0 guide to data analysis［M］．北京:人民邮电出版社，2008:115-186．

［7］ 马俊杰．用数字万用表探究电阻定律［J］．物理科学探究，2006(21)．

［8］ 刘建伟，王新春．用改进的单摆实验系统与spss标定重力加速度［J］．大学物理实验，2013，8(24):56-57．

［9］ 严箫，王新春，岳开华，等．用等偏法与SPSS研究灵敏电流计的特性［J］．大学物理实验，2014(2):65-68．

［10］刘才明．大学物理实验中测量不确定度的评定与表示［J］．大学物理，1997，16(8):21-23．