箕斗定量装载系统缓冲仓的强度和稳定性分析

王囡囡，胡志鹏，王积永

（1.山东建筑大学机电工程学院，山东济南250101；2.山东省高校机械工程创新技术重点实验室，山东济南250101；3.国家知识产权局专利局专利审查协作河南中心，河南郑州450002）

箕斗定量装载系统缓冲仓的强度和稳定性分析

王囡囡1，2，胡志鹏3，王积永1，2

（1.山东建筑大学机电工程学院，山东济南250101；2.山东省高校机械工程创新技术重点实验室，山东济南250101；3.国家知识产权局专利局专利审查协作河南中心，河南郑州450002）

缓冲仓是箕斗定量装载系统中的关键部件，物料的不同载荷作用将导致缓冲仓发生破坏。文章根据承载能力极限状态和壳体薄膜理论研究缓冲仓的强度和稳定性条件，通过ANSYSWorkbench研究缓冲仓的应力分布状态，利用Linear Bucking模块对缓冲仓进行线性屈曲分析。结果表明:缓冲仓的最大等效应力并不是位于筒仓最底部与环梁相接处，而是距离环梁约1.8 m处，此处引起仓壁应力的急剧变化，产生“象腿”破坏现象；缓冲仓发生结构屈曲破坏主要由径向大变形引起，随着储料载荷的增大，结构在发生屈曲破坏前已出现强度破坏，缓冲仓的主要破坏形式为强度破坏。

缓冲仓；强度分析；稳定性分析；屈曲分析；ANSYSWorkbench

0 引言

箕斗定量装载系统是广泛应用于建筑、煤炭、粮食、电力、化工等行业的贮装与计量装置，其工作要求是实现定量、定时、准确和快速的装载［1］。目前，在煤矿领域，综合PLC和液压控制技术提高了装载系统的自动化称量技术，但在定量斗装卸过程中，一方面含水量较高的粉末煤质经常导致定量斗堵塞滞煤现象，另一方面煤块对定量斗有一定的冲击作用，在长期频繁的工作下，该冲击瞬时力将严重影响称重系统的精度［2］。针对上述问题，在现有装载系统的基础上，提出一种新的结构设计方法，即在定量斗上方安装一个小型缓冲仓。缓冲仓属于筒仓结构，在实际使用中经常出现筒仓破坏现象，即使在技术较为先进的欧美国家，也常报道筒仓破坏事故，如1997年法国的一起粮食筒仓倒塌事故甚至造成了严重的人员伤亡［3］。

因此，筒仓的强度和稳定性是需要考虑的重要指标，Janssen提出的静压理论至今仍是筒仓设计规范的基础［4］；八旬隆道研究筒仓仓壁压力时指出筒仓卸料时由于流动中的散体形成的拱体，会在仓壁上产生异常超压，考虑了散体重力流动规律与仓壁压力变化的关系［5］；Sanjay等研究了非粘性应力颗粒对倾斜储料仓壁的静载荷时指出储料仓的应力分布预测在工业应用中非常重要，推导出有效应力系数表达式［6］。常双君分析了大直径圆筒仓结构边缘受力效应，根据计算模型得到相应的沿仓壁高度的边缘效应分布曲线［7］；俞激采用数值分析方法研究了仓壁柱支承钢筒仓的强度和稳定性，详细分析了筒仓各主要几何参数以及初始几何缺陷对结构受力行为的影响［8］。

上述研究成果主要针对筒仓结构的研究，而对矿井中箕斗定量装载系统的缓冲仓的研究甚少，文章根据实际工况设计缓冲仓的结构形式，基于Janssen理论并结合相关规范对设计的缓冲仓进行强度和稳定性计算，研究定量斗在储料静载作用下和卸料装料过程中动载作用下的仓壁的受力情况，进一步利用有限元分析软件对缓冲仓强度和稳定性屈曲分析进行分析，以保证筒仓结构能够安全可靠的运行。

1 缓冲仓参数

根据相关工况、GB 50077—2003《钢筋混凝土筒仓设计规范》［9］和GB 50322—2001《粮食钢板筒仓设计规范》［10］，设计缓冲仓的主要结构参数是:筒仓内径为2800 mm，筒仓高为2000 mm，漏斗卸料口直径为1000 mm，漏斗高为1000 mm；当仓中储料选取烟煤时，其物料参数有:重力密度γ＝8.0～11.5 kN／m3，内摩擦角φ＝33°，对钢板仓壁的摩擦系数。

2 缓冲仓强度与稳定性计算

2.1 载荷计算

根据承载能力极限状态理论对筒仓进行结构设计，则储料作用于缓冲仓仓壁的荷载组合分以下几种情况［11］:

作用于单位面积仓壁上的水平压力组合由式（1）计算为

无风载时作用于单位面积仓壁上的竖向压力组合由式（2）计算为

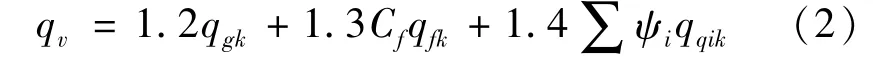
有风载时单位面积仓壁上的竖向压力组合由式（3）计算为

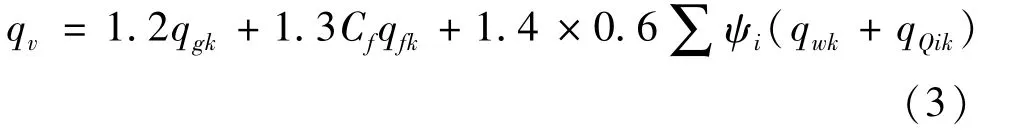
式中:Ch为水平压力修正系数；Phk为仓壁水平压力，kN／m；Cf为竖向压力修正系数；qgk为永久载荷作用于仓壁单位周长上的竖向压力，kN／m；qfk为储料作用于仓壁单位周长上的总摩擦力，kN／m；ψi为可变荷载组合系数；qQik为可变载荷作用于仓壁单位周长上的竖向压力，kN／m；qwk为风荷载作用于仓壁单位周长上的竖向压力，kN／m。

2.2 强度计算

2.2.1 筒仓强度计算

缓冲仓由筒仓和漏斗组成。对于不设加劲筋的筒仓仓壁，根据薄膜理论计算筒仓仓壁的强度。

考虑储料对仓壁的水平压力作用时，仓壁的环向拉应力由式（4）计算为

考虑仓壁承受的竖向压力作用时，其竖向压应力由式（5）计算为

在竖向压力和水平压力的共同作用下，应力折算由式（6）计算为

式中:t为仓壁厚度，m；f为材料抗压或抗拉强度，MPa。

由于缓冲仓位于井下硐室中，其上部没有设置其他机构，因此计算缓冲仓载荷时，只考虑仓内储料对缓冲仓的作用，根据缓冲仓的相关参数，计算得到缓冲仓所承受的载荷，并进行强度计算，其结果见表1。

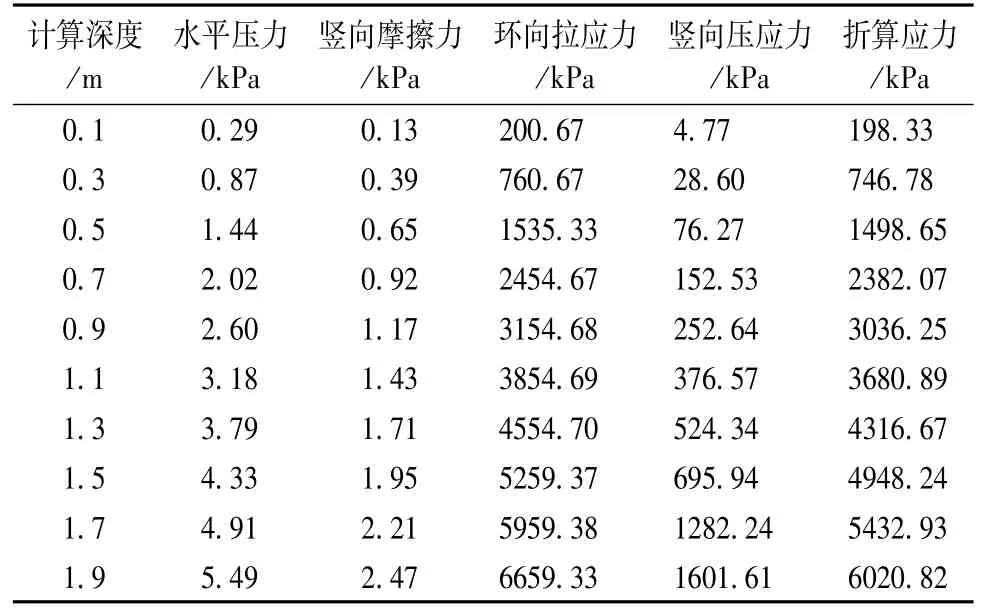
表1 缓冲仓强度计算结果

2.2.2 漏斗强度计算

根据漏斗的结构特点按照圆锥壳对薄膜内力进行强度计算。漏斗的计算简图如图1所示。

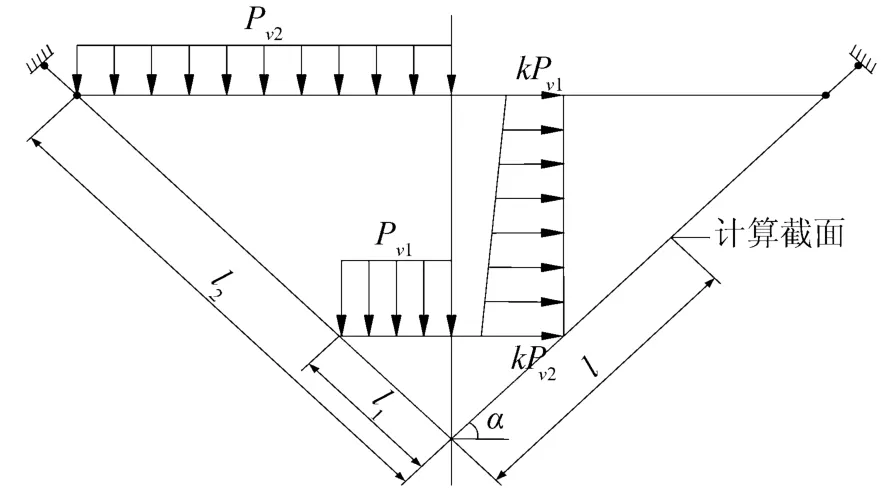
图1 漏斗计算简图

截面处单位宽度斜壁上的环向拉力设计值由式（7）计算为

截面处单位宽度斜壁上的径向拉力设计值由式（8）计算为

式中:γQ为储料荷载分项系数；l为计算截面到锥顶的距离，m；pv1为储料作用于漏斗底部单位面积上的竖向压力值，Pa；pv2为储料作用于漏斗顶部单位面积上的竖向压力值，Pa。

漏斗壁在薄膜内力作用下双向受拉，其强度由式（9）和式（10）计算为

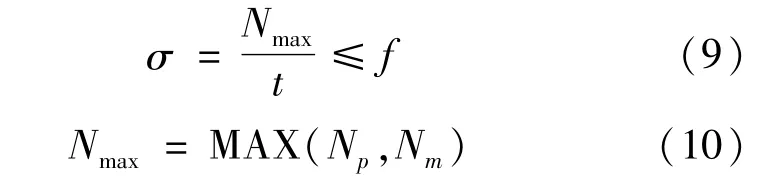
式中:t为漏斗壁厚度，m。

将漏斗基本参数代入上述各式中得到漏斗受力计算结果见表2。

表2 漏斗受力计算结果

2.3 稳定性计算

筒仓仓壁在轴向荷载的作用下，根据薄壳结构弹性稳定性理论进行稳定性计算［12］。

在轴向压力作用下由式（11）计算为

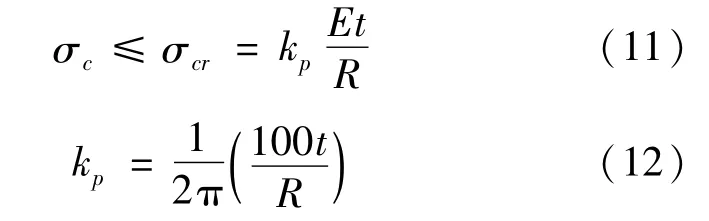
在轴向压力和储料的水平压力共同过用下由式（13）和式（14）计算为

式中:σc为仓壁的竖向压应力，Pa；σcr为仓壁失稳临界应力，Pa；E为材料弹性模量；R为筒仓半径，m；kp、k为稳定系数。根据式（13）和式（14）计算得到仓壁的失稳临界应力为614 MPa，对比表1中仓壁竖向压应力的计算结果，其最大值远小于失稳临界应力，因此，仓壁稳定性满足设计要求。

3 缓冲仓强度分析

3.1 缓冲仓有限元建模

不考虑焊接因素对结构的影响，将仓壁看作一个整体；忽略螺栓等连接件对结构的影响；同时忽略结构件上的圆角、倒角等次要因素，首先利用Pro／E软件建立缓冲仓的三维模型，然后导入ANSYS Workbench中，采用智能网格方式进行划分，为了获得准确结果，根据强度计算结果设置缓冲仓模型关键位置的网格大小，即进行局部细化，缓冲仓的有限元建模［13-14］，如图2所示。

3.2 缓冲仓强度分析

3.2.1 载荷与边界条件

除结构本身的自重外，缓冲仓所承受的荷载主要来自储料对缓冲仓仓壁的作用，而缓冲仓仓壁主要承受来自储料的水平压力和竖向摩擦力，漏斗主要承受储料的重力作用。同时，为了考虑缓冲仓装卸料过程的动态作用对结构强度的影响，在进行荷载计算时，在静态压力的计算结果上乘以动态压力修正系数，并考虑荷载的效应组合，如图3所示为缓冲仓加载效果图。

图2 缓冲仓有限元模型图

由于缓冲仓通过环梁置于硐室内的支座上，因此将环梁底面设置为固定全约束，缓冲仓上端仅对其环向及径向的位移进行约束，竖向位移保持自由。

3.2.2 强度分析结果

对缓冲仓施加荷载和边界约束后，进行强度分析，缓冲仓等效应力分布图如图4所示。

图4 缓冲仓等效应力分布图

从图4中可以看出，缓冲仓的最大等效应力出现在筒仓部分下端靠近环梁处的内壁上，最小应力位于筒仓顶端。从最大应力的数值可以看出，材料远未达到屈服极限，强度满足要求。总体来看，筒仓部分上部的应力较小，中部应力变化较为均匀，而底部应力相对较大，而漏斗部分整体应力较大，这是因为漏斗部分几乎承受了缓冲仓内物料的所有重力荷载。

图5所示为缓冲仓内壁上沿母线方向的应力变化，图5（a）描述了筒仓内壁环梁以上部分的应力变化，其中x坐标表示距离筒仓顶端的深度，图5（b）描述了整个漏斗内壁沿母线的应力变化，其中x坐标表示与漏斗顶端的距离。

图5 缓冲仓应力变化曲线图

从图5（a）中可以看出缓冲仓筒仓部分内壁的最大应力并不是位于筒仓最底部与环梁相接处，而是出现在距离环梁大约0.18 m处，应力曲线在该位置发生突变，这是由于筒仓底部的位移受到限制，储料水平压力与竖向摩擦力的共同作用使该处仓壁出现了弯曲内力，从而引起仓壁应力在该处出现急剧变化。在图5（b）中，漏斗顶部的应力很小，在距离顶部约0.2 m处发生突变迅速增大并出现最大值，这是因为强度计算时，没有考虑环梁对漏斗壁应力的影响所导致的。

3.3 缓冲仓稳定性分析

3.3.1 线性屈曲分析

缓冲仓属于典型的圆柱薄壳结构，当外载荷较大时，应力集中出现在环梁附近，此时缓冲仓除了出现强度破坏外，仓壁承受的竖向力也可能导致仓壁发生屈曲破坏，其中，该竖向力来自仓顶结构的自重和储料作用于仓壁上的竖向摩擦力。

利用Linear Bucking模块对缓冲仓进行线性屈曲分析［15］，根据静力分析结果进行特征值屈曲分析，得到屈曲荷载系数和屈曲模态。

3.3.2 稳定性分析结果

在Workbench软件中首先将Linear Bucking模块拖入静力分析模块（Static Structural）的Solution项，以实现两模块之间的连接，然后进行特征值求解，得到缓冲仓在储料荷载作用下的屈曲分析结果。图6所示为缓冲仓一阶屈曲模态，图7所示为相对应的沿母线方向的屈曲变形曲线，其中，x、y、z分别为缓冲仓内壁径向位移、轴向位移和切向位移。

图6 缓冲仓一阶屈曲模态图

从图6、7可以看出，在储料荷载作用下缓冲仓屈曲荷载系数为297.57，且相对变形量最大值为1.0003 mm，因此储料作用于仓壁的荷载远小于结构发生屈曲失稳时的临界荷载；结构发生屈曲失稳时的变形主要出现于筒仓部分，而漏斗仓壁几乎不发生失稳变形；变形区域集中在距离环梁0～0.7 m范围内，切向变形与轴向变形的数值较小，最大变形出现于距离环梁约0.25 m处，该位置与强度分析中的仓壁最大应力和最大变形位置接近，表明缓冲仓发生结构屈曲破坏主要是由径向的大变形引起的，即强度分析中提到的“象腿”破坏现象，基于最大变形位置，为后续缓冲仓的加固设计提供理论依据。

图7 缓冲仓屈曲变形曲线图

4 结论

文章根据实际工况对缓冲仓进行结构设计，根据承载能力极限状态，利用薄膜理论，对筒仓在不同载荷作用下的强度进行计算，进一步根据薄壳结构弹性稳定性理论对缓冲仓进行了稳定性计算；通过ANSYSWorkbench对缓冲仓进行强度和稳定性分析可知:

（1）缓冲仓结构的最大应力和最大变形均出现在靠近环梁的仓壁处，最大应力出现在0.18 m处；

（2）缓冲仓竖直仓壁承受的轴向力是结构发生稳定性破坏的主要诱因，较容易出现稳定性破坏的区域位于竖直仓壁上靠近环梁处；由于缓冲仓承受的轴向力较小，其稳定性较高，破坏的主要形式为强度破坏。

［1］ 滕锦光，赵阳.大型钢筒仓的结构行为与设计［J］.土木工程学报，2001，34（2）:46-53.

［2］ 孟凡喜.非接触式称重技术在主井定重装载自动控制系统中的应用［J］.能源技术与管理，2009（4）:131-132.

［3］ 佟越波.电子计量装置在矿井箕斗定量装载的应用［J］.计量测试，2002（12）:79-81.

［4］ Janssen H.A..Uber getreidedruck in silozellen［J］.Zeitschrift Des Vereines Deutscher Ingenieure，1985，39（35）:1045-1049.

［5］ 八寻隆道.粉体的初期充填状态和贮槽的异常壁压［J］.粉体工学志，1994，31（12）:850-861.

［6］ Sanjay K.S.，Jeffrey G.L..Stresswithin a cohesionlessgranular fill in a storage vesselwith slopingwalls during initial static loading［J］.Powder Technology，2009，192:389-393.

［7］ 常双君.大直径圆筒仓结构边缘受力效应分析［J］.中北大学学报，2010，31（2）:200-204.

［8］ 俞激.仓壁柱承钢筒仓结构的稳定性能和强度的研究［D］.杭州:浙江大学，2005.

［9］ GB 50077—2003，钢筋混凝土筒仓设计规范［S］.北京:中国计划出版社，2003.

［10］GB 50322—2001，粮食钢板筒仓设计规范［S］.北京:中国计划出版社，2001.

［11］谢醒悔，韩选江，叶湘菡.现代予力混凝土结构设计理论及应用［M］.北京:机械出版社，2007.

［12］Timoshenko S.P.，Wbinowsk-Kriegr S..Theory of Platesand Shells［M］.New York:MeGraw-Hill，2011.

［13］张天.基于ANSYSWorkbench的电动车车架疲劳分析［J］.山东建筑大学学报，2013，28（6）:570-574.

［14］曾丁，黄文彬，华云龙.筒仓壁压的有限元分析［J］.农业工程学报，1998，14（2）:142-146.

［15］赵晓伟，鹿晓阳，王磊.重心插值配点法分析梁屈曲问题［J］.山东建筑大学学报，2009，24（2）:142-144.

（责任编辑：李雪蕾）

Strength and stability analysis of surge bunker in skip loading system

Wang Nannan1，2，Hu Zhipeng3，Wang Jiyong1，2

（1.School of Mechanical and Electronic Engineering，Shandong Jianzhu University，Jinan 250101，China；2.Key Laboratory of Mechanical Engineering＆Innovation Technology in Universities of Shandong，Jinan 250101，China；3.Patent Examination Cooperation Center of the Patent Office，SIPO，Henan 450002，China）

In traditional skip weight-fixed loading system，in order to improve the coal-stagnating and the coal's impact effect on skip，a surge bunker is designed on top of hopper.Surge bunker is a key component in skip loading system，and different loads from materials will lead to structural damage.Therefore，according to limit status of bearing capability and membrane theory of shells，strength calculation and stability analysis of surge bunker is studied.Thereafter，bunker＇s stress distributing state is conducted with ANSYSWorkbench，and based on the results，the linear buckling analysis is carried out by employing the linear bucking module.The results show that the maximum stress of bunker has certain distance from ring beam which is not located in the joint of bottom and ring beam，and the rapidly change of stress leads to the“elephant foot”damage.The yield bending damage is caused by radial deformation，and with the increase of load，the strength destroy has produced before yield bending damage，which identify themajor failure of surge bunker is strength failure.

surge bunker；strength analysis；stability analysis；buckling analysis；ANSYS Workbench

TU312

A

1673-7644（2014）06-0535-06

2014-06-09

山东建筑大学博士科研基金项目（XNBS1325）

王囡囡（1983-），女，讲师，博士，主要从事结构设计及优化分析等方面的研究.E-mail:wangnannan_333＠163.com