零方程湍流模型用于城市微气候的模拟研究

刘吉营，郭敏，斯雷布里奇·伊莲娜，达维多维奇·丹科

（1.山东建筑大学热能学院，山东济南250101；2.山东建筑大学山东省建筑节能技术重点实验室，山东济南250101；3.山东省可再生能源建筑应用技术重点实验室，山东济南250101；4.美国马里兰大学机械工程系，美国马里兰州20742；5.胡贝尔工程林木公司，美国商务城30530）

零方程湍流模型用于城市微气候的模拟研究

刘吉营1，2，3，*，郭敏1，2，3，斯雷布里奇·伊莲娜4，达维多维奇·丹科5

（1.山东建筑大学热能学院，山东济南250101；2.山东建筑大学山东省建筑节能技术重点实验室，山东济南250101；3.山东省可再生能源建筑应用技术重点实验室，山东济南250101；4.美国马里兰大学机械工程系，美国马里兰州20742；5.胡贝尔工程林木公司，美国商务城30530）

室外微气候环境对城镇人居环境和建筑能耗有重要影响，数值模拟技术作为快速的预测方法能有效评价社区规划的优劣。文章选用风洞实验数据对湍流涡粘度表达式进行优化，提出新的零方程湍流模型（Zero-EQ），并与两方程湍流模型（MMK）、大涡模拟（LES）和风洞实验数据进行对比分析；通过对寿安新城区零方程湍流模型的应用分析，探讨该模型应用于实际工程项目的可行性。结果表明:在同等计算机配置下，Zero-EQ模型比MMK模型快60%，是LES模型计算所需时间的1／15，能有效地预测不规则建筑群的流场分布；通过分析不同地形区域的风热环境特点，Zero-EQ模型可快速预测城镇微气候环境，为城区规划设计提供合理建议。

零方程湍流模型；城市微气候环境；计算流体动力学；城市规划设计

Key words:zero-equation turbulence model；microclimate urban environment；computational fluid dynamics；urban planning and design

0 引言

在城镇化快速发展的过程中，室外人居的风、光、热、污染物等微气候生态环境日益受到广泛关注，而数值模拟技术作为最有效的预测方法之一，已成为评价低碳生态社区规划优劣的重要方法［1-3］。目前，应用于城市微气候环境数值模拟最广泛的两种湍流模型分别是基于雷诺平均的 RANS（Reynolds-Average Navier-Stokes Equations）模型和大涡模拟LES（Large Eddy Simulation）。时至今日，由于计算机资源的限制，LES仍限于简单的建筑模型或者相对较小的区域。通过对比分析常用湍流模型预测城市风环境的优劣，在较小CPU能耗情况下，RANS模型在非近壁区和非稳态流动时模拟结果不理想，而LES需要较大的CPU消耗才能取得相对较好的预测结果［4］。而在实际情况下，对于城镇区域大小的空间尺度，选择RANS模型仍需要较大的计算机资源才能获得可以接受的预测结果。因此，如何能够快速且相对准确地预测城市微气候环境状况，提供给工程师和设计师准确的信息，满足工程需要，将成为本课题的重点研究方向。近年来，有一种已经被证明能够快速有效地模拟室内微气候环境的零方程湍流模型（Zero-EQ），正逐步应用于室外微气候环境的预测［5-8］。

目前，已有的Zero-EQ模型大多利用普朗特混合长度理论，而混合长度理论主要应用于自由剪切流，适用于简单的边界层流动。因此，Van Driest提出了壁面衰减函数来解决管道流的流动问题［9］，Cebeci等提出了一个综合考虑高速流动、低雷诺流动和管道流等两层的Zero-EQ模型［10］，而Baldwin等则提出了类似的两层Zero-EQ模型来解决管道流［11］。Chen等通过设置特定的湍流动能，提出了新的基于室内环境研究的涡粘度表达式［5］。以上Zero-EQ仅适用于特定的边界层流动或小尺度下的室内环境的研究，对于城镇尺度下的大气边界层，显然不适用。现有应用于室外微气候环境预测的Zero-EQ是基于单栋建筑的风洞试验推导出来的，仅局限于室外单栋建筑或规则建筑群的微气候环境［8］。对于不同高低、间距和位置等不规则分布的建筑群或实际城镇社区，因其复杂的建筑扰流与多变的特征长度尺度，目前鲜有涉及［12］。因此，文章通过分析风洞实验数据，研究不规则建筑群的流场变化，推导出优化的湍流涡粘度表达式，提出新的零方程湍流模型。通过与两方程湍流模型MMK（Murakami-Mochida-Kondo）、LES和风洞实验对比，验证其具有相对准确和快速的优势，并应用于某城镇低碳生态建设规划设计，具有非常广泛的应用前景［13］。

1 零方程模型优化

基于非稳态不可压连续性和动量的雷诺平均Navier-Stokes方程（RANS）可用式（1）或式（2）表示为

式中:ui为分量速度，m／s；xi为分量方向，m；t为时间，s；ρ为流体密度，kg／m3；μt为湍流涡粘性系数，Pa·s；β为热膨胀系数，1／K；为雷诺应力，Pa；T0为操作温度，℃；T为流体温度，℃；gi为重力加速度，m／s2。

在式（1）（2）中，由于雷诺应力是一个未知参量，为了能解上述湍流方程，雷诺应力选用Boussinesq假设，把雷诺应力与平均应变率和湍流涡粘度（μt）相关联（即常说的线性涡粘度模型），得到式（3）:

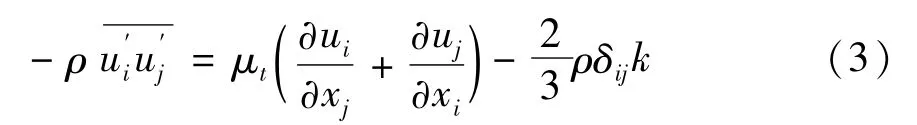
式中:δij是克罗内克符号；k是湍流动能，m2／s2；ρδijk是一种用张量代数来表达的线性本构关系，用于求解雷诺应力。

为了能够求解雷诺应力，对两方程湍流模型而言，湍流涡粘度（μt）与湍流动能（k）和湍流耗散率（ε）或者湍流特定耗散率（ω）相关。因此，为了同时解k和ε，需要两个封闭的k和ε方程来计算，而对于两者不同的处理策略，形成了目前众多不同的两方程湍流模型。如果只选用k方程来处理雷诺应力，即为一方程湍流模型；如果不选任何方程，只是采用代数算法公式来表述雷诺应力的话，即称算法模型，也就是Zero-EQ模型。

Zero-EQ模型在利用Boussinesq假设来求解雷诺应力的过程中，忽略k微分方程，而采用简单算法方程，则式（3）简化为式（4）

为求解湍流涡粘度（μt），依据Prandtl的混合长度理论，将式（4）简化为单向的二维边界层，其平均的雷诺应力与平均速度梯度有关。在本实验中，仅考虑雷诺在垂直方向上的顺流速度梯度，式（4）可进一步简化为式（5）

式中:U为垂直方向上的顺流速度分量，m／s。通过处理建筑周围流场各测点数据，得到相应的雷诺应力和顺流速度分量梯度，计算出各测点的湍流涡粘度分布。通过分析涡粘度数据，推导出优化的零方程湍流涡粘度表达式，如式（6）至式（8）所示

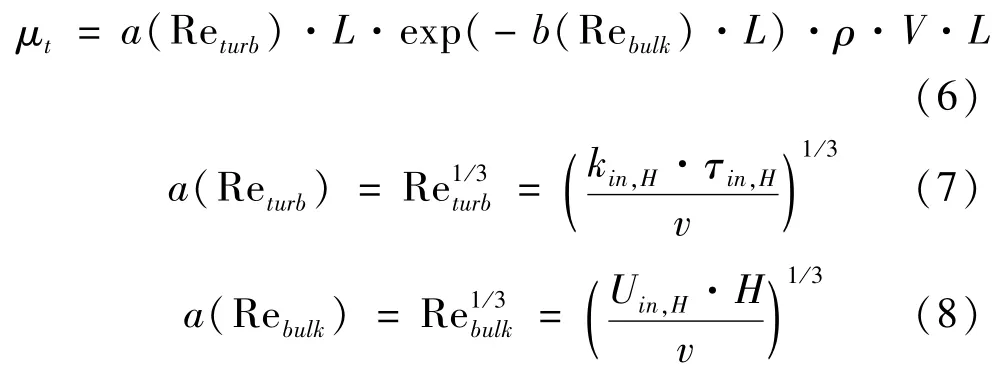
式中:Returb是湍流雷诺数；Rebulk是主导雷诺数；L是积分湍流尺寸长度，m；H为区域内平均建筑高度，m；V是建筑周围流场局部计算点的速度大小，m／s；kin，H是在建筑H高度处入口湍流动能，m2／s2；τin，H是在建筑高度H处入口湍流时间尺度，s；Uin，H是建筑高度H处入口速度大小，m／s；v是动力粘度，m2／s；a和b为涡粘度表达式系数。

2 湍流模型对比分析

2.1 湍流模型介绍

当标准k-ε湍流方程预测流体经过钝体建筑时，存在一些误差，比如过高预测碰撞区域的湍流动能k等，因此Kato等通过修改湍流动能产出项Pk，提出修正的两方程湍流模型（LK）［14］；但是LK模型在研究湍流雷诺应力和Pk时仍存在数值的不稳定性现象。因此，Tsuchiya等通过在涡粘度表达式中添加修正参数，而非湍流动能产出项，得到了基于LK模型修正的MMK模型［13］。考虑到LES计算需要大量的计算机资源，作为修正的k-ε湍流模型:LK和MMK模型，因其相对快速而又相对准确地预测建筑环境，目前已被大量地应用于城市风热环境的研究中［15］。在LES计算中，选择Smagorinsky常数Cs＝0.12用于求解亚格子涡粘度。文章选用MMK模型、LES模型，与Zero-EQ模型和风洞实验数据对比，分析Zero-EQ模型的优劣。

2.2 风洞实验介绍

文章选用宾夕法尼亚州立大学航空航天工程系的风洞实验室开展实验［12，16-17］（如图1所示），风洞试验台长度约6 m、宽度为0.6 m、高度为0.9 m。在Qian研究单栋建筑的基础上［8］，选择四栋毗邻的学生公寓作为研究对象，其中每栋建筑长28 m、宽20m和高30 m，建筑模型缩尺比例为1:250，雷诺数为80000。

缩尺模型周围的水平和竖直测点分布图如图2所示。在选择水平测点时，尽量选择建筑中心侧的位置。根据缩尺模型分布和周围流场的特点，布置了水平位置上的八横行（Y1至Y8）和八纵列（X1至X8）。研究选取对模型下游流场影响比较大的四横行Y3、Y4、Y5和Y6作为研究对象，除因位置原因无法测试外，总计26个水平测点。其中测点X1Y1、X1Y4、X1Y8主要用于入口边界的速度和湍流强度边界条件。

2.3 CFD模拟设定

在数值计算时，减少计算区域上游的距离满足实际风洞边界测点与第一个建筑的距离要求，即计算区域距上游第一个建筑1 H长度，距下游最后一个建筑12 H长度，而侧面和垂直区域受实际风洞实验条件的限制，分别为2.5 H高度和3.6 H高度，计算模型如图3所示。MMK模型和Zero-EQ模型结构化网格数为140×110×100。采用网格收敛指数GCI对网格相关性分析，即:GCI［fine］＝FS｜ε｜／（rp-1）。计算上游第一个建筑迎风面的表面摩擦系数Cf，分别选取粗糙网格（120×90×85，Δ1），中等密度网格（144×110×100，Δ2）和加密网格（170×132×120，Δ3）。结果表明:GCI［3，2］＝3.18%（加密网格对比中等密度网格）和GCI［2，1］＝7.54%，GCI［3，2］相比GCI［2，1］有较小的网格相关性；因此本模型选取中等网格密度。入口边界平均流速和湍流强度抛物线如图4所示。出口采用出口（OUTLET）类型，区域侧面采用壁面（WALL）边界条件，计算区域顶部采用对称边界（Symmetry）条件。

图1 风洞试验图

图2 不同位置测点分布图

采用LES模型时，绝大部分近壁区满足y+≈1的要求，网格数为300×200×120，入口边界采用高斯概率密度分布公式来生成瞬时脉动速度，如式（9）所示

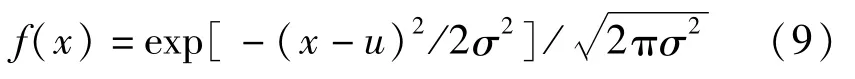
式中:σ为在入口边界不同高度处的湍流强度，%。时间步长设定为0.0005 s，满足绝大部分计算区域Courant-Friedrichs-Levy（CFL）值低于1的要求。

图3 计算模型图

图4 入口边界沿建筑高度方向变化的速度和湍流强度分布图（a）速度；（b）湍流强度

2.4 计算结果对比分析

在相同计算工况和同等计算机配置条件下，三种湍流模型所消耗的计算时间比为:Zero-EQ: MMK:LES＝1:1.6:15，很显然，Zero-EQ能够比MMK湍流模型快60%，是LES模型计算所需时间的1／15。计算三个湍流模型预测结果与风洞实验数据的平均相对误差，分别得到12.9%、7.9%和11.8%（MMK，LES和Zero-EQ），可以看出Zero-EQ模型具有一定的优势。因此，Zero-EQ模型能够比较快速地模拟建筑群周围的流场分布，同时Zero-EQ模型能相对准确地预测流场速度大小分布。

文章仅考虑了Y4横行中的四个测点X2Y4，X4Y4，X5Y4和X8Y4的纵向分速度分布，更多横行对比分析可参考文献［17］。因Y4行位于多栋建筑的中心位置，该行测点的对比分析能够有效地评估Zero-EQ模型的优劣。图5为各测点的MMK、LES、Zero-EQ的模拟结果与风洞实验数据对比，在纵向分速度上，三个模型皆能准确地预测测点X2Y4的速度，但Zero-EQ能更准确地预测建筑顶部区域的漩涡。在测点X4Y4，MMK和LES虽能预测流场分布的趋势，但其速度大小较风洞实验数值偏小，而Zero-EQ虽与实验数据误差较小，却不能有效捕捉流场分布；在测点X5Y4，三个模型的预测结果与风洞实验数据吻合较好；在测点X8Y4，MMK和LES模型的预测速度与实验结果相比偏小，而Zero-EQ虽不能完全地预测出建筑背风面区域流场的涡旋分布，但能有效地预测此区域的速度大小。

从风洞实验数据及MMK和LES模型预测结果对比，可以看出湍流模型能相对准确地预测流场速度大小的分布，但不能完全地预测建筑扰流场的流动趋势，这是由于（1）现有的湍流模型仍不能准确地描述非近壁区的转捩流动以及非稳态流动中的漩涡脱落；（2）风洞试验采用的热线风速仪不能完全准确地捕捉非稳态流动漩涡区域的复杂流动，这是试验的不足之处，今后将采用更精确的实验设备。但总的说来，通过验证和分析，相比MMK和LES模型，Zero-EQ能够快速而又相对有效地模拟不规则建筑群的流场分布。

3 零方程湍流模型应用研究

3.1 低碳生态建设专项规划介绍

文章选择成都市蒲江县寿安镇生态建设项目，来探讨零方程湍流模型应用于实际工程项目的可行性。结合寿安镇当地气象条件，建立较准确的城市三维模型，分析城区各区域风热环境的特点，提出寿安新城的城市规划建议，达到工程应用的目的。

虽然寿安镇旧城区作为一个小区域，但其仍满足城市地形区域UTZ（Urban Terrain Zone）的部分分类特点［18］，即:镇中心商业区（UTZ-1）、寿安中学校区（UTZ-2）、高层楼居民生活区（UTZ-5）和镇郊居民区（UTZ-6）。其各自详细的建筑信息见表1和如图6所示。

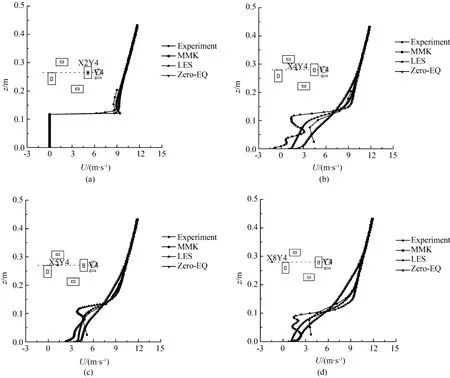
图5 不同测点纵向速度（U）沿建筑高度方向（Z坐标）变化的分布图

表1 寿安旧城区不同区域的特点

3.2 模拟设定

根据近30多年浦江县的气象资料，年平均风速为0.9 m／s，年静风频率超过40%，空气水平扩散条件差，全年主导风向为NNE，年平均气温为16.5℃。建立寿安镇准确的城区建筑模型，分别设定计算区域入口边界、太阳辐射模型和壁面边界条件:“WIND”入口条件，考虑太阳辐射对地面的影响，Tin＝25℃，选择夏季6月23日正午时分，入口速度选择对数函数分布轮廓线，U10＝0.9 m／s；建筑群表面设置温度边界条件T＝30℃，表面粗糙度为0.005 m；计算区域网格为600×500×120，满足绝大部分壁面无量纲数y+＜300。

3.3 结果分析

根据四个不同地形区域建筑分布的特点，分析区域内风热环境的分布，可供建筑师和工程师做规划设计时参考。区域内速度大小和温度分布图分别如图7、8所示，分布图高度选择行人的肩膀至头部位置处，大约为1.5 m。分析如下:

（1）镇中心商业区（UTZ-1）由于商业区位于城镇中心，街道普遍较窄（约7 m），受周围较高建筑的影响大，由图7可知，区域内的速度值普遍偏低，低于0.20 m／s；而街区内温度较高，如图8所示，高于35°C，部分位置温度甚至超过40°C。很显然，在街区通风不畅、太阳辐射比较强烈的情况下，街区内的热环境舒适度比较差，行人普遍感到不舒适；受此影响，城市热岛现象比较严重，区域内温度整体偏高，使得商业区的建筑能耗增大。

图6 寿安旧城区建筑模型和区域分类图

（2）寿安中学校区（UTZ-2）在寿安中学校区内，因学生操场位置周围无高层建筑，操场内风速大小受周围环境影响较小，与城镇近郊的风速相近，最高达到0.45 m／s；学生教学楼和教师办公楼周围流场风速较镇中心商业区高，风环境舒适度较好，受其影响，此区域温度大多维持在28～32°C之间，最高不超过36°C，热环境舒适度基本可以接受。

图7 寿安旧城区速度大小分布图在1.5 m处

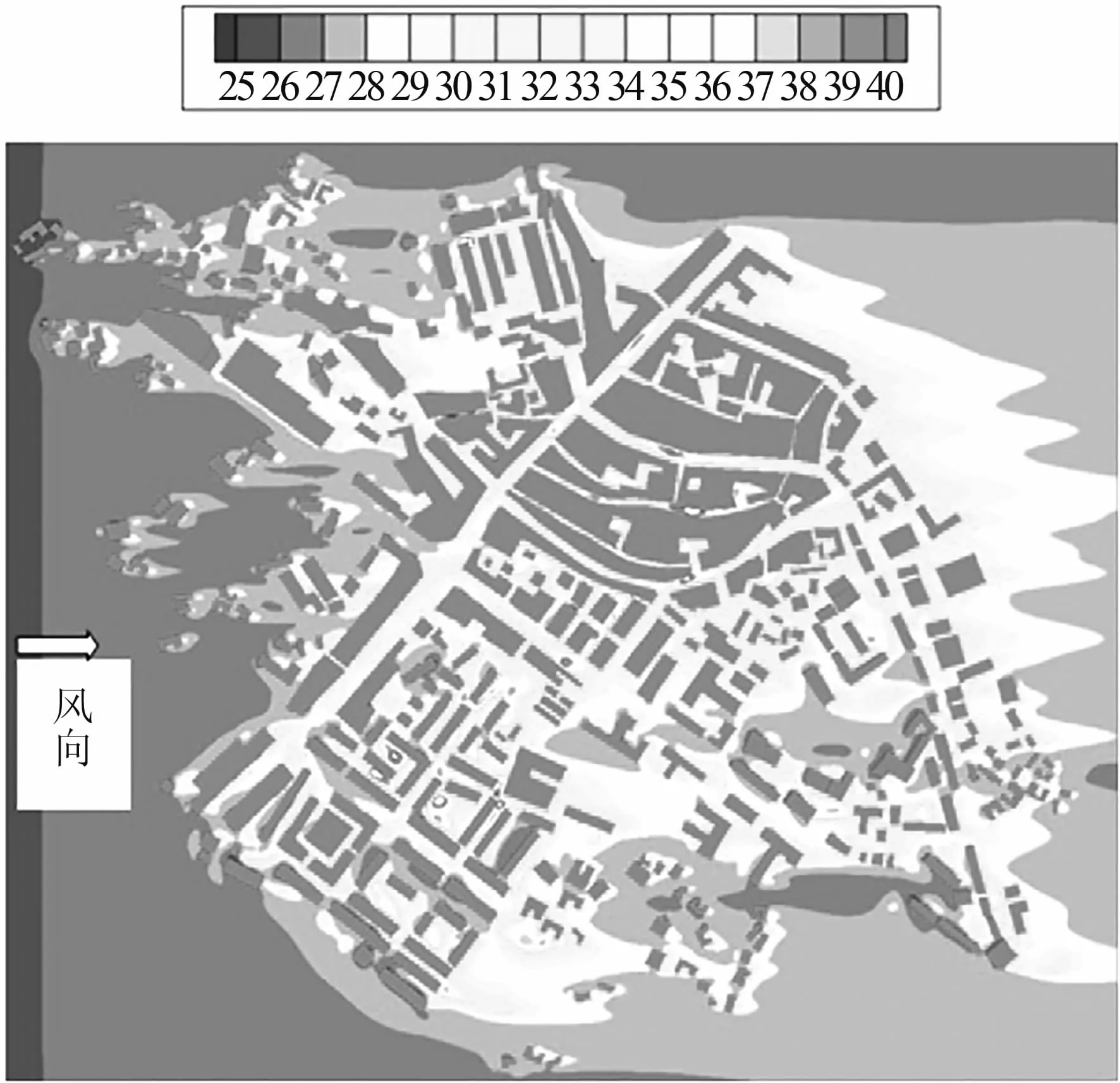
图8 寿安旧城区温度分布图在1.5 m处

（3）高层楼居民生活区（UTZ-5）在高层楼居民区，由于其远离镇中心，且在主导风向上游区域，风环境比镇中心商业区稍好，但由于大多数的高层住宅楼选用“口”字型设计，使得几栋楼中心区域的风速偏低，普遍低于0.1 m／s，风环境舒适度较差；相应地，高层楼居民区内的温度偏高，维持在35°C以上，最高可达43°C，行人区域的热环境较差。

（4）镇郊居民区（UTZ-6）在城镇近郊，居民房屋大多呈单栋位置分布，房屋之间的间距较大，且房屋高度一般在4～7 m之间，遮蔽效应不明显，因此居民区周围的风环境较好（大约0.4 m／s），热环境舒适度较好，温度普遍维持在30°C上下。

通过对寿安镇旧城区不同地形区域风热环境分析，对新城区城市规划提供如下建议:

（1）有必要通过合理规划商业区的布局，采取增大街区宽度，加大绿化、水体建设等措施来减少城市热岛效应的影响；同时，根据当地盛行风向和风速大小，选择偏南北走向的街道布局，加强城镇建筑间通风。

（2）受当地风速偏低的影响，严格规划城镇高层居民区布局设计，杜绝“口”字型分布设计，合理控制建筑群的密度，保证行人区域内风环境舒适性要求；

（3）建议今后在新城规划设计时，对不同建筑规划设计方案建立CFD建筑模型，分析其受当地气象条件影响的微气候环境，提供给建筑师和工程师足够准确的信息。

4 结论

通过上述研究可知:

（1）Zero-EQ模型虽不能完全预测建筑扰流的流动趋势，但能相对准确地预测流场速度分布；在同等计算机配置下，Zero-EQ模型比MMK模型快60%，是LES模型计算所需时间的1／15，能快速且相对有效地预测不规则建筑群的风环境分布。

（2）通过分析不同地形区域的风热环境特点，Zero-EQ模型能够快速地预测城镇微气候环境，可供建筑师和工程师做城市规划和生态环境设计时参考，达到实际工程应用的目的。

（3）建议今后城镇低碳社区在建设过程中，选用CFD模拟技术对新建或改建建筑周围微气候环境进行预测，优化和改善城镇微气候环境状况。

文章的零方程湍流模型是基于缩尺风洞试验得到的，而此风洞试验未考虑强浮力流动效应等影响，今后将继续研究零湍流模型中自然对流引起的浮力流动对建筑扰流的影响，同时将对城镇社区尺度下的微气候环境进行现场实测，验证零方程湍流模型的准确性。

［1］ 关吉平，任鹏杰，周成，等.高层建筑行人高度风环境风洞试验研究［J］.山东建筑大学学报，2010，25（1）:21-25.

［2］ 闫整，房文娟，肖华斌.上海低碳生态城市的规划实践进展［J］.山东建筑大学学报，2011，26（3）:266-270.

［3］ 牛盛楠，张欣宜，黄成，等.天津地区居住区采光宇室外风环境模拟研究［J］.山东建筑大学学报，2013，28（1）:12-17.

［4］ Murakami S.，Ooka R.，Mochida A.，et al.CFD analysis of wind climate from human scale to urban scale［J］.Journal ofWind Engineering and Industrial Aerodynamics，1999，81:57-81.

［5］ Chen Q.，Xu W..A zero-equation turbulence model for indoor airflow simulation［J］.Energy Buildings，1998，28（2）:137-144.

［6］ Zhai Z.Q.，Chen Q.Y.，Haves P.，et al.On approaches to couple energy simulation and computational fluid dynamics programs［J］.Build Environment，2002，37（8-9）:857-864.

［7］ Srebric J.，Chen Q.Y.，Glicksman L..Validation of a zeroequation turbulence model for complex indoor airflow simulaiton［J］.ASHRAE Transactions，1999，105（2）:414-427.

［8］ Qian Y..Development of algebraic turbulence model for airflow and contaminant simulations around building［D］.University Park:The Pennsylvania State University，2004.

［9］ Van Driest E.R..On turbulent flow near a wall［J］.Journal of Aero Science，1956，23（1）:1007-1010.

［10］Cebeci T.，Smith A..Analysis of turbulence boundary layers，series in applied mathematics and methods:XV［M］.University Park:Academic Press，1974.

［11］Baldwin B.S.，Lomax H..Thin-layer approximation and algebraic models for separated turbulence flows［J］.AIAA Paper，1978，278-286.

［12］Davidovic D..Improvements in numerical airflow modeling around multiple buidlings［D］.University Park:The Pennsylvania State University，2009.

［13］Tsuchiya M.，Murakami S.，Mochida A.，et al.Development of a new kappa-epsilonmodel for flow and pressure fieldsaround bluff body［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，67-68（1）:169-182.

［14］Kato M.，Launder B.E..Themodeling of turbulent flow around stationary and vibrating square cylinders［J］.Preprints of 9th Symposium on Turbulent Shear Flow，1993，10（4）:1-6.

［15］Tominaga Y.，Mochida A.，Yoshie R.，et al.AIJguidelines for practical applications of CFD to pedestrian wind environment around buildings［J］.Journal ofWind Engineering and Industrial Aerodynamics，2008，96（10-11）:1749-1761.

［16］Davidovic D.，Liu J.，Heidarinejad M.，etal.Airflow study for a cluster of campus buildings using different turbulence modeling approaches［J］.Invited Paper for the Third Issue of International Journal in Building，Urban，Interior and Landscape Technology，2014.

［17］刘吉营.基于零方程湍流模型的非等温城市区域热环境的模拟研究［D］.成都:西南交通大学，2013.

［18］Ellefsen R..Current assessmentof Building Construction Types in Worldwide Example Cities［M］.Dahlgren:Naval Surface Warfare Center Dahlgren Division，1999.

（责任编辑：吴芹）

Numerical simulation of them icro climate urban environment using a zero-equation turbulencemodel

Liu Jiying1，2，3，*，Guo Min1，2，3，Srebric Jelena4，et al.

（1.School of Thermal Engineering，Shandong Jianzhu University，Jinan 250101，China；2.Shandong Key Laboratory of Building Energy Saving Technologies，Shandong Jianzhu University，Jinan 250101，China；3.Shandong Key Laboratory of Renewable Energy Utilization Technologies in Building，Shandong Jianzhu University，Jinan 250101，China；4.Department of Mechanical Engineering，University of Maryland，University Park 20742，USA）

The micro climate urban environment has an important effect on outdoor residential environment and building energy consumption.Numerical simulation as a fast prediction method can effectively evaluate the quality of neighborhood planning.In this paper，a rapid and relatively reliable Zero-equation turbulencemodel（Zero-EQ）is provided through analyzing and improvingmeasurement data of the wind tunnel experiment，and compared with two-equation turbulence model（MMK），Large Eddy Simulation（LES）and a wind tunnel experiment.By investigating the application of Zero-EQmodel in Shouan Town，this research discusses the feasibility of themodel's application to the real project.The result shows that the computational speed of Zero-EQmodel is faster by 60%than MMK model，and only 1／15 of thatusing LESmodel under the same computational resources，indicating the capability of Zero-EQ on relatively accurately predicting the wind flow field in a complex neighborhood.In the end，Zero-EQ can quickly predict the micro climate urban environment and provide reasonable suggestion for the urban planning and design by means of studying the wind and thermal environment over different urban terrains.

TU375.1

A

1673-7644（2014）06-0512-08

2014-10-31

国家科技支撑计划子课题项目（2012BAJ06B03-01）；山东建筑大学博士科研基金项目（XNBS1408）

刘吉营（1983-），男，讲师，博士，主要从事城市热环境和绿色建筑等方面的研究.E-mail:jxl83＠sdjzu.edu.cn