双调和型映照的Landau定理

石擎天，黄心中

（华侨大学数学科学学院，福建泉州362021）

双调和型映照的Landau定理

石擎天，黄心中

（华侨大学数学科学学院，福建泉州362021）

利用单位圆盘上有界调和映照的系数估计及Schwarz引理，对双调和映照F（z）及其在微分算子L作用下LF（z）的Landau定理中的单叶半径进行估计.所得结果改进了刘名生等和Chen等的研究结果.

双调和型映照；Landau定理；微分算子；Schwarz引理

1 预备知识

关于平面单连通区域上有界调和映照，有如下估计不等式.

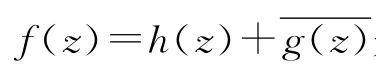
其中，n＝2，3，….应用上述结果，文献［5］证明了

定理C［5］设F（z）＝｜z｜2G（z）＋K（z）是单位圆盘D上双调和映照，G（z）和K（z）在D上调和，满足F（0）＝K（0）＝0且JF（0）＝1，｜G（z）｜≤M，｜K（z）｜≤M，z∈D则存在常数ρ1∈（0，1），使得F（z）在圆盘Dρ1上单叶且F（Dρ1）包含单叶圆盘Dσ1.ρ1是方程

事实上，定理C要求满足G（0）＝0，否则得到的σ1将会得到变化.文献［8－9］对算子L作用于双调和映照的Landau定理进行估计，得到如下结论.

定理D［9］假设F（z）＝｜z｜2G（z）＋K（z）是单位圆盘D上的双调和映照，G（z）和K（z）在D上调和，满足F（0）＝K（0）＝JF（0）－1＝0，且｜G（z）｜≤M，｜K（z）｜≤M，M≥1.则存在常数ρ∈（0，1），使得LF（z）在圆盘Dρ上单叶且LF（Dρ）包含单叶圆盘Dσ.其中ρ是方程

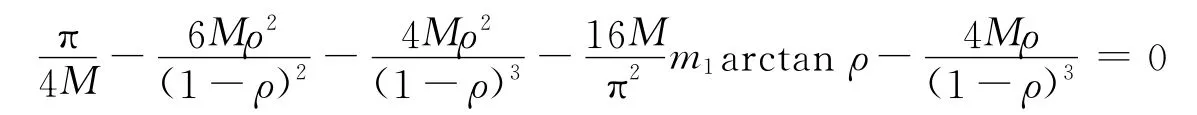
最近，Chen等在文献［10］中改进了上述定理，当p＝2时有如下结论.

定理E设F（z）＝｜z｜2G（z）＋K（z）是D上双调和映照，其中G（z）和K（z）是D上调和映照，满足F（0）＝K（0）＝JF（0）－1＝0且｜G（z）｜≤M，｜K（z）｜≤M，M≥1.则存在常数ρ2∈（0，1），使得LF（z）在圆盘Dρ2上单叶且LF（Dρ2）包含单叶圆盘Dσ2.这里ρ2是方程

定理F设F（z）＝｜z｜2G（z）是D上双调和映照，G（z）是D上调和映照，满足G（0）＝JG（0）－1＝0且｜G（z）｜≤M，z∈D.则LF（z）在Dρ3上单叶且LF（Dρ3）包含单叶圆盘Dσ3.其中ρ3是方程

2 主要结果及其证明

针对定理C，证明如下.

定理1设F（z）＝｜z｜2G（z）＋K（z）是单位圆盘D上的双调和映照，G（z）和K（z）在D上调和，满足F（0）＝G（0）＝K（0）＝JF（0）－1＝0且｜G（z）｜≤M，｜K（z）｜≤M，M≥1.则存在常数r1∈（0，1），使得F（z）在圆盘Dr1上单叶且F（Dr1）包含单叶圆盘DR1.这里r1是方程

K0

给定r∈（0，1），任取z1，z2∈D，且z1≠z2，［z1，z2］表示连接z1，z2的直线段.

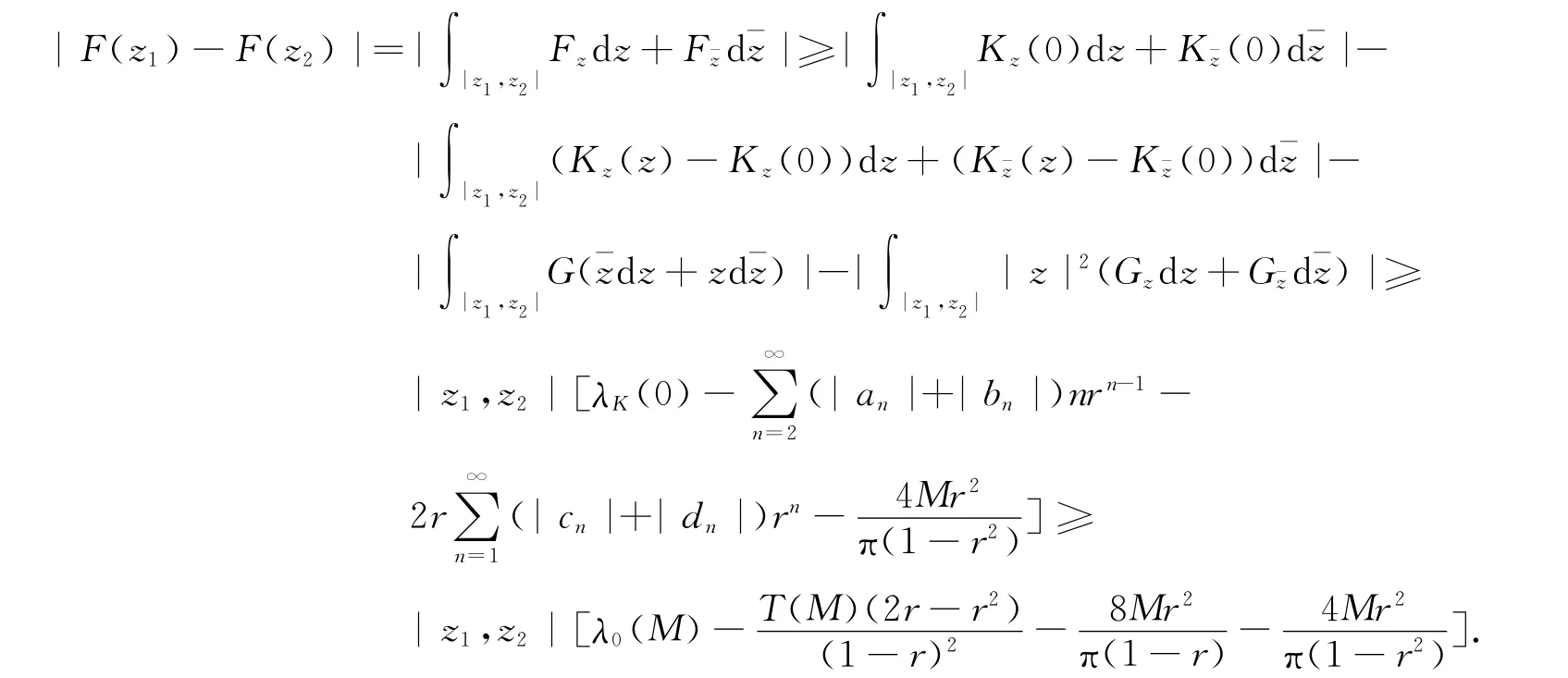
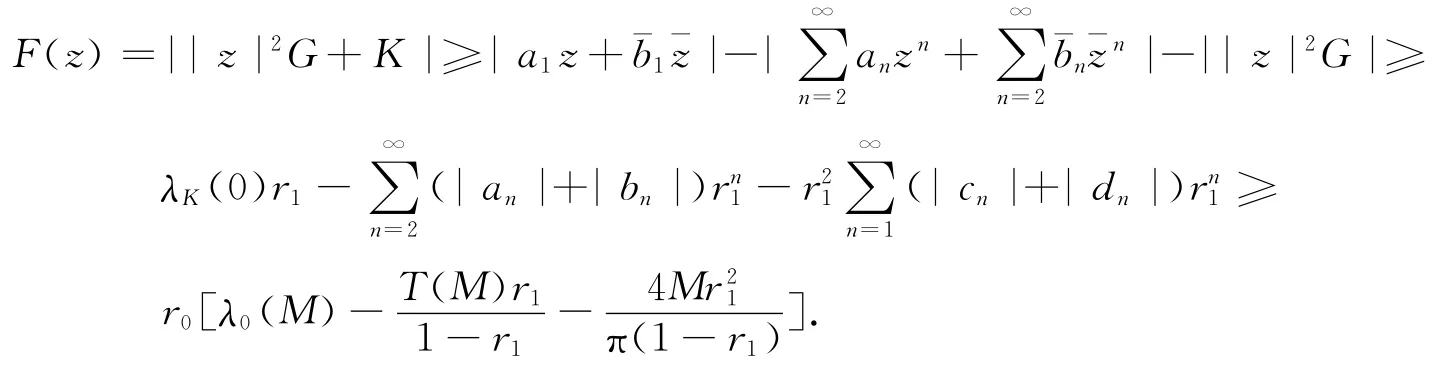
通过Matlab软件计算，比较定理1与定理C，如表1所示.

表1 定理1与定理C的比较Tab.1 Compare theorem 1with theorem C

下面研究微分算子L作用于双调和映照的Landau定理问题.

定理2设F（z）＝｜z｜2G（z）＋K（z）是单位圆盘D上双调和映照，G（z）和K（z）是D上调和映照，满足F（0）＝K（0）＝JF（0）－1＝0且｜G（z）｜≤M，｜K（z）｜≤M，M≥1.则LF（z）在Dr2上单叶且LF（Dr2）包含单叶圆盘DR2.其中r2是方程

给定r∈（0，1），任取z1，z2∈D且z1≠z2，［z1，z2］表示连接z1，z2的直线段，则有

故定理得证.

通过Matlab软件计算，比较定理2和定理E，如表2所示.

表2 定理2与定理E的比较Tab.2 Compare theorem 2with theorem E

作为应用，考虑定理2中K≡0的情形，得到了如下结论.

定理3设F（z）＝｜z｜2G（z）是单位圆盘D上的双调和映照，G（z）是D上调和映照，满足G（0）＝JG（0）－1＝0，且｜G（z）｜≤M，M≥1.则LF（z）在Dr3上单叶，且LF（Dr3）包含单叶圆盘DR3.其中，r3是方程

通过Matlab软件计算，比较定理3和定理F，如表3所示.

表3 定理3与定理F的比较Tab.3 Compare theorem 3with theorem F

3 结束语

以上研究方法表明：充分应用调和映照的Schwarz引理和系数估计不等式可以得到更好的结果，在对数调和映照类、有界多重调和函数的相应问题的估计也可以得到进一步的结果.

［1］ LEWY H.On the non－vanishing of the Jacobian in certain one－to－one mappings［J］.Bull Amer Math Soc，1936，42（10）：689－692.

［2］ ABDULHADI Z，MUHANNA Y，KHURI S.On univalent solutions of the biharmonic equations［J］.Journal of Inequalities Applications，2005（5）：469－478.

［3］ ABDULHADI Z，MUHANNA Y，KHURI S.On some properties of solutions of the biharmonic equation［J］.Applied Mathematics and Computation，2006，177（1）：346－351.

［4］ LIU Ming－sheng，LIU Zhi－wen.On bloch constants for certain harmonic mappings［J］.Southeast Asian Bulletin of Mathematics，2012，36（3）：1－10.

［5］ 刘名生，刘志文，朱玉灿.某类双调和映射的Landau型定理［J］.数学学报，2011，54（1）：69－80.

［6］ COLONNA F.The Bloch constant of bounded harmonic mappings［J］.Indiana Univ Math J，1989，38：829－840.

［7］ LIU Ming－sheng.Landau theorem for planar harmonic mappings［J］.Comput Math Appl，2009，57（7）：1142－1126.

［8］ 夏小青，黄心中.一类双调和映照的单叶半径估计［J］.华侨大学学报：自然科学版，2011，32（2）：218－221.

［9］ CHEN S，PONNUSAM S，WANG X.Landau theorem for certain biharmonic mappings［J］.Applied Mathematics and Computation，2009，208（2）：427－433.

［10］ CHEN S，PONNUSAM S，WANG X.On properties of solutions of the p－harmonic equation［EB／OL］.（2012－04－12）［2012－09－30］.http：／／arxiv.org／pdf／1204.2767.pdf.

［11］ 夏小青，黄心中.平面有界调和函数的Bloch常数估计［J］.数学年刊，2010，31A（6）：769－776.

Landau′s Theorem for Biharmonic－Type Mappings

SHI Qing－tian，HUANG Xin－zhong
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

Using the coefficient inequalities for bounded harmonic mappings on the unit disk and Schwarz lemma，Landau′s theorems for biharmonic mappings F（z）and LF（z），where Lis a differential operator，are considered.Our results improve the latest one made by Liu Ming－sheng and Chen.

biharmonic－type mapping；Landau′s theorem；differential operator；Schwarz lemma

O 174.51；O 174.55

A

（责任编辑：黄晓楠 英文审校：黄心中）

1000－5013（2014）01－0102－05

10.11830／ISSN.1000－5013.2014.01.0102

2012－10－23

黄心中（1957－），男，教授，主要从事函数论的研究.E－mail：huangxz＠hqu.edu.cn.

福建省自然科学基金资助项目（2011J0101）