一种联图的Cordial性
倪臣敏,刘峙山,卢福良
(1.华侨大学厦门工学院高等数学教学系,福建厦门361021;2.仰恩大学数学系,福建泉州362014;3.临沂大学数学系,山东临沂276005)
一种联图的Cordial性
倪臣敏1,刘峙山2,卢福良3
(1.华侨大学厦门工学院高等数学教学系,福建厦门361021;2.仰恩大学数学系,福建泉州362014;3.临沂大学数学系,山东临沂276005)
引入第一类图G的概念,即若存在一个标号f,使得|v0(G)-v1(G)|≤1,e0(G)≥e1(G),则称G为第一类图.证明了第一类图G与路P的联图G∨P,当P的阶数大于等于G的最大度的2倍加2,即|P|≥2Δ(G)+2时,都是Cordial图,并进一步给出图G是第一类图的两个充分条件.
第一类图;路;联;Cordial图
自1987年Cahit提出Cordial图的概念[1]至今,各种图的Cordial性的研究不断出现[110],如有关联图的Cordial性的结果研究[2-5].Cm∨Kn,mCn,Pm∨Kn,Pm∨K1,n的Cordial性已在一定条件下得到解决,但Cm,Kn,Pm,Kn都是十分具体的,简单的图.文献[3]研究由G导出的图Pt(G)(即把G的所有边都用长为t的路来代替后得到的新图)的Cordial性,但有关结论都是在G是Cordial图的前提条件下给出的;文献[4]给出了Pt(K2n),Pt(K2n+1)的Cordial性证明结论.但有关联图G∨P的Cordial性均未作深入的研究.本文引入了第一类图的概念,证明了这类图中的任意一个图G,只要路P的阶数|P|≥2Δ(G)+2,G∨P就是Cordial图.
1 相关定义
文中均为无向有限的简单图,标号为0-1标号.对于图G的顶点集合V(G)的标号f,以f(u,v)=|f(u)-f(v)|导出G的边集合E(G)的标号.记

并以v0,v1,e0,e1分别表示它们的基数.
当同一图G有更细的标号时,引入更细的标号,如用v0(f)=v0(f;G),表示图G中标号f为0的顶点集合的基数.
文中标i的顶点或者边简称为i点或者i边,其中i=0,1.
定义1[11]设G和H是两个不相交的图,称G∨H为G和H的联图.其中,V(G∨H)=V(G)∪V(H),E(G∨H)=E(G)∪E(H)∪{uv|u∈V(G),v∈V(H)}.
定义2[1]如果对于图G,存在一个标号f,使得
1)|v0(G)-v1(G)|≤1;
2)|e0(G)-e1(G)|≤1.
则称G为Cordial图,f是G的Cordial标号.
2 主要结果及其证明

引理1设f是图G的一个标号,x∈V(G),g是仅把顶点x的f标号改变后得到的图G的标号,则有

证明 因为d1(f;x)=d0(f;x),又g与f导出的边标号恰好只对于与顶点x关联的边不同,所以有
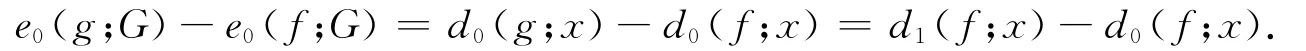
证毕.
引理2设f是图G的一个标号,{x,y}⊂V(G),且f(x)≠f(y),g是仅对换x,y的f标号后得到的G的标号,则有v0(f)=v0(g)且有
1)当xy∉E(G)时,有
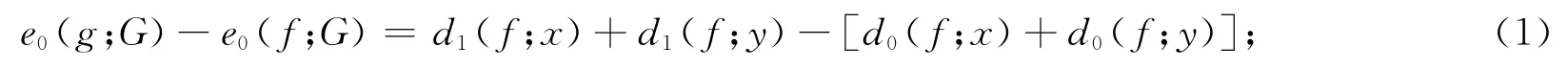
2)当xy∈E(G)时,有

证明 由G的定义可知,显然有v0(f)=v0(g),则
1)对换x,y的标号相当于先改变x标号,再改变y的标号,由引理1可得,式(1)成立;
2)与1)的情况比较可得,改变x标号时,边xy由1边变成0边,故式(2)中的d1(f;y)比式(1)中的d1(f;y)少1,而式(2)中的d0(f;y)比式(1)中的d0(f;y)大1.因此,式(2)的右端比式(1)的右端少2,故可得等式(2).
定义3若图G存在一个标号f,使得
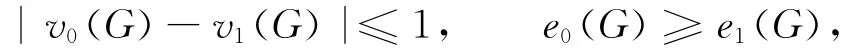
则称G为第一类图;否则,称G为第二类图.
引理3若G为第一类图,则G或有标号h,使得

或有标号g,使得

证明 因G为第一类图,故有标号f,使得
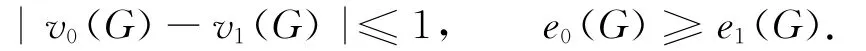
当e0(G)=e1(G)时,f即引理的h,故可设e0(G)>e1(G).分两种情况进行讨论.
1)当|G|是奇数时,令V(G)={x1,x2,…,xl;y1,y2,…,yl;z},f(xi)=f(z)=0,f(yi)=1,i=1,…,l,则有

若d0(z)>d1(z),改变z的标号,可得v0=v1-1,由引理1知,e0(G)减少,但减少量不超过Δ(G).若d0(z)≤d1(z),则存在某个i,使得d0(xi)+d0(yi)-d1(xi)-d1(yi)>0.对换xi,yi的标号,由引理2可知,e0(G)减少,且当xiyi∉E(G)时,e0(G)的减少量为d0(xi)+d0(yi)-d1(xi)-d1(yi)≤d0(xi)+d0(yi)≤2Δ(G);且当xiyi∈E(G)时,因xi,yi的标号不同,故d1(xi)≥1,d1(yi)≥1,d1(xi)+d1(yi)≥2.由引理2可知:e0(G)的减少量为d0(xi)+d0(yi)+2-d1(xi)-d1(yi)≤d0(xi)+d0(yi)≤2Δ(G);若e0(G)变小后,仍有e0(G)>e1(G),可再继续上面的步骤,直到出现e0(G)≤e1(G)为止.
令最后保持e0(G)>e1(G)的标号为h,出现e0(G)≤e1(G)的标号为g,则有e0(h;G)>e1(h;G),e0(g;G)≤e1(g;G).因e0(G)+e1(G)=e(G),故有e1(g;G)≤e(G)/2<e0(h;G).在每对换一对顶点的标号时,e0(G)的减少量不超过2Δ(G),即e0(h;G)-e0(h;G)≤2Δ(G),从而易得引理3的两个不等式.
对换xi,yi的标号并不影响G中0点和1点的数目,所以有
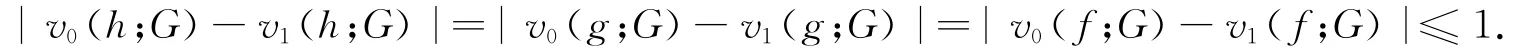
2)当|G|是偶数时,不出现上面的z,保留前面关于xi,yi的标号变化时的证明即可证.
引理4设f是n阶路P=Pu1,…,un的一个标号(其中n≥4),|E0,0(P)|>0,|E1,1(P)|>0,则P存在另一标号g,满足v0(g)=v1(f),e0(g)=e1(f)-2.
证明 不妨设f(ui)=f(ui+1)=0,f(uj)=f(uj+1)=1,其中i+1<j,i=1,2,…,n-3,并设ui+1与uj之间无0边.那么,必有f(ui+2)=1,f(ui+3)=0,f(ui+4)=1,…,f(uj-1)=0.
对换ui+1与ui+2的标号,v0(P)和e0(P)并不改变,但是新的0边ui+2ui+3与0边ujuj+1的距离变小.用此方法变换直到uj-2uj-1的标号为0,此时,再对换uj-1和uj的标号,即得所需标号g.
引理5对于任意的n阶路P=Pu1,…,un(其中n≥3)及K={0,1,2,…,n-2},都存在标号f,使得


定理1若G*为第一类图,G=G*∨P,|P|≥2Δ(G)+2,则G是Cordial图.
证明 由题意可知,把G*视为引理3中的G,因为G*与P中顶点标号0,1可以独立选择,因此利用引理3,5的标号,使得|v0(G)-v1(G)|≤1.再有,对G的任意边标号,均有e0(G)+e1(G)=e(G),故Cordial图的边标号条件|e0(G)-e1(G)|≤1等价于|e0(G)-e(G)/2|≤1/2.因为G*是第一类图,根据引理3可分如下两种情况讨论.
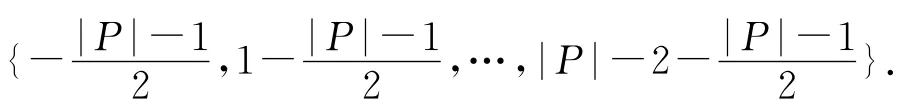
情形2G*有标号g,使得e(G*)/2-Δ(G*)≤e0(g;G*)≤e(G*)/2.令e0(g;G*)=e(G*)/2+β,其中-Δ(G*)≤β≤0.故只需选择P的标号,使得e0(P)-e(P)/2取值-β或-β±1/2即可.由于有|P|-2-(|P|-1)/2=(|P|-3)/2≥Δ(G*)-1/2≥-β-1/2,故e0(P)-e(P)/2必然可以取到-β或-β±1/2.
3 第一类图的充分条件及其证明
定理21)若奇阶图G的V(G)={x1,x2,…,xk,y1,y2,…,yk,z}满足xiyi∉E(G),i=1,2,…,k,则G为第一类图.
2)若偶阶图G的V(G)={x1,x2,…,xk,y1,y2,…,yk}满足xiyi∉E(G),i=1,2,…,k,则G为第一类图.
证明 1)给G一个标号f,使得f(xi)=f(z)=0,f(yi)=1,i=1,2,…,k.若e0(f;G)≥e1(f;G),则G即为第一类图.

当d1(z)>d0(z)>0时,改变z的标号,e0(G)变大,则当某个i使得d1(xi)+d1(yi)-d0(xi)-d0(yi)>0时,由引理2的式(1)可知,对换xi,yi的标号,e0(G)增加.将此步骤进行若干次,必能得到一种标号,使得e0(G)≥e1(G).命题得证.
2)证明方法与1)的方法类似,在此略过.
定理3如果Δ(G)≤|G|/2-1,则G为第一类图.
证明 考虑G的补图¯G,由已知条件知δ(G)≥|G|/2.由Dirac定理知,¯G有Hamilton圈H,在H中相邻的每对顶点在G中不相邻,故G满足定理2的条件,从而G为第一类图.
若e0(f;G)<e1(f;G),则有
[1] CAHIT I.Cordial graghs:A weak version of graceful and harmonious graphs[J].Ars Combin,1987(23):201-208.
[2] JOSEPH A G.A dynamic survey of graph labeling[J].Electronic Journal of Combinatorics,2009(16):49-53.
[3] ANDAR M,BOXWALA S,LIMAYE N B.On the cordiality of the t-uniform homeomorphs-I[J].Ars Combin,2003(66):313-318.
[4] ANDAR M,BOXWALA S,LIMAYE N B.On the cordiality of the t-uniform homeomorphs-II[J].Ars Combin,2003(67):213-220.
[5] 倪臣敏,刘峙山,陈丽娜.关于一点联的Cordial性的一个结果的推广[J].延边大学学报:自然科学版,2007,33(2):94-97.
[6] XIE Yan-tao,CHE Ying-tao,LIU Zhi-shan.The cordiality on the union of 3-regular connected graph and cycle[J].Chinese Quarterly Journal of Mathematics,2010,25(2):244-248.
[7] 刘群,刘峙山.最大边数的Cordial图的构造[J].数学研究,2003,36(4):437-439.
[8] 刘峙山,堵根民.三正则连通图的Cordial性[J].数学研究,2007,40(1):114-116.
[9] GHEBLEH M,KHOEILAR R.A note on“H-cordial graphs”[J].Bull Inst Combin Appl,2001(31):60-68.
[10] KIRCHHERR W W.NEPS operations on cordial graphs[J].Discrete Math,1993(115):201-209.
[11] BONDY J A,MURTY U S R.Graph theory with applications[M].New York:American Elsevier,1976:117-118.
On the Cordiality of a Union of Graphs
NI Chen-min1,LIU Zhi-shan2,LU Fu-liang3
(1.Teaching Department of High Mathematics of Institue of Technology,Huaqiao University,Xiamen 361021,China;2.Department of Mathematics,Yangen Universiyty,Quanzhou 362014,China;3.Department of Mathematics,Linyi Universiyty,Linyi 276005,China)
The first class of graphs is introduced.If a graph has a lebaling f,s.t.|v0(G)-v1(G)|≤1,e0(G)≥e1(G),it is called to be the first class of graphs.Let Gbe a graph of this class and Pbe a path with|P|≥2Δ(G)+2,it is proved that G∨Pis a Cordial graph,and two sufficient conditions are given to make Gto be the first class of graphs.
the first class of graphs;path;union;cordial graph
O 157.5
A
(责任编辑:陈志贤 英文审校:黄心中)
1000-5013(2014)01-0117-04
10.11830/ISSN.1000-5013.2014.01.0117
2012-12-19
倪臣敏(1980-),女,讲师,主要从事图论与组合学,图像处理与分析的研究.E-mail:cmni@163.com.
国家自然科学基金资助项目(11226288)
——丘成桐

