公平神经网络的未知信源数盲分离算法

李凯，李慧，王启志

（1.华侨大学机电及自动化学院，福建厦门361021；

2.中国人民解放军理工大学通信工程学院，江苏南京210007）

公平神经网络的未知信源数盲分离算法

李凯1，李慧2，王启志1

（1.华侨大学机电及自动化学院，福建厦门361021；

2.中国人民解放军理工大学通信工程学院，江苏南京210007）

提出一种基于公平神经网络的学习算法.设置一个合理的信源数初始值，通过构造的一个稳定性判决器，能够自适应调整神经网络的维数，并估计出信源数真实值，从而使信源得以成功分离.理论分析表明，在其数学统计意义上缩减了训练时间；而计算机仿真结果表明，在其不同信源数条件下均能快速收敛.

超定盲分离；信源数；自适应神经网络；稳定性判决器

盲源分离（BSS）是指源信号和传输信道参数均未知的情况下，根据源信号的统计特性，仅由观测信号来恢复或分离出源信号的过程.近年来，BSS已成为信号处理和神经网络领域的研究热点，在数据通信［1］、语音识别、图像恢复、生物医学和故障检测［2］等诸多领域都有广泛应用.虽然BSS的研究成果已经相当丰硕，但大多数相关文献都假定信源数已知，然而实际应用中信源数通常是未知的，所以研究未知信源数条件下的盲分离更具现实意义.独立源数目未知的盲分离，主要研究的是超定条件下（接收天线数M大于信源数N）基于神经网络的学习算法［3－8］.1999年，Cichocki等［3］采用自然梯度算法和M× N维解混矩阵仿真实验表明：在收敛阶段，网络输出由N个源信号的拷贝和M－N个冗余分量构成，容易导致算法发散.冶继民等［］分析认为，解混矩阵在某一等价类中的冗余移动是算法不能稳定收敛的原因，并提出利用正交投影来消除引起冗余移动的冗余分量.然而，Sun等［］却巧妙地利用这种冗余分量造成的权值矩阵梯度振荡来构造一个稳定性判决器，从而在分离算法的学习过程中，不断地调整神经网络维数（即信源数估计值），使其逼近真实值，最终~N＝N.文献［5－6］分别假定初始化阶段的取值为最大值和最小值，即~N＝M和~N＝2，然而从数学角度来看，这种初始值的设置并不合理.基于此，本文提出一个更加公平的算法，即将神经网络维数的初始值设置为~N＝M／2（一般地，假设M为偶数），这样兼顾了不同信源数条件下算法的收敛速度，并给出了基于稳定性判决器的神经网络维数的调整方案.

1 基于神经网络的BSS原理

考虑无噪的线性瞬时混合模型：N个相互统计独立的未知源信号s（t）＝［s1（t），…，sN（t）］T经未知混合矩阵A＝［ai，j］∈RM×N的传输后，由M个接收天线观测到混合信号x（t）＝［x1（t），…，xM（t）］T.BSS的任务是将观测信号通过解混矩阵W＝［wi，j］∈RN×M后，使得输出y（t）＝［y1（t），…，yN（t）］T是源信号s（t）的一个拷贝或估计.用矩阵形式表示为

基于神经网络的学习算法能够实时分离混合信号，解混矩阵W（t）可视为神经网络的权值矩阵（即wi，j为各网络节点在t时刻的权重），通过网络的无监督自适应学习，使网络输出尽可能相互独立.最早地，Herault和Jutten基于线性反馈网络，取得了先驱性的工作成果［9－10］.之后，文献［11］基于前馈网络，提出了一种更为稳健的Cichocki－Unbehauen算法，即

式（3）～（4）中：μ＞0为学习步长（通常是一个比较小的数值）；激励函数f（·）和g（·）为不同的非线性奇函数（典型的有f（y）＝y2sign（y），g（y）＝tanh（10y））；Λ＝［λi，j］为对角阵（一般取Λ＝I）.

2 信源数未知的BSS

2.1 稳定性判决器

定义神经网络的权值矩阵（即解混矩阵）的梯度方差V为

那么，平均梯度方差U的计算式为

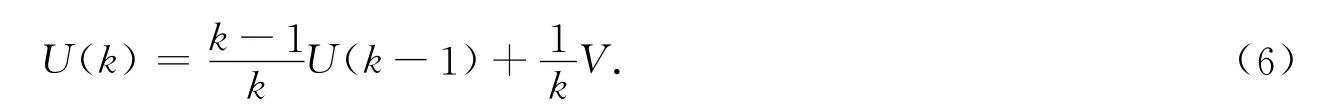
式（6）中：k＝1，2，…是U的时间索引.

根据信源数的估计值~N与真实值N之间的大小关系，描绘了3种不同状态下值的变化曲线，如图1所示.从图1中可以看出：当~N≤N时，U值在经历一段时间的增长之后，将稳定并保持在某一门限值之下；当~N＞N时，U值将一直保持单调增长趋势、趋于无穷.依此，可以构造一个稳定性判决器.即观测U值能否稳定收敛，若不能收敛，则说明当前的估计值大于真实值；若能收敛，则说明当前的估计值小于或等于真实值.

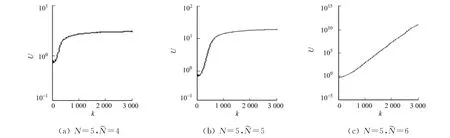
图1 3种状态下U的变化曲线Fig.1 Curves of Uin three states

2.2 基于公平神经网络的学习算法

由于信源数未知，因此在分离算法的初始化阶段应为神经网络维数设置一个初始值.不同的初始值决定了不同的网络维数调整方案，也影响了算法的收敛速度（即训练时间长短）.从数学统计意义的角度考虑，令＝M／2，这比单纯令＝M和＝2要更为公平.

文中提出的算法框架，如图2所示.首先，定义一个门限经验值ζ，以及一个观测时间经验值Tg.一旦初始值选定，将观测Tg时间长度内平均梯度方差U随时间的变化情况.若U（Tg）＞ζ（即U值无法收敛），可认为＞N，因此需要逐步降低神经网络维数，然后令＝－1，再进行新一轮Tg时间长度内的观测过程，直至U值趋于稳定；反之，若U（Tg）≤ζ（即U值收敛），可认为≤N.为了进一步判断究竟是＜N还是＝N，需要增加神经网络维数，令＝＋1，再进行新一轮Tg时间长度内的观测过程，直至U值发散.在观测阶段，为了保证收敛速度，赋予学习步长一个较大值，即k≤Tg时，μ＝0.05；观测阶段之后，为了保证收敛精度，赋予学习步长一个较小值，即k＞Tg时，μ＝0.005.

图2 本文所提出的算法框架图Fig.2 Framework of the proposed algorithm

3 仿真结果和分析

为检验该算法分离未知数目独立源的性能，采用下面6个平稳的、零均值的、独立的亚高斯信号作为源信号［5］，即

当采样频率为1kHz，采样点数为6 000，其时域波形如图3所示.混合矩阵A列满秩，矩阵元素是分布在［0，1］上的随机数.其他仿真参数为：接收天线数M＝8；信源数的初始估计值为4；门限值ζ＝30；观测时间Tg＝300个采样点.

将串音误差PI作为算法分离性能的衡量指标，即

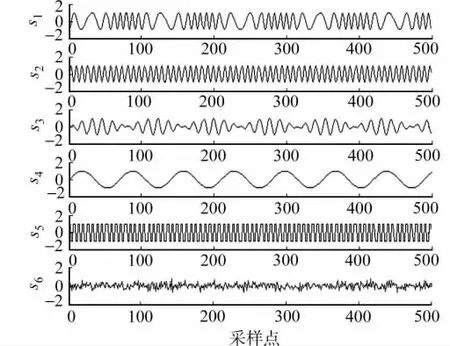
图3 6个源信号的时域波形图Fig.3 Waveforms of six source signals

式（8）中：｛cpq｝＝WA，PI越小说明分离效果越好.

仿真包含2部分：一个是较大信源数N＝6，取式（7）中的全部6个信号；另一个是较小信源数N＝2，取式（7）中的前2个信号.

在上述两种信源数条件下，一次典型仿真过程中算法对信源数的估计曲线，如图4所示.由图4可知：经历一段短的训练时间后信源数均能被准确地估计出来.

本文算法分离出的信号的时域波形图（为了显示清晰，仅给出了最后500个采样点），如图5所示.由图5可知：输出信号与源信号相比，虽然顺序和幅度上存在不确定性，但是时域波形是一致的，因此分离是成功的.

本文算法与文献［5］算法的PI曲线（取100次独立仿真结果的平均），如图6所示.两种算法都是基于稳定性判决器来逐步修正信源数估计值的.因此，对于令＝M的文献［5］算法来说，其收敛所需的训练时间与（M－N）成正比例关系；相应地，本文算法的训练时间与绝对值｜M／2－N｜成正比例关系.不难看出，本文算法更为公平，且对于比较小的信源数N，它在缩短训练时间方面的优势更加突出.图6结果也印证了上述分析：当N＝6时，两种算法几乎同时到达收敛状态；当N＝2时，本文算法的收敛速度显著快于文献［5］中算法，在收敛时PI值接近于0.

图4 本文算法对信源数的估计曲线Fig.4 Curves of estimated source number by the proposed algorithm

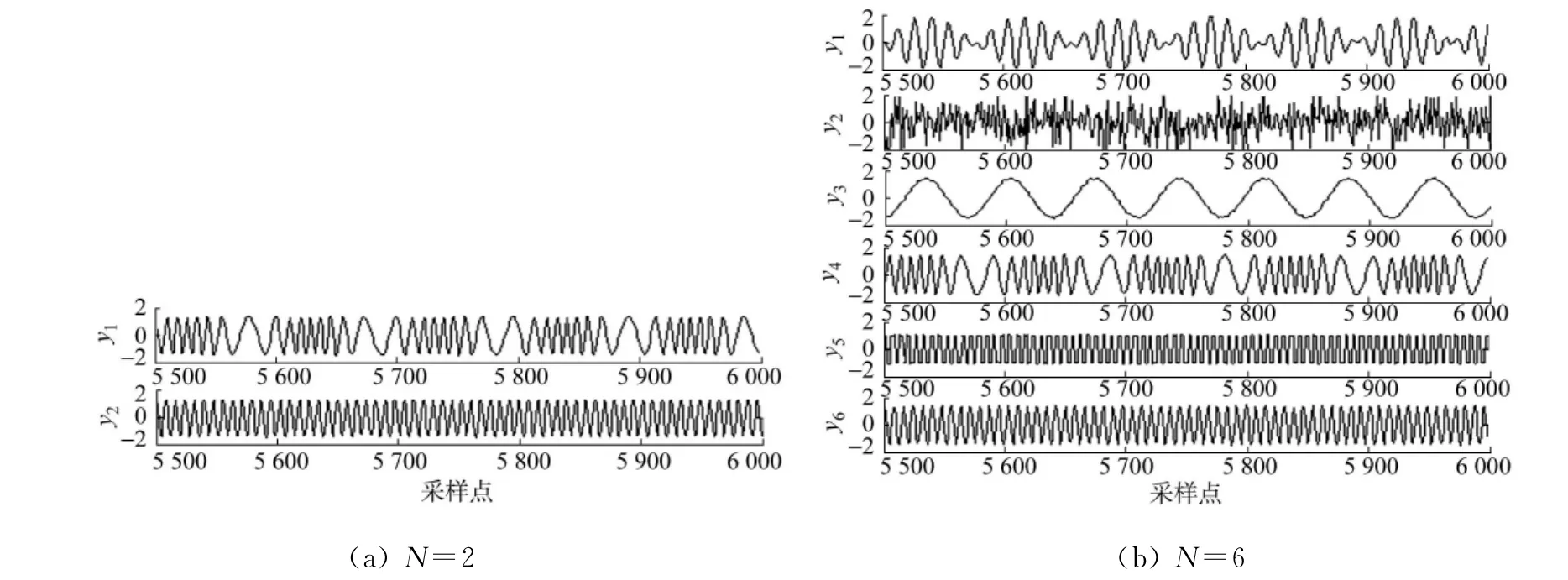
图5 本文算法分离出的信号的时域波形图Fig.5 Time domain waveforms of separated signals by the proposed algorithm

图6 两种算法的PI性能曲线Fig.6 PI curves of the two algorithms

4 结束语

针对更符合实际的信源数未知的情况，探讨了基于神经网络的超定盲信号分离.在Cichocki，Sun等研究的基础上，通过赋予信源数合理的初始估计值、构造稳定性判决器，提出了一种基于公平神经网络的分离算法.该算法通过逐步修正信源数估计值，能够准确估计出信源数真实值；兼顾了不同信源数条件下算法的收敛速度，在数学统计意义上显著缩减了训练时间，且无需预白化和数据降维，分离效果理想.因此，该算法优势突出，具有实用价值.

参考文献：

［1］ ROUTTENBERG T，TABRIKIAN J.Blind MIMO－AR system identification and source separation with finite－alphabet［J］.IEEE Transactions on Signal Processing，2010，58（3）：990－1000.

［2］ 杨彦龙，程伟，常洪振.基于FSS－kernel BSS方法的机械故障诊断［J］.北京航空航天大学学报，2012，38（11）：1557－1561.

［3］ CICHOCKI A，KARHUNEN J，KASPRZAK W，et al.Neural networks for blind separation with unknown number of sources［J］.Neurocomputing，1999，24（1）：55－93.

［4］ YE Ji－min，ZHU Xiao－long，ZHANG Xian－da.Adaptive blind separation with an unknown number of sources［J］.Neural Computation，2004，16（8）：1641－1660.

［5］ LIU Chan－cheng，SUN T Y，LIN Chun－ling，et al.A self－organized neural network for blind separation process with unobservable sources［C］∥Intelligent Signal Processing and Communication Systems.Hong Kong：IEEE，2005：177－180.

［6］ SUN T Y，LIU Chan－cheng，HSIEH S T，et al.Blind separation with unknown number of sources based on autotrimmed neural network［J］.Neurocomputing，2008，71（10）：2271－2280.

［7］ SUN T Y，LIU Chan－cheng，TSAI S J，et al.Blind source separation with dynamic source number using adaptive neural algorithm［J］.Expert Systems with Applications，2009，36（5）：8855－8861.

［8］ LI Hui，SHEN Yue－hong，XU Kun.Neural network with momentum for dynamic source separation and its convergence analysis［J］.Journal of Networks，2011，6（5）：791－798.

［9］ HERAULT J，JUTTEN C.Space or time adaptive signal processing by neural network models［C］∥AIP Conference Proceedings on Neural Network for Computing.New York：American Institute of Physics Inc，1986，151：206.

［10］ JUTTEN C，HERAULT J.Blind separation of sources，part（Ⅰ）：An adaptive algorithm based on neuromimetic architecture［J］.Signal Processing，1991，24（1）：1－10.

［11］ CICHOCKI A，UNBEHAUEN R.Robust neural networks with on－line learning for blind identification and blind separation of sources［J］.IEEE Trans on Circuits and Systems（Ⅰ）：Foudamental Theory and Applications，1996，43（11）：894－906.

Blind Separation Algorithm with Unknown Source Number Based on a Fair Neural Network

LI Kai1，LI Hui2，WANG Qi－zhi1
（1.College of Mechanical Engineering and Automation，Huaqiao University，Xiamen 361021，China；2.Institute of Communication Engineering，PLA University of Science and Technology，Nanjing 210007，China）

This paper proposes a fair neural－network－based algorithm.It initiates the estimatied source number to be a proper value，and constructs a stability discriminator，which can adjust dimensions of the nerual network and estimate the actual source number.Hence the algortihm is capable of separating sources sucessfully.Theoretical analysis indicates that it reduces the training time in mathematical statistical sense，and simulation results proves that it can converge quickly under different source number cases.

over－determined blind separation；source number；adaptive neural network；stability discriminator

TN 911.23

A

（责任编辑：黄晓楠 英文审校：杨建红）

1000－5013（2014）01－0011－05

10.11830／ISSN.1000－5013.2014.01.0011

2013－04－11

王启志（1971－），男，副研究员，主要从事复杂过程控制和智能控制的研究.E－mail：wangqz＠hqu.edu.cn.

福建省自然科学基金资助项目（A0640004）；华侨大学科研启动费资助项目（13BS305）；华侨大学横向科研资助项目（43201142）