电机故障识别模型优化研究
聂冰,郭永香,李文
(大连交通大学 软件学院,辽宁 大连 116028)*
0 引言
在工业生产领域中,电机已经成为最重要的动力来源.随着运行时间的增加,电机发生潜在故障或异常的频率也在逐渐增多,对设备的安全运行造成了极大的威胁.因此,利用故障诊断理论与技术及时、有效的监测电机故障是保证电机安全运行的重要手段,电机故障诊断方法研究为安全生产提供了有力的保证[1].
通用的故障诊断过程包括以下四个步骤:信息获取、数据预处理、特征提取以及故障识别,其中故障识别是故障诊断的核心.电机精确模型建立困难,而人工神经网络不需要精确的数学模型就能够逼近任意非线性函数,因此在故障识别中已广泛应用[2-5].电机故障机理多样,且同类的故障特征也会因为运行条件的改变而改变,这就要求构建的神经网络规模足够庞大、能够有效逼近复杂的非线性特性,而构建的网络计算复杂度也随之增加.因此,构建一个网络结构简单、训练效率高、识别准确的神经网络对电机故障诊断具有重要意义.
本文利用BP网络进行电机故障识别.针对神经网络模型复杂、依靠经验选取隐节点缺乏理论指导的问题,对网络进行了隐层优化,通过样本对模型网络的训练与测试验证了优化的故障识别模型的有效性.
1 电机故障识别模型的优化算法
1.1 故障识别模型结构
BP网络是误差反向传播的多层前馈神经网络,是目前应用最广泛的神经网络之一[6].网络结构需要确定输入层、隐层和输出层的节点数.故障识别模型自身的输入输出特征决定了输入、输出层的节点数,网络的输出节点由需要识别的故障特征确定,输入节点由采集的电机振动信号、定子电流等系统特征信号确定,隐节点神经元的激励函数采用Sigmoid转移函数.故障识别模型如图1所示.
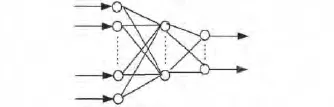
图1 电机故障识别模型
隐层的设计取决于隐层层数和节点数两个方面,是决定网络性能的关键.对于隐层层数,文献[7]指出三层神经网络在理论上能够逼近任意非线性函数;对于隐层节点数,选择过多,容易出现“过拟合”现象;选择过少,容易出现网络逼近能力不足.因此,隐层节点数的选择是网络结构确定的重点.本文根据系统模型的实际情况,利用隐层节点输出的相关系数自动调整节点数量,确定隐层节点的最优值,解决了常规方法中隐层节点数根据经验确定,缺乏科学性的问题[6].
1.2 利用相关系数优化神经网络
构造一个隐层节点数足够多的神经网络,通过计算各隐节点输出的方差和相关系数判断网络中是否存在冗余节点.隐节点x的输出方差s2x由matlab函数var(On)确定,On表示n个输入样本隐层节点的输出矩阵;两个隐节点x、y输出的相关系数rxy由matlab函数corrcoef(On)确定.
(1)优化合并条件
在网络训练过程中,首先设置合并时刻误差.若对训练样本的输出误差平方和小于合成误差,则进入优化合并阶段.当两个隐节点的相关系数|rxy|≥0.8,且两个节点方差s2> 0.001 时,说明这两个节点具有极强线性相关性,可以将两个节点合并之后删除其中的一个节点.
(2)优化合并方法[8]
设隐节点x和y的输出序列分别为Ox、Oy.当两个节点输出高度相关时,Ox和Oy满足一元回归线性方程:Oy=aOx+b.利用最小二乘法确定参数a和b.
将一元回归线性方程带入输出层任一节点i的输入中,有:

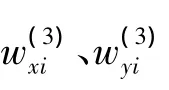
1.3 优化神经网络算法实现
结合经典BP神经网络学习算法,具体的隐节点优化神经网络算法实现如下[8]:
(1)网络初始化 ①输入层节点N、输出层节点M和隐层节点L;②输入层到隐层的权值矩阵wli=rand(.)l×i(1 ≤i≤N,1 ≤l≤L;)③ 隐层到输出层的权值矩阵wjl=rand(.)j×l(1≤j≤M);④合并误差ε1与终止误差ε2;⑤初始步长k=1;
(2)正向传播:输入n个训练样本,利用Sigmoid转移函数计算隐层、输出层的输出序列;
(3)反向传播:将误差信号从输出层经隐层再反传到输入层,调整各层权值使误差逐步减小;
(4)条件判断:当前训练误差error>ε1,转到步骤(2);若 ε1≥ error≥ ε2,转到步骤(5);error<ε2,则训练停止;
(5)优化参数计算:根据隐节点的输出矩阵计算隐节点的输出方差与相关系数;
(6)合并隐节点:若两个隐节点满足上述优化合并条件,则根据优化合并方法将两个隐节点合并后,转到步骤(2)继续训练.
2 应用举例
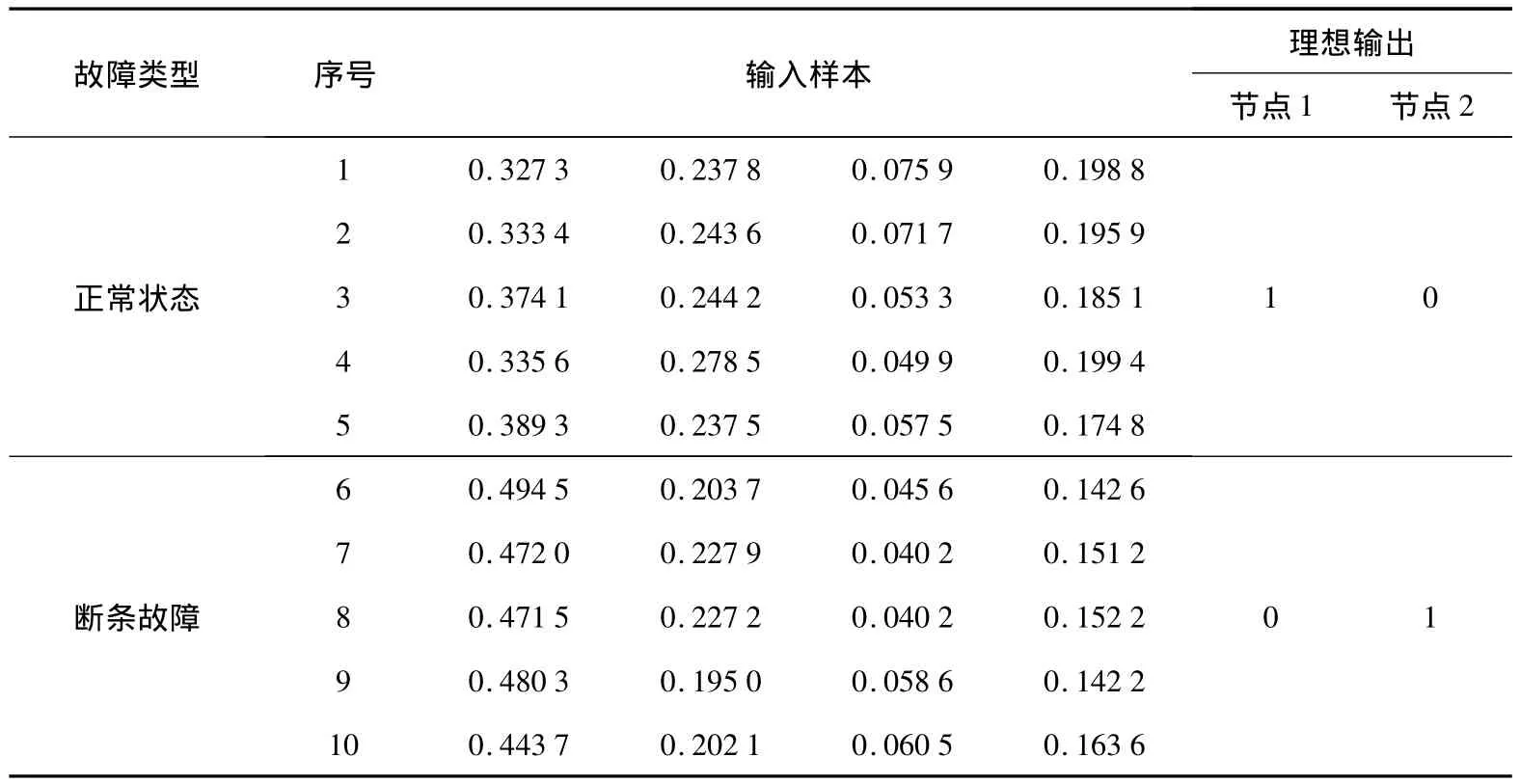
表1 模型的训练样本与理想输出
本文利用优化的电机故障识别模型检测电机性能良好与断条故障两种状态,故网络的输出节点为2个,分别对应两种状态.将采集的电机轴的径向振动加速度进行滤波与特征提取,使用其中4个子频段的能量比作为神经网络的输入,初始隐节点个数随机设定为8个,则采用的初始故障识别模型为4-8-2结构.使用10组特征提取后的振动加速度作为训练样本,12组数据作为测试样本,如表1、2所示,最大训练步长为3 000,合并误差 ε1=0.01,终止误差 ε2=0.001.由于初值权值随机选取,每次试验的结果不尽相同.图2是某次模型优化前后的训练曲线,与经典BP网络相比,优化后的网络收敛速度更快.这次学习优化过程中,在第470、471、572、712和713步隐节点进行了合并,合并的节点输出序列表现为高度正相关和负相关两种形式,部分输出序列如图3所示.优化之后的网络模型为4-3-2结构,经过结构优化训练停止时的误差为6.620 5×10-23,网络收敛符合预定目标.
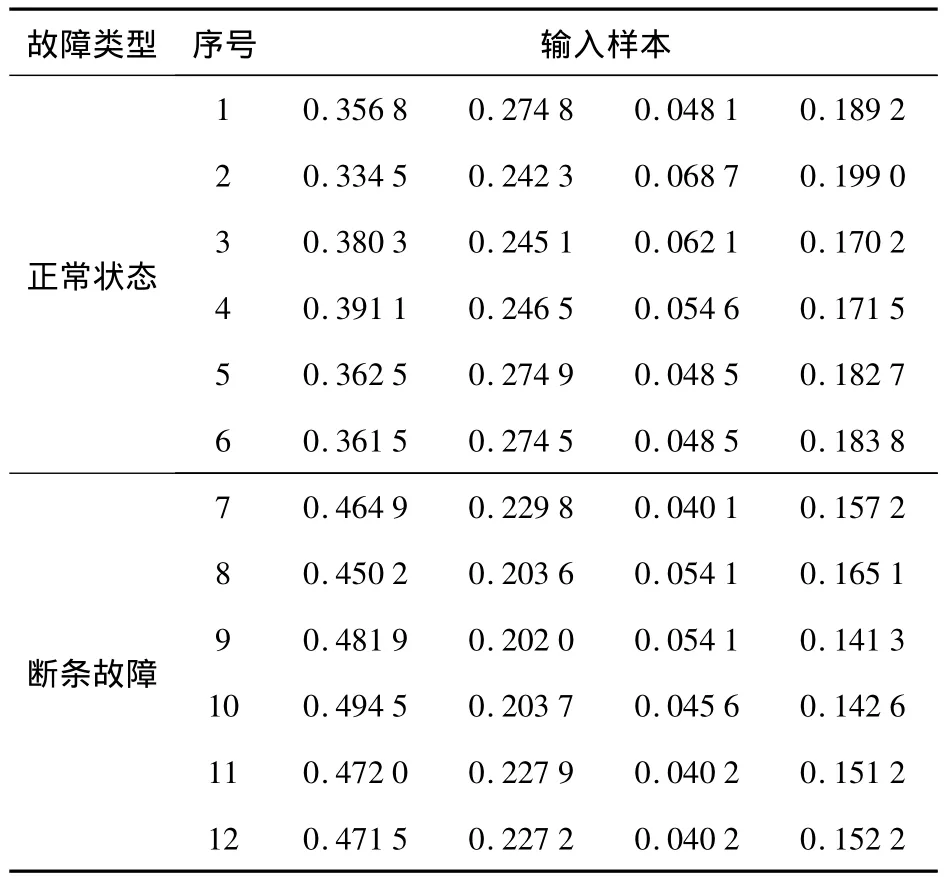
表2 模型的测试样本
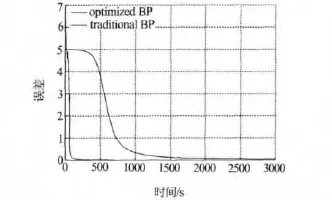
图2 模型优化前后的学习曲线
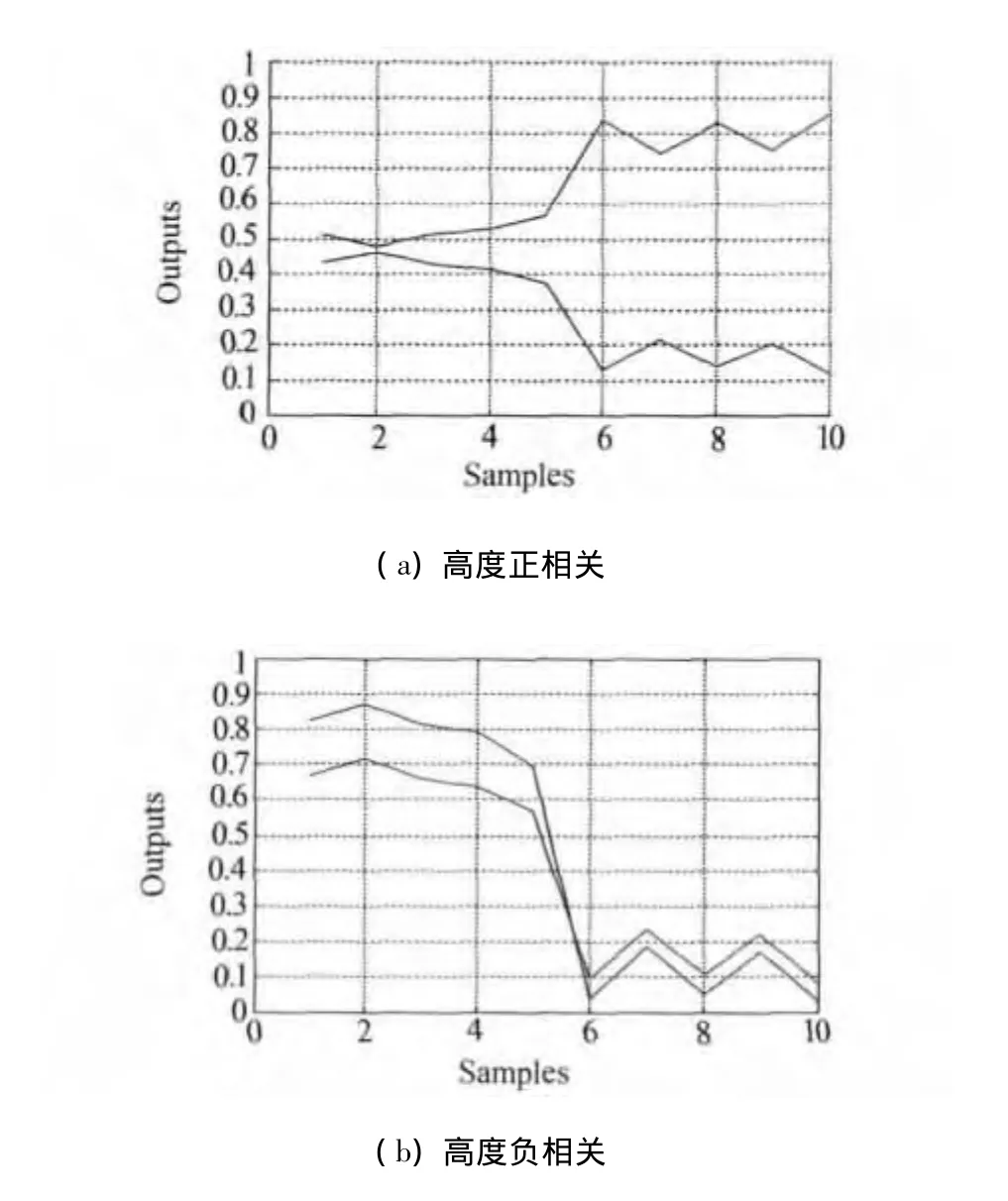
图3 隐节点输出序列图
利用表2中两种状态的12组测试样本对训练得到的优化模型进行测试.12组测试样本中的前6组对应的是电机良好状态,后6组对应电机断条状态.实际测试输出结果如图4所示,表明训练后的模型对故障诊断的效果良好,能够对电机故障准确分类.
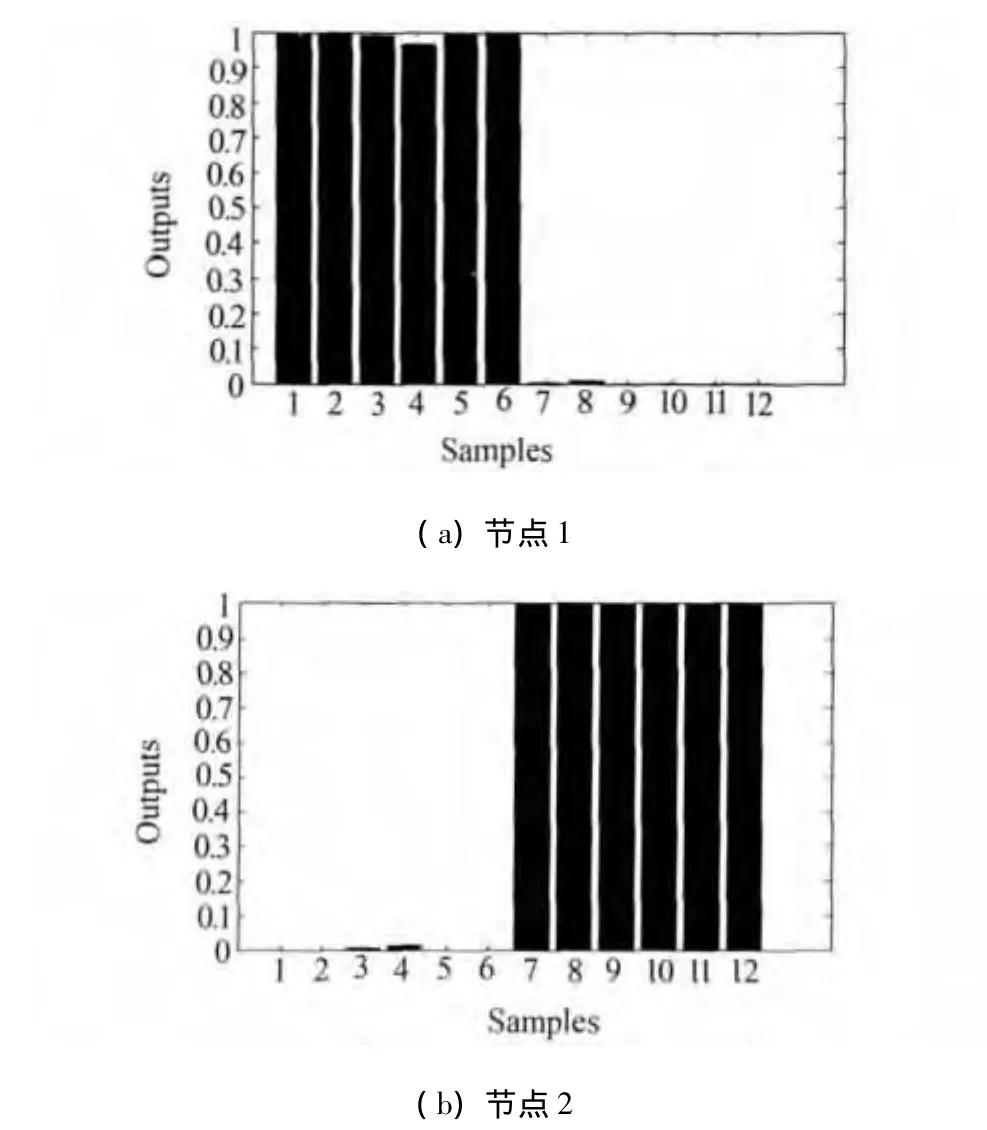
图4 测试样本在不同输出节点的输出
3 结论
本文提出了优化BP网络的电机故障识别模型的设计方法,在网络训练过程中利用相关系数优化了BP神经网络,使网络训练更加快速,逼近效果更好.该模型测试结果表明,所提出设计方法可行、所建立的故障识别模型有效.
[1]沈艳霞,纪志成,姜建国.电机故障诊断的人工智能方法综述[J].微特电机,2004(2):39-42.
[2]GHATE V N,DUDUL S V.Design of optimal MLP and RBF neural network classifier for fault diagnosis of three phase induction motor[J].International Journal of Advanced Mechatronic Systems,2010,2(3):204-216.
[3]MONICA ALEXANDRU.Analysis of induction motor fault diagnosis with fuzzy neural network[J].Applied Artificial Intelligence,2003,17(2):105-133.
[4]PARMATMA DUBEY,SUJATHA C.Motor Fault Classification using Wavelet Energy and Artificial Neural Network[J].International Journal of COMADEM,2009,12(3):24-31.
[5]SUBHASIS NANDI,HAMID A,TOLIYAT,et al.Condition Monitoring and Fault Diagnosis of Electrical Motors-A Review[J].IEEE Transaction on Energy Conversion,2005,20(4):719-728.
[6]唐万梅.BP神经网络结构优化问题的研究[J].系统工程理论与实践,2005,10:95-100.
[7]HECHT-NIELSEN,ROBERT.Theory of Backpropagation Neural Network[J].Neural Networks,1989(1):593-605.
[8]魏海坤.神经网络结构设计的理论与方法[M].北京:国防工业出版社,2005:125-141.

