谐波传动中不同材料柔性齿轮的有限元分析

张 驰，张 琳

(1.沈阳航空航天大学 民用航空学院，沈阳 110136;2.中国航天科技集团公司 九院16 所，西安710100)

0 引言

谐波齿轮传动具有体积小、重量轻、传动比范围广、传动精度高、移动准确、响应迅速等优越性能，广泛应用于航空航天、机器人、汽车、医疗器械等领域，谐波传动的设计研究也成为国内外学者研究的热点［1-4］。谐波齿轮的主要构件之一柔轮是一个薄壁壳体，在工作中承受交变应力的作用，容易发生疲劳破坏，对谐波齿轮的传动精度和使用寿命都有很大的影响，如何提高柔轮的性能直接影响着谐波齿轮的质量，该问题引起很多学者的兴趣。高海波等［5］研究了柔轮的结构参数对应力的敏感度影响，建立了杯型谐波柔轮的参数化等效接触模型;邓聪［6］建立了柔轮疲劳强度计算的数学模型，获得了柔轮各结构参数对疲劳强度系数的灵敏度;邓娟等［7］通过对杯型柔轮的应力分析，得到了柔轮厚径比和筒体长度对柔轮应力的影响规律;董惠敏等［8］用有限元方法求解了柔轮的应力场，并运用正交试验法分析了柔轮杯体结构参数对最大应力的影响。但是以上研究都是通过修改结构参数来提高柔轮性能，柔轮制备材料选择同样至关重要。

复合材料是两种或两种以上的单一材料复合而成的一种材料，使其具有单一材料所不能发挥的各种特性。以环氧树脂为基体，通过填加增强材料制成的复合材料有很多优良的性能［9］，在此领域的应用研究受到学者关注，并且进行了相关理论及实验方面的分析［10-12］。

为了研究不同结构材料对柔轮动态特性的影响，选择了三种不同的材料，即传统的钢质材料、碳纤维增强环氧树脂基复合材料(CF/EP)及玻璃纤维增强环氧树脂基复合材料(GF/EP)，并针对杯型和法兰型柔轮进行了模态分析，比较了不同材料柔轮的振动特性，为制备柔轮结构的选材提供依据。

1 柔性齿轮的有限元模型

以某杯型和法兰型柔轮为研究对象，首先利用三维建模软件Pro/E 建立两种柔轮的几何模型，在建模过程中根据实际情况进行合理的简化，然后导入有限元分析软件ANSYS 中，再对几何体划分网格生成有限元模型。

杯型柔轮和法兰型柔轮的基本几何尺寸如图1 所示，所有尺寸的单位均为mm。

图1 柔轮的基本几何尺寸

建立柔轮的有限元模型进行了如下假设:

(1)柔轮是静态加载薄壁轴对称结构，壳体变形符合小变形;

(2)波发生器是理想刚性的，外力作用在柔轮壳体上不会引起柔轮壳体的形状在径向发生改变;

(3)为了更好的确定柔轮的受载分布，用刚体-柔体接触单元处理柔轮和波发生器之间的力学关系;

(4)由于研究重点不是啮合问题，所以建模过程中忽略柔轮上的齿圈，通过增厚齿圈部位的厚度进而加大局部刚度来模拟齿圈。

(5)柔轮与箱体之间采用螺栓连接，因此将连接部位单元节点自由度完全约束。

单元类型的选择在某种程度上可以决定数据分析的精度，以及分析结果是否收敛，因此单元类型的选择至关重要。考虑柔轮变形程度较大的特点及计算过程中的时间消耗问题，采用实体单元solid95 和层单元shell91 来划分网格，这两种单元能很好的处理塑形、大变形等非线性行为。同时为了提高模型的精度，在应力集中部位均细化网格，最终生成的有限元模型如图2 所示。以合金钢材料为例，其中杯型柔轮共计30782 个节点，21546 个单元;法兰型柔轮共计29566个节点，20087 个单元。

图2 柔轮的三维有限元模型

为了比较新型复合材料柔轮和传统的钢制柔轮性能，选取了比较有代表性的合金钢42CrMo4，碳纤维增强环氧树脂基复合材料(CF/EP)及玻璃纤维增强环氧树脂基复合材料(GF/EP)，材料属性如表1 所示。

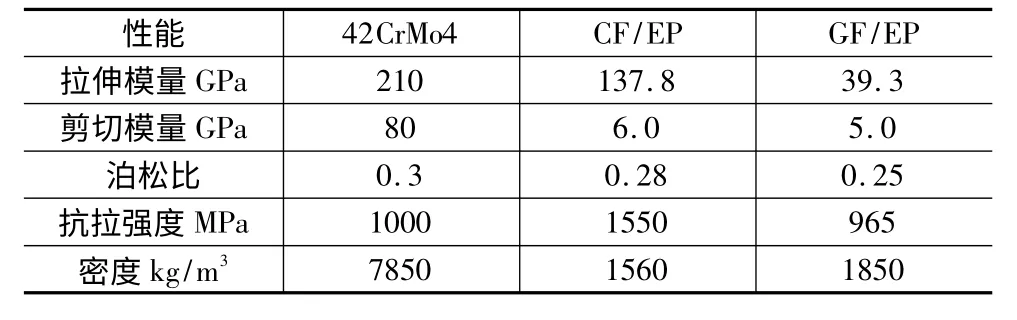
表1 三种材料的基本物理属性

2 模态分析

谐波传动中柔轮属于薄壁圆柱壳体，常处于变载荷工况下，目前对柔轮的外力计算没有明确的理论支撑，各国对其模态分析的标准亦不同。这里假设齿轮比为100，采用传递矩阵法对柔轮进行振动分析，定义如前所述的三种材料属性，分别求出其前五阶固有频率及振型，通过比较来分析材料属性对柔轮性能的影响。

三种不同材料的柔轮前五阶模态振型基本一致，如图3 所示。

图3 杯型和法兰型柔轮的前五阶振型

三种不同材料柔轮所得的振动频率对比如图4 及图5 所示。

图4 不同材料杯型柔轮的振动频率对比

图5 不同材料法兰型柔轮的振动频率对比

从图3 可知，两种柔轮的前五阶模态比较理想，与理论相符。同时通过图4 及图5 可知:

(1)杯型柔轮的振动频率略高于法兰型柔轮的振动频率;

(2)所选两种复合材料柔轮的振动频率均高于钢制柔轮的振动频率，玻璃纤维增强环氧树脂基复合材料柔轮的振动频率比钢制柔轮提高20%左右，碳纤维增强环氧树脂基复合材料柔轮的振动频率比钢制柔轮提高35%左右。

3 结束语

对两种不同形状的柔轮材料进行定义，通过模态分析得出:采用新型结构材料制备谐波传动柔轮可以提高其机械性能，环氧树脂基复合材料制备柔轮不仅可以减轻重量，还可以在某种程度上提高固有频率，降低共振发生的可能。

但是采用复合材料在制备工艺上存在一定的困难，因此可以考虑将钢制材料与复合材料相结合制备柔性齿轮，相关研究还需进行进一步的数值分析及实验测试。

［1］辛洪兵. 双圆弧谐波齿轮传动基本齿廓设计［J］.中国机械工程，2011，22(6):656 -662.

［2］Ostapski，Mukha. Stress state analysis of harmonic drive elements by FEM［J］. Bulletin of the Polish Academy of Science，2007，55(1):115 -123.

［3］张佼龙，周军，周凤岐.谐波齿轮综合误差对结构设计的影响［J］.机械设计与研究，2011，27(6):40 -43.

［4］李霞，张三川，陈维山.谐波摩擦传动柔轮结构参数对其应力影响分析［J］. 组合机床与自动化加工技术，2011，(2):24 -28.

［5］高海波，李志刚，邓宗全.基于ANSYS 的杯形柔轮结构参数对柔轮应力的敏感度分析［J］.机械工程学报，2010，46(5):1 -7.

［6］邓聪. 基于灵敏度分析方法的谐波减速器柔轮的疲劳强度研究［J］.机械传动，2012，36(10):31 -34.

［7］邓娟，杨荣松，郑香美，等. 基于ANSYS 的谐波减速器杯型柔轮应力分析与参数优化［J］.机械设计与制造，2012，(4):59 -61.

［8］董惠敏，李德举，齐书学.基于正交试验和有限元分析的谐波传动柔轮杯体结构优化［J］. 机械传动，2013，37(1):34 -38.

［9］苏航，郑水蓉，孙曼灵，等.纤维增强环氧树脂基复合材料的研究进展［J］.热固性树脂，2011，26(4):54 -57.

［10］Chen X X，Lin S Z，Xing J Z. Modeling of Flexspline and Contact Analyses of Harmonic Drive［J］. Key Engineering Materials，2010，419:597 -600.

［11］Kwiatkowski D，Nabiałek J，Gnatowski A. The examination of the structure of PP composites with the glass fibre［J］. Archives of Materials Science and Engineering，2007，28(7):405 -408.

［12］Dobrzański L A，Nowak A J，Bła˙zejewski W，et al. Nonstandard test methods for long-fibrous reinforced composite materials［J］. Archives of Materials Science and Engineering，2011，47(1):5 -10.