光栅投影双目立体视觉测量方法的研究*

刘 江，梁美芹，刘晓明

(北京科技大学机械工程学院，北京 100083)

0 引言

随着数字投影技术和计算机视觉理论的快速发展，光栅投影的双目立体视觉测量已成为三维视觉测量的一个重要方面，在逆向工程中具有广泛的应用前景，特别是在长度超长的大型构件测量中［1］。光栅投影双目测量系统是利用计算机编程生成一系列正弦光栅，通过数字投影仪依次投射到被测物体表面，摄像机拍摄到受物体表面调制的变形光栅图，通过格雷码和相移法解相位恢复出连续相位分布，利用相位值准确快速的找得左右相机中的匹配点，最终利用视差原理重构三维物体。

1 测量原理

双目光栅测量系统组成如图1 所示，硬件部分包括双摄像机，双12mm 定焦镜头，数字投影仪，计算机等。

光栅投影的双目立体视觉是基于三角形视差原理获取物体的三维信息，即两个摄像机的像平面和被测物体之间构成一个三角形。在两个摄像机已立体标定的情况下，两摄像机的位置关系是已知的，再利用相似三角形的关系便可得到两摄像机公共视场内的特征点的三维坐标。

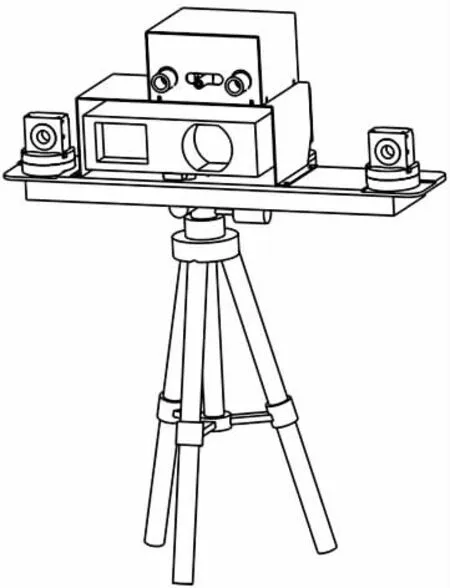
图1 系统结构装配图

2 相位求解

本文投射光栅到物体表面，增加被测物体表面的特征信息，以便于匹配。经过编码，两个相机拍摄到的同一场景的两幅图片中，满足码值相同和极线约束条件的对应点即为一对匹配点，然后利用双目立体视觉测量的三角视差原理计算出空间点的坐标。

2.1 相移法

相移法(Phase-shifting)［2］是利用多张有相同的相位增量作相位重建的一种测量算法。投射如图2 所示的计算机编程生成的四幅满足正弦强度分布且初始相位差为π/2 的光栅条纹在待测物体表面。

图2 相移法中正弦光栅图

正弦光栅通过投影仪投射到物体表面，CCD 摄像机拍摄经物体表面高低起伏调制变形的光栅条纹图，如图3 所示，变形的光强分布函数为:

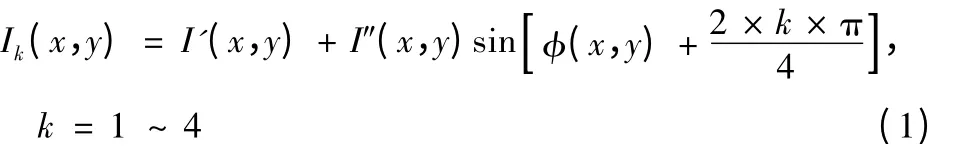
式中，Ik(x，y)为该像素的光强，φ(x，y)为初始相位，I'(x，y)为条纹背景光强，I″(x，y)为调制强度，k为该图像在相移图像中的序号。

每张图像的光强分布为:

对上式化简变形可得相位主值

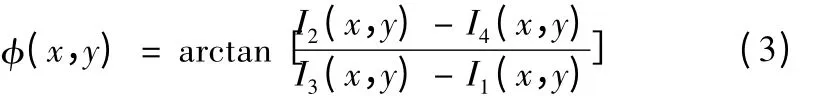
由于本研究中采用的是彩色CMOS 相机［3］，在拍摄过程中不可避免会有外界光线及噪声的影响，所以需先对图像进行滤波、二值化、灰度化预处理，然后用四步相移法，得到如下图4 所示的相位图，其中图4a为二维相位图，4b 是三维相位图。图5 提取其中某行数据绘制的二维图像，从图中可以看出，相位的取值范围是(-π/2，π/2)，我们必须加以修正。

图3 摄像机拍摄的变形光栅条纹图

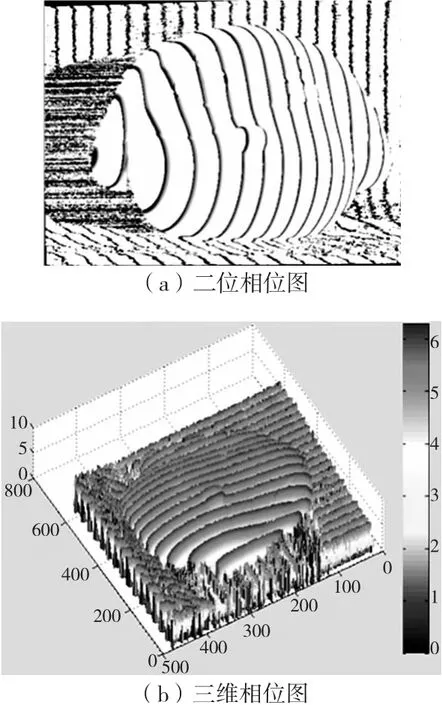
图4 相位图

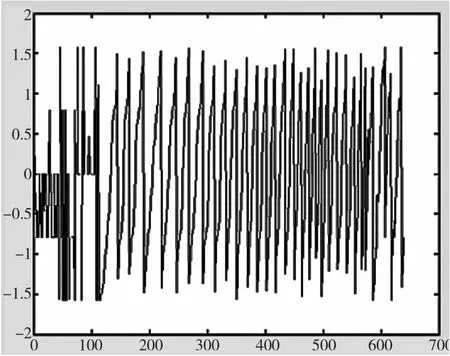
图5 某行相位值得数据图

2.2 相位主值的修正

由反正切函数的特性可知，解出的相位主值φ(x，y)的值域区间为(-π/2，π/2)，但实际的相位主值应位于(0，2π)，因此需要分析其分子及分母正负的具体组成结构，才能清楚地知道相位角到底位于哪一象限，进而才能求得真实的相位值。

如下图6 相位角示意图，图內的正负号表示相位角位于此象限时，其正切函数的正负值，可以从分子及分母(即(I2-I4)，(I3-I1))的正负号来判定相位角具体的位于哪一象限，将反正切后的相位值补偿成(0，2π)区间的相位值，如图7 所示。

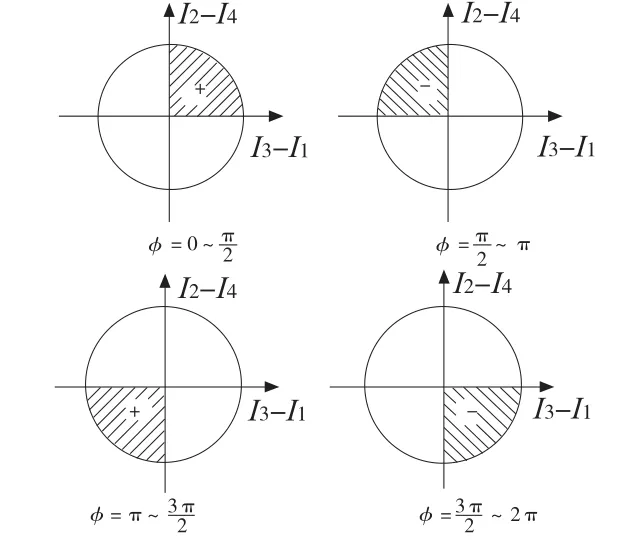
图6 相位角示意图

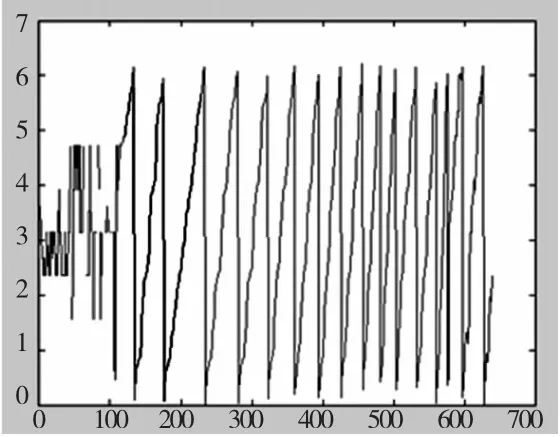
图7 相位主值修正后某行的相位值

可见，经过修正后，相位角的周期加倍，幅值增加，在0～2π 之间相位角越来越大，在2π 这个点就变成0，但是相应阶数就增加了1。

四步相移法得到的相邻像素间的相位差落在(0，2π)，但当遇到不连续的相位边界时，就会产生2π 的跨越落差。我们需在不连续处进行相位展开(消除2π突变)，便可获得连续的相位分布图［4-5］。如图8 所示是四步相移法后的不连续相位分布，图9 应是进行相位展开之后获得的连续相位分布。

图8 不连续相位图分布

图9 续相位图分布

2.3 相位展开—格雷码加相移法

考虑到三角函数的周期为2π，完整的相位值应为:

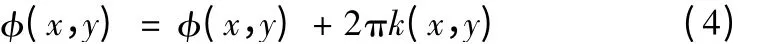
式中，φ(x，y)为相移法得到的相位主值，k(x，y)为各条纹的周期次数。

当格雷码［6］的周期与正弦光栅周期相等时，则相位主值相差一个周期对应的格雷码值相差1，根据这个规律，可以利用格雷码与正弦光栅相结合的方式来获取连续相位值［8］。格雷码编码通过图10 的流程图解码，结合上述获得的相位主值得到如图11 所示的连续相位值，图12 为上述对应数据的解相结果。φ(x，y)为相位主值，G(x，y)为该像素的格雷码值，ψ(x，y)为展开的相位绝对值。

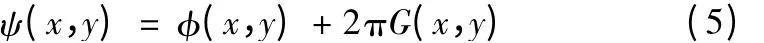
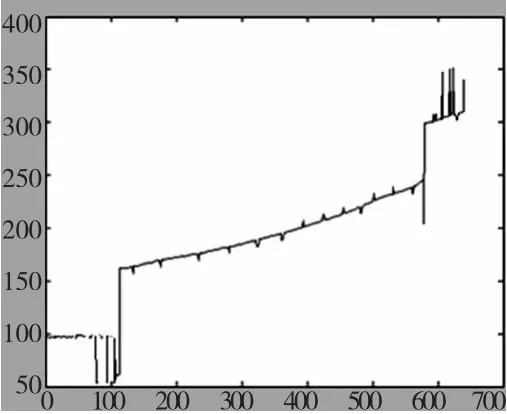
图12 开后某行的相位值

3 系统标定与立体校正

为了完成二维平面图像到三维立体场景的转变，需要精确的确定摄像机的内外参数，即摄像机标定［7，9-10］。

下图13 为世界坐标系、摄像机坐标系和图像坐标系之间的关系转换。

图13 像机坐标系与世界坐标系关系

假设空间中一点P在世界坐标系与摄像机坐标系下的齐次坐标分别是(XW，YW，ZW，1)T与(Xc，Yc，Zc，1)T，则存在如下关系:

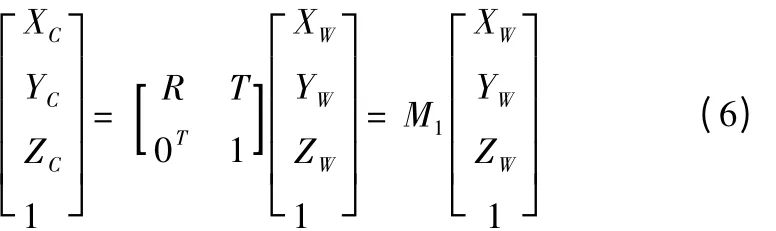
式中，R 为旋转矩阵;T 为三维平移向量;

点P 在图像上的成像原理近似采用针孔模型表示则有:

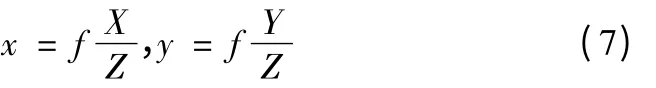
用齐次坐标与矩阵表示上述投影关系为:

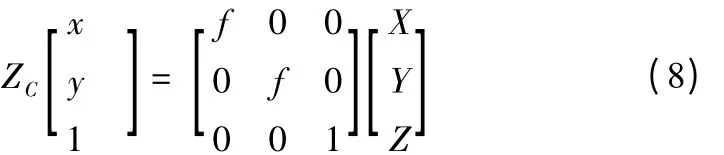
将式公式(6)和公式(7)带入上式得

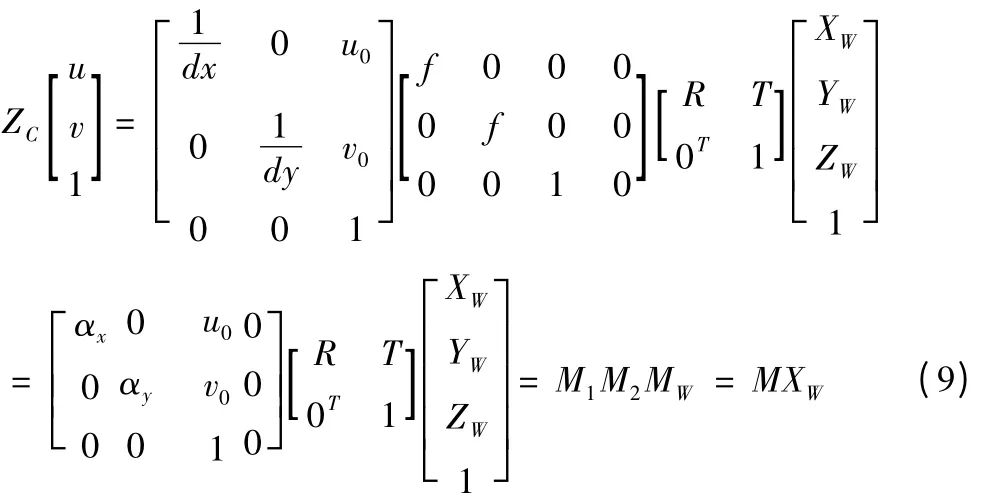
其中，αx = f/dx，αy = f/dy;f为相机的焦距，称为主距;Ou为主点。M为透视投影矩阵;M1为摄像机内参数矩阵，M2为摄像机外参数矩阵。摄像机的标定就是确定摄像机的内、外部参数。

张正友平面模板标定法中平面标定模板制作简单，运算速度快，标定结果准确，因此本研究采用张正友平面模板标定法进行系统标定［1］。

张正友平面模板标定法以标定板所在平面为世界坐标系的XW—YW平面，则标定板上所有特征点zw=0。用ri表示旋转矩阵R的第i列向量。对于平面模板上的点都有:

其中，单应性矩阵H表示平面模板上的点与像点之间的映射关系。通过提取标定板图像上的角点坐标，根据公式(10)便可计算出每个视场的单应性矩阵。因为H =[h1h2h3]，则有:

从而可得:

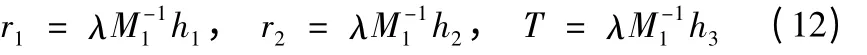
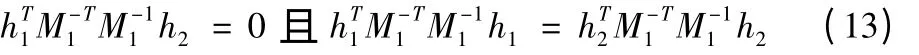
可见，摄像机的内、外部参数可以由棋盘坐标系之间的转换关系计算得到。

图像立体校正就是利用标定过程中得到的参数，对左右相机拍摄的两幅图像首先进行了透视变换，分别将极点移至无穷远处，极线束变为两两平行的一组直线;然后进行相似变换，让各极线均平行于图像坐标系的横轴，即极线水平;最后再进行错切变换减少畸变，使水平方向上的图像畸变最小。经过一系列变换把两个相机的立体几何结构变成标准的外极线几何结果，如图14 所示。

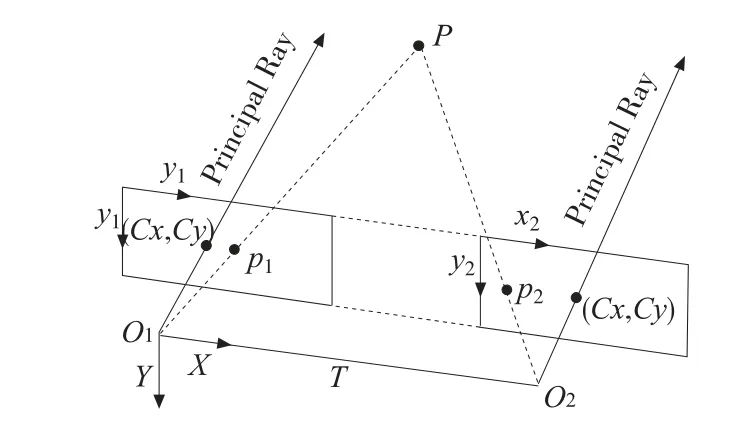
图14 体校正后的几何结构

经立体校正后，两摄像机的极线平行且等高即相当于平视双目立体成像，匹配对应点处于水平线上，大大降低了匹配搜索难度，提高了运算速率。

4 立体匹配与三维重建

4.1 立体匹配

双目立体视觉获得三维空间点云是通过计算目标点在左右两个视图上形成的视差得到，所以我们首先要把该点在左右视图上两个对应的像点匹配起来。我们通常所说的匹配即为寻找公共视场内的特征点的过程。在立体匹配的过程中需要满足以下几个约束:

(1)唯一性约束。一幅图像的每个像素只能对应于另一幅幅图像中的一个像素。

(2)连续性约束。物体的表面是连续的，则物体表面上的点在图像上的投影也是连续的，其视差也是连续的。

(3)顺序一致性约束。一幅图像的一条极线在另一幅图像中有一条对应极线，该对极线上的匹配基元的序应该是相同的。

(4)极线约束。在立体几何中，对于从不同角度获取的同一场景的两幅图像来说，对应点之间应满足极线约束，即一幅图像上的任一点，在另一幅图像上的对应点一定位于该点对应的极线上。

对图像进行了立体校正后，此时左右图像的极线平行且等高，所以匹配时只需在行方向上寻找，又因为格雷码周期与相位周期相同，把格雷码值乘以2π 加上相位主值得到了线性的相位绝对值，可见，满足匹配条件的对应点应位于同一高度而且具有相同的绝对相位值。

4.2 三维重建

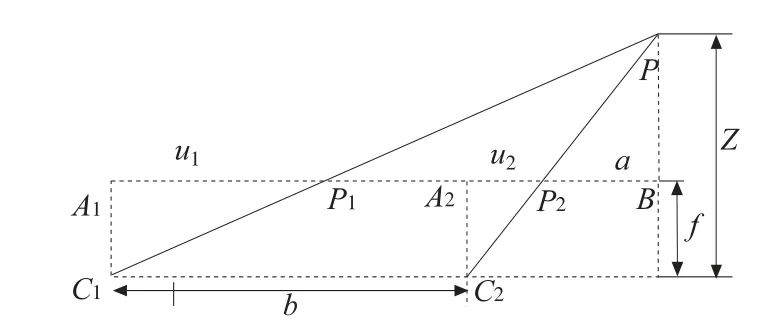
图15 目视差原理图

如图15，两摄像机的基线距为b，左图像的主点坐标为(cx，cy);空间点P 的世界坐标为(X，Y，Z) ，在两摄像机成像平面上的像点分别为(u1，v1)和(u2，v2)，其中视差d = u1- u2。根据成像的几何比例关系，对于左右摄像机关系如式(14):

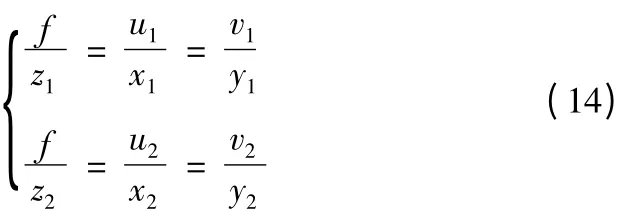
由于，两摄像机的成像平面位于同一平面内且在垂直方向对齐，因此，世界坐标系与摄像机坐标系的关系表述如下:

联立(14)和(15)两式可得:

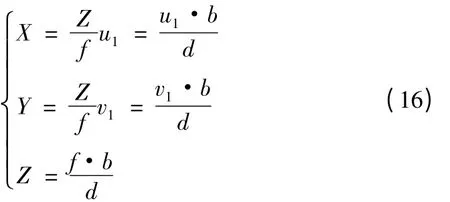
式(16)把三维物体的深度Z与视差d直接联系起来，而深度反映了三维空间信息。由于立体匹配已将左右图像的对应点匹配起来了，便可计算出特征点的视差，进而结合立体标定获得的系统参数，便可计算出特征点的三维坐标值。

5 实验

本研究选择白色玩具狗头作为实验对象，利用图

1 所示测量系统采集到如图16 所示的包含被测物体表面高度信息的光栅变形图。

图16 集到的变形光栅图

利用四步相移法解得初始相位主值，再进行相位主值的修正，进而结合格雷码进行相位展开获得连续的相位值，以此为据进行左右图像的立体匹配，获得视差图，再借助于系统的标定信息生成模型的三维点云效果图以更直观地检验三维测量信息得到的重构效果如图17 所示。

图17 三维点云图

实验结果表明，在被测物体本身颜色信息较为单一以及物体高度没有出现剧烈的跳变时，本研究能在投影多幅辅助光图像前提下有效地实现三维测量并达到较为理想的精度，而且算法流程易于实现。

从点云图17 中可以清楚的看到，点云密度不均，局部有明显的点云缺失现象，虽然这些问题可通过后续的处理得到改善，但还没有从原理上解决问题，这是本系统存在的一个弊端。本实验只采集了一组实验图片，未考虑环境中噪声的影响，从图17 中左边耳朵处，可以明显的看到噪声点的影响。此外图中玩具狗头耳朵处位于同一周期的点云出现了局部缺失现象。针对以上问题，可以在通过以下方法来改善:

(1)系统标定中角点提取是在手动选取角点的四周轮廓的基础上进行的，精度不如自动提取的高，会产生一定误差。

(2)光栅图是数模转换后得到的，不是标准的正弦，必须通过实验来调节相机、投影仪的参数。

(3)减少噪声影响，可采取多次采集求平均值、后处理等方法降低环境的影响，提高系统的精度。

6 结束语

针对光栅投影三维测量技术的原理进行了阐述并且给出了结果。实践证明光栅投影法具有检测过程完全非接触、数据空间分辨率高、一次性瞬间投影直接实现三维物体形状检测的特点，便于实际应用，具有较高研究价值和发展前景。此外，光栅投影的双目立体视觉测量方式，由于测量平台可以随意放置到大尺寸或超大尺寸构件周围的任一位置，不需要运动平台，可实现自动拼接，测量速度快，操作简单方便，因此在大尺寸或超大尺寸构件的表面测量上具有广阔的应用前景。

［1］马颂德，张正友. 计算机视觉- 计算理论与算法基础［M］.北京:科学出版社，1998.

［2］刘晓辉. 基于格雷码与相移结合的双目立体视觉测量研究［D］. 福建:华侨大学，2011.

［3］刘荣生.CCD 与CMOS 传感器的发展与应用［J］.影像材料，2003(5):7 -11.

［4］张培恩. 以DLP 发展光学立体视觉微测量系统之研究［D］.台湾:国立台湾大学，2006.

［5］刘菲. 基于相位测量法的光学三维形貌测量研究［D］.山东:山东师范大学，2008.

［6］王震. 基于光栅投影的三维模型测量系统关键技术研究与实现［D］. 南京:南京航空航天大学，2007.

［7］Zhang Zhengyou.Flexible camera calibration by view a plane from.Calibrate Research，1998.

［8］尹丽萍，于晓洋，吴海滨.格雷码与相移结合的结构光三维测量技术研究［J］. 哈尔滨理工大学学报，2007，12(5):5 -8.

［9］Tsai R Y. An efficient and accurate camera calibration technique for 3D machine vision［J］. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition，1986:364 -274.

［10］Sansoni G ，Carocci M ，Rodella R. 3D vision based on the combination of gray code and phase shift light projection［J］. Applied Optics，1999，38(31):6565 -6573.