永磁直线伺服电机端部法向力波动分相补偿控制*

夏加宽，沈 丽，彭 兵，孙宜标

(沈阳工业大学 电气工程学院，沈阳 110870)

0 引言

单边平板式永磁直线伺服电机(PMLSM)具有推力密度大、加速度高以及实现进给系统“零传动”等优点［1］，正在成为高精度高速度数控机床的主要功能部件，广泛应用于微机械制造、微型零件操作与装配、超精密加工、半导体制造设备以及光电等领域中［2］。

单边平板式PMLSM 电枢铁心的开断破坏了磁路和磁通分布的对称性，产生了直线电机所特有的端部效应［3］，端部效应一方面会引起电机的推力波动，另一方面还会引起法向力的波动。法向力波动一方面以摩擦力扰动的形式体现出来引起推力波动;另一方面还会引起机床的震动。对于直线电机推力波动产生机理和削弱方法的研究，已取得了丰硕的成果［4-5］。而对平板式PMLSM 法向力波动的研究还处于初级阶段，其抑制方法主要是在电机本体设计上采取措施［6-8］。这些优化方法能够在一定程度上减小PMLSM 法向力波动，但针对端部效应引起的法向力波动的优化效果不明显，同时还可能引起电机动子的俯仰运动。尤其是对于成品电机，无法在电机本体上再采取措施。因此必须从控制角度进一步抑制端部效应引起的法向力波动对伺服控制精度的影响，行之有效的办法是进行补偿控制。文献［9-10］采用迭代学习控制和离散重复控制来抑制PMLSM 端部效应所引起的周期性力的波动，仿真结果证明方法的有效性，但运算量较大，实时性不强。文献［11］采用有限元法预测PMLSM 磁阻力模型通过在磁场定向控制方式中注入瞬时电流来进行补偿;但模型中没有体现端部效应引起的法向力波动的特殊分布规律。

本文首先分析研究法向力波动的产生机理及波动的特殊分布规律，通过有限元计算数值分析获得端部法向力波动的分析模型，利用此模型实现直接准确的扰动补偿。提出基于推力不变法向力波动最优的A、C相绕组分相补偿控制策略来抑制端部效应引起的法向力波动，进一步提高系统的伺服精度。本文通过仿真以及实验验证了该补偿方法的有效性。其理论成果为抑制法向力波动提供理论指导，为开发精密直线伺服系统提供有效的理论依据和可靠的实现手段。

1 PMLSM 端部法向力补偿模型

1.1 单端端部法向力模型

单边平板型PMLSM 的物理模型如图1 所示，在运行过程中动、定子之间存在较大的法向力波动，即使在电机绕组不通电流的情况下，也存在着明显的端部法向力，对高精密机床而言，它是引起法向力波动的主要原因。

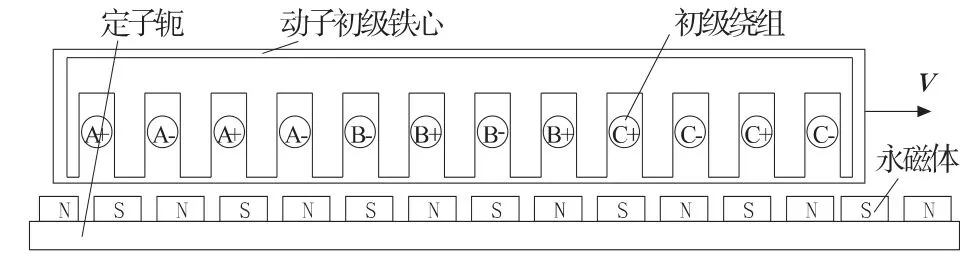
图1 11 极12 槽PMLSM 物理模型

由于端部磁场畸变，端部磁场分布相当复杂，很难用数学方法描述，因此本文采用有限元方法对两台单端无限长无槽PMLSM 进行分析计算，图2a 为右端无限长无槽PMLSM 模型，图中电机动子以速度v向右移动，左端部受到的力为feN1，动定子之间的相对位置为x;图2b 为左端无限长无槽PMLSM 模型，图中电机动子以速度v向右移动，右端部受到的力为feN2，动定子之间的相对位置为x;针对图2 所示的模型进行有限元计算得出两单端端部法向力分布，如图3 所示。

图2 单端无限长无槽PMLSM 模型

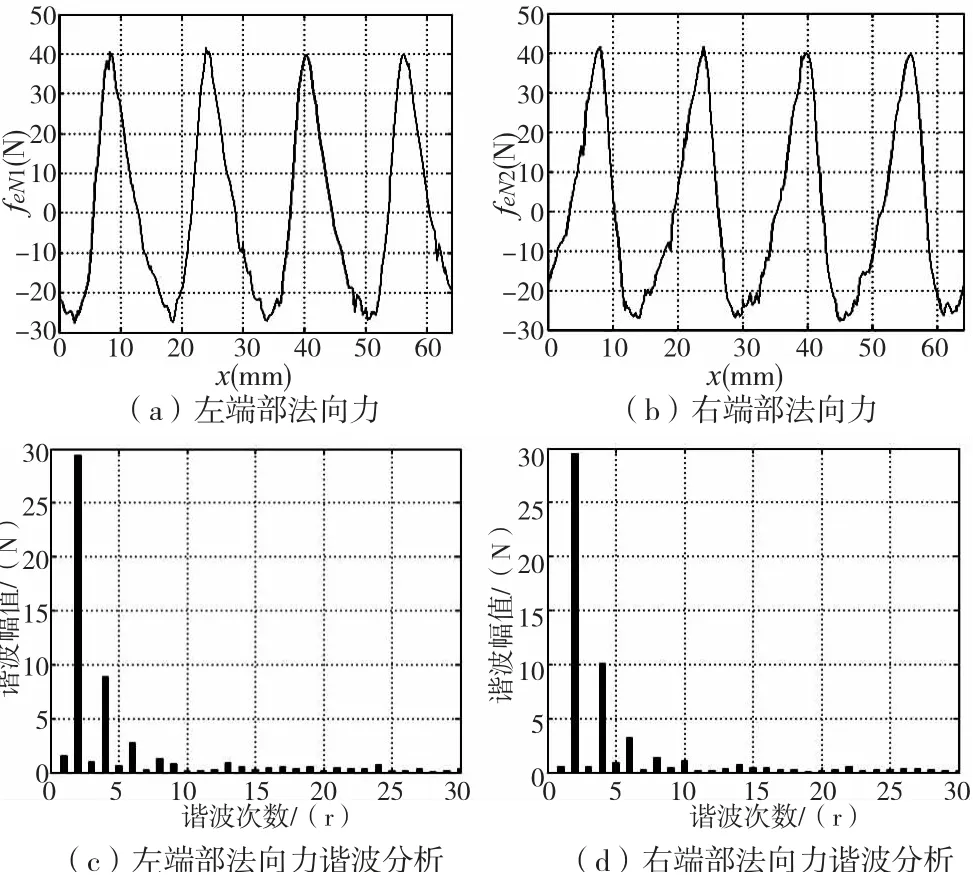
图3 单端端部法向力及谐波分析

对图3 所示的两单端端部法向力进行数值分析，采用四阶傅里叶曲线拟合，得出其数学模型:

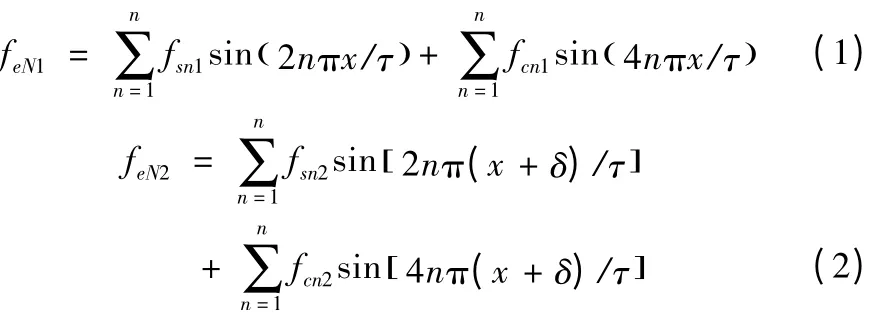
式中x为动子相对定子的位置函数;τ 为极距;fsn1、fsn2、fcn1、fcn2分别为两端端部法向力波动效应系数;δ=2pτ-l，其中l为动子长度，p为极对数。由图3c、d可知两单端端部法向力的谐波成分主要是二次谐波。

1.2 端部法向力补偿模型

PMLSM 运行时，动子同时受到端部推力feT1、feT2以及端部法向力feN1、feN2，如图4 所示。在分析端部效应对推力波动的影响时，对两单端端部力进行求和计算，求其合力feT = feT1+feT2，并采取优化动子长度的方法减小切向端部合力，从而减小端部效应对PMLSM推力波动的影响［12］。但在分析端部法向力对法向力波动的影响时，不能简单地集中在一点求其合力，而应该考虑机床用PMLSM 滚动轴承安装结构，将两单端端部法向力按照安装位置函数作用到A、B两个支撑点得到两个力fZ1、fZ2，这两个力作用在PMLSM 动子上，当同为正或同为负时，能够引起法向力波动;当一正一负时，它们并不能相互抵消，而将引起电机动子的俯仰运动。

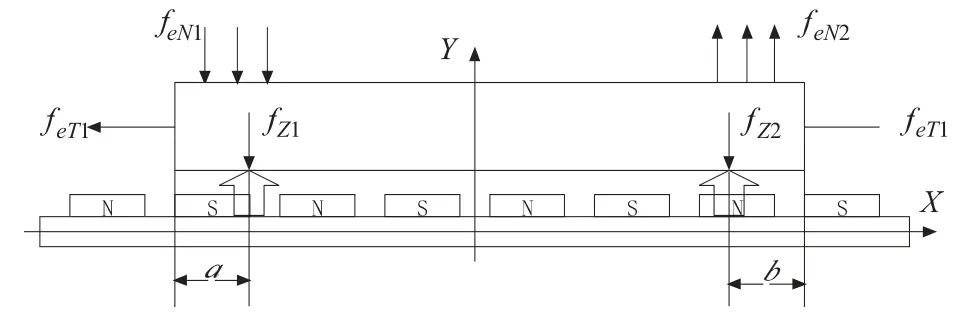
图4 无槽PMLSM 端部法向力分布模型

结合两单端端部法向力模型以及安装位置系数得出法向端部力的分析模型即力补偿模型:

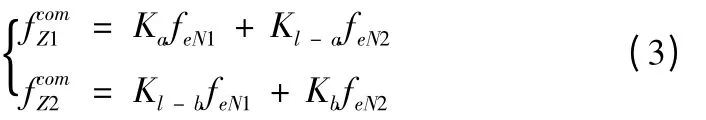
式中Ka、Kl-a、Kl-b、Kb分别为左右两端对应的安装位置系数。将式(1)、(2)中的二次谐波分量代入式(3)得:

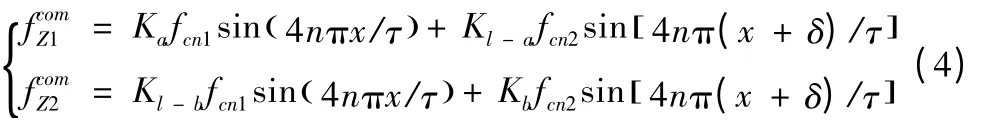
2 分相补偿控制

2.1 分相补偿控制原理

在近极槽PMLSM 中，多采用特殊相带绕组分布。以图1 所示的11 极12 槽为例，A相和C相绕组分布在电机的两端，B相绕组分布在中间，可以分别在A相、C相绕组中注入瞬时补偿电流来抵消端部法向力，从而减小端部效应对法向力波动的影响。

综合分析有限元计算结果和法向端部力的分析模型得出A相和C相绕组电流的补偿模型，依据补偿模型注入瞬时电流，抑制端部法向力波动，减小其对伺服系统精度的影响，这种控制策略称为分相补偿控制策略。

高性能永磁直线伺服电机通常采用转子磁场定向的矢量控制技术，采用id=0 控制方式，根据电机运动方程建立双闭环控制系统。

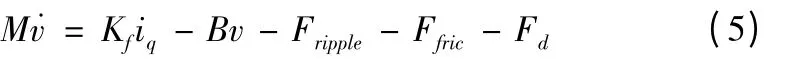
式中Fripple = Fcog + Fend，Fcog为齿槽推力波动，Fend为端部推力波动;Ffric = Fss +μrFn，Fss为摩擦力，μr为滚动摩擦系数，Fn为法向力;M为动子质量;Kf为推力系数;iq为交轴电流;B为粘滞摩擦系数;v为电机速度;Fd为负载阻力。

在矢量控制策略基础上，加入前馈电流补偿器，就构成了分相补偿控制策略的原理框图，如图5 所示。

图5 分相补偿控制策略原理框图

PMLSM 在运动过程中，利用端部法向力的补偿模型，根据直线电机当前的位置，可计算出动子运动过程中受到的端部法向力，经过运算后得出A/C相电流补偿模型。根据电流补偿模型设计前馈补偿器分别对A/C相电流进行补偿，从而抑制端部法向力在电机运动过程中造成的扰动，提高系统的控制性能和伺服精度。

2.2 A/C 相电流分相补偿模型

根据矢量控制基本思想，在三相交流电机磁场定向坐标上，将电流矢量分解成产生磁通的d轴电流分量id和产生推力的q轴电流分量iq，两者互相垂直，彼此独立。绕组通入电流，就会产生磁动势，等效的d轴和q轴磁动势分别为:

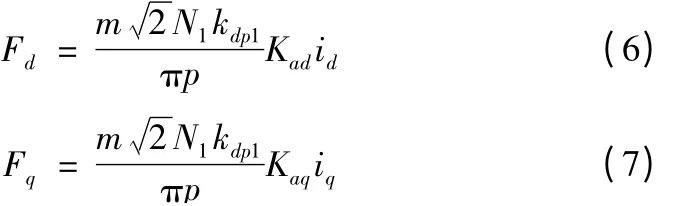
式中，m为相数，N1为一相绕组的串联匝数，kdp1为基波绕组系数，Kad和Kaq分别是d轴和q轴的反应系数。由电机学原理可知，磁动势是机电能量转换的关键，PMLSM 的法向力主要与d轴磁动势即电流分量id有关。

式中kmmf为磁动势效应系数。由矢量控制原理可知:

针对法向力波动进行补偿时，假设iq=0，将式(8)、(9)代入式(10)可得出A/C相分相补偿模型:

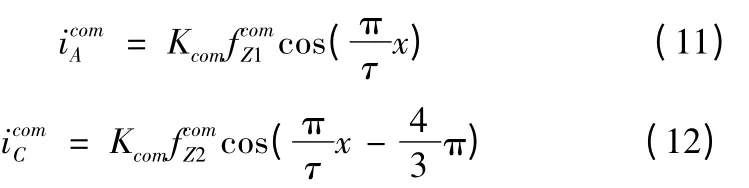
从而设计提取A/C相瞬时补偿电流的模块，如图6 所示。

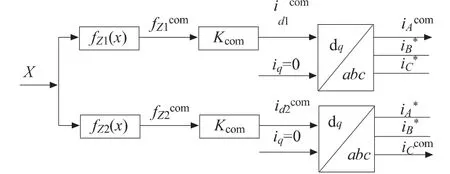
图6 A/C 相瞬时补偿电流提取模块

3 仿真与实验结果分析

3.1 Ansoft 仿真结果及分析

以一台经过电机本体优化后的12 槽11 极单层绕组永磁直线伺服电机为例进行仿真验证。电机的相关参数如表1。依据第2 节推出的A/C相电流分相补偿模型式(11)、(12)进行电流补偿，当iq=7A 时，结果如图7。

表1 电机参数

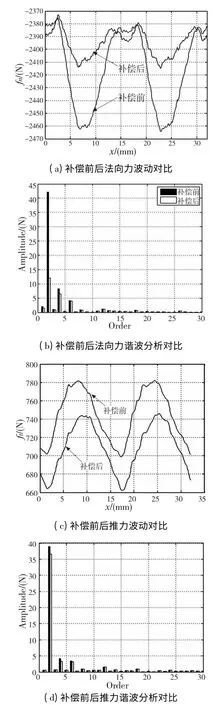
图7 11 极12 槽PMLSM 仿真结果

从图7a 可以看出注入A/C相补偿电流前后法向力均值由2415.05N 减小到2394.24N，法向力波动值由88.8N 减小到41.8N，从图7b 可以看出引起法向力波动的主要次谐波二次谐波的幅值由42. 5 减小到12.2，优化效果比较明显;同时从图7c、d 可以看出推力由743.9N 减小到708.6N，衰减4.7%，波动幅值基本不变。由此可见，这种分相电流补偿控制策略能够有效地减小PMLSM 的法向力波动，且对推力及其波动影响较小。

3.2 实验结果及分析

PMLSM 法向力波动测试系统如图8 所示。测试系统由控制单元、进给装置及检测单元组成，其中检测单元包括四个TPD505 微型荷重型测力传感器及BVM-300-4M 四通道振动测试与模态分析仪。在每根导轨下均匀安装2 个称重传感器，初级在导轨上运行时，由光栅尺和数显表测量并显示初级移动距离，由振动测试仪在测量区间采集称重传感器数据。导轨所受到的压力是直线电动机法向力和重力的合力，通过四个称重传感器的输出，间接计算出在一极距范围内永磁直线同步电动机不同位置法向力的变化。

图8 法向力测试实验平台

采用分相补偿控制策略前后，检测单元测得的法向力减去电机动子及工作台的自身重力，如图9 所示。实验结果与仿真结果存在偏差的主要原因有:①永磁体充磁不均匀，电机制造及安装上存在一定形位误差;②检测单元误差等。波形存在毛刺主要原因有:①直线电机速度环的不断调节，使电流不断微调;②四通道振动测试与模态分析仪计算法向力时存在误差。由图9 可知，有限元计算得出的法向力与实测基本符合。证明了分相补偿控制策略可以有效减小PMLSM 法向力波动。

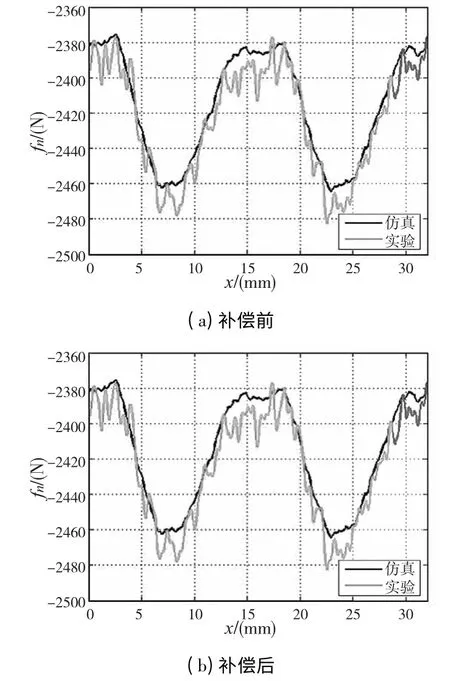
图9 PMLSM 法向力测试结果

4 结论

本文针对抑制单边平板型PMLSM 法向力波动提出了一种新颖的A/C 分相电流补偿控制策略，通过理论分析以及仿真验证，得到以下结论:

(1)经仿真结果验证，端部法向力是关于位移和电流的多维非线性周期函数，本文推导的永磁直线伺服电机A/C 相电流补偿模型能够准确的反应端部效应引起的法向力波动。

(2)采用A/C 分相电流补偿控制策略能够使法向力波动的主要次谐波二次谐波分量的幅值减小70%，且对推力及其波动影响不大，基本达到了推力不变法向力波动最小的效果。

(3)通过本文提出的分析方法确定分相电流补偿模型，也可用于抑制PMLSM 端部效应引起的推力波动。

［1］Otsuka Jiro，Hayama Sadaji. Special Issue on Precision and Ultra-precision Positioning［J］.International Journal of Automation Technology，2009，3(3):223 -226.

［2］Min-Seok Kim，Sung-Chong Chung. A systematic approach to design high-performance feed drive systems［J］. International Journal of Machine Tools ＆Manufacture.2005，45:1421–1435.

［3］夏加宽，王成元，李埠东，等. 高精度数控机床用直线电机端部效应分析及神经网络补偿技术研究［J］. 中国电机工程学报，2003，23(8):100 -104.

［4］王昊，张之敬，刘成颖. 永磁直线同步电机纵向端部效应补偿方法［J］. 中国电机工程学报，2010，30(36):46-52.

［5］Miralem H.，Viktor G.，Tine M.. Magnetic field analysis in slotless PM linear motor model:comparison of calculated and measured results［J］. Electrical Review，2011，87(3):65-69.

［6］宁建荣，夏加宽，沈丽，等. 基于有限元法的永磁直线同步电动机动子瞬态振动预测［J］. 中国机械工程，2011，22 (6):671 -674.

［7］郭瑶瑶，刘成颖，王先逵. 机床进给系统用永磁直线电机法向吸力的研究［J］.中国机械工程，2007，18(10):1174-1177.

［8］Jia-kuan Xia，Wei-yang Li，Li Shen. Skew and End-teeth optimization in Reduce Permanent magnet Linear Synchronous Motor Normal Force Fluctuation［J］. ICEEAC2010，Nov.Zibo，P.R.China，2010，6:518 -522.

［9］Mu Hai-Hua，Zhou Yun-Fei，WenXin.Calibration and compensation of cogging effect in a permanent magnet linear motor［J］，Mechatronics ，2009，19:577 -585.

［10］孙宜标，闫峰，刘春芳. 基于μ 理论的永磁直线同步电机鲁棒重复控制［J］. 中国电机工程学报，2009，29(30):52 -57.

［11］Yu-Wu Zhu，Sang-Min Jin，Koon-Seok Chung，et al. Control-Based Reduction of Detent Force for Permanent Magnet Linear Synchronous Motor［J］. IEEE TRANSACTIONS ON MAGNETICS，2009，45(6):2827 -2830.

［12］潘开林，傅建中，陈子辰.永磁直线同步电机的磁阻力分析及其最小化研究［J］.中国电机工程学报，2004，24(4):112 -115.