磁悬浮平台中开环磁路的漏磁通分析*
吴国庆,钱小磊,张旭东,孙后全
(1.南通大学 机械工程学院,江苏 南通226019;2.南通大学 电气工程学院,江苏 南通226019)
0 引言
磁悬浮平台的设计是研究各种磁悬浮加工机床的基础工作,包含悬浮系统和直线驱动系统,按作用力的方向,分为是垂直系统和水平系统。悬浮系统是一种典型的非线性控制系统[1],在实际工程中,由于平台上载荷的变化和加工刀具的切削力引起的振动等不确定因素,使得系统更为复杂。因此实现悬浮系统的精密控制需要建立较为合理的电磁力数学模型。传统的解决思路是设计工作磁路,等效成电路,文献[2]将三段气隙区域等效为三段电阻,通电线圈等效为电流源,构建了简便的磁路等效电路,并给予了实验验证,但是实验结果明显高出了理论计算值7.98%,主要因为忽略了磁铁外围的漏磁。文献[3]采用了神经网络建模研究,虽然建立了悬浮系统的动力学模型,但仅限于单向电磁铁悬浮控制,某种程度上增加了控制难度。本文采用差动励磁式的吸力型悬浮系统[4],以求获得悬浮系统中电磁力-气隙的精确数学模型。
1 磁悬浮平台气隙磁场
支撑电磁铁与导轨衔铁之间的气隙磁场对磁悬浮平台的性能有至关重要的影响,研究支撑电磁铁与导轨衔铁之间的气隙磁场对整个磁悬浮平台的设计和控制都很重要[5]。就U 型导轨(结构见图1)而言,当其气隙磁场越接近均匀分布,则其支撑磁力越平稳,平台鲁棒性越好。V 型导轨(结构见图2)气隙磁场存在法向和径向分量。法向气隙磁场成均匀分布,与支撑电流作用产生法向磁力,也就是平台的磁吸力,与平台自重平衡,达到悬浮目标;径向气隙磁场以中心线为对称轴成对称分布,产生径向力,径向力会对平台水平驱动产生横向扰动。
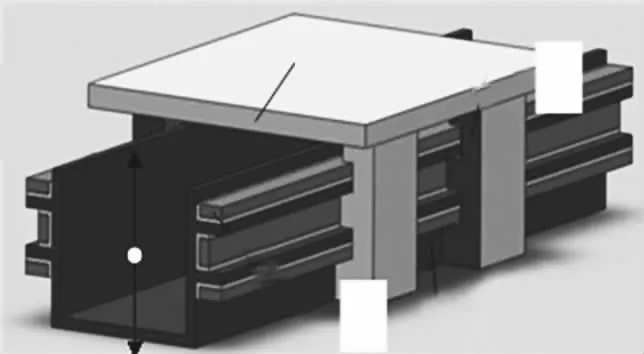
图1 U 型导轨结构图

图2 V 型导轨结构图
磁悬浮平台磁路由支撑电磁铁内部磁路、第一段气隙磁场和支撑导轨内部磁路以及第二段气隙磁场四部分组成。图3 为差动励磁式的吸力型悬浮系统的结构示意图。
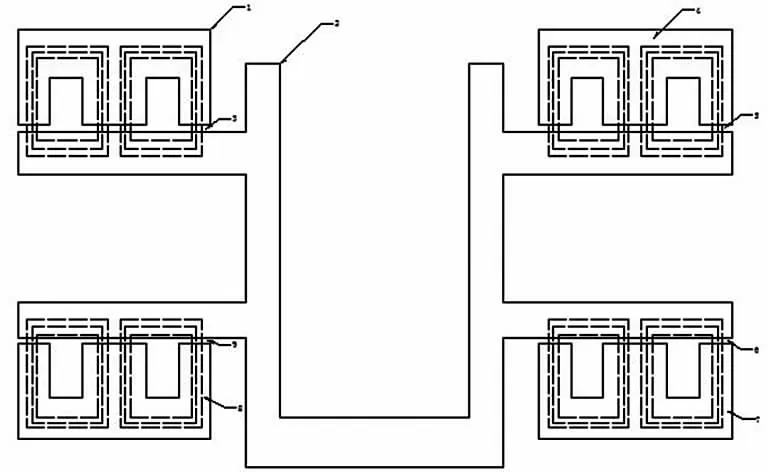
图3 差动励磁式的吸力型悬浮系统的磁路示意图
E 型电磁铁等同两个U 型电磁铁横向叠加而成,线圈绕在E 型电磁铁中间扼臂上,线圈通电后产生双回路磁路,根据平台上载荷变化的信号,实时调节控制电流值,使工作气隙稳定在一定的允许范围内。
2 磁力-气隙数学模型
2.1 E 型电磁铁选材
硅钢散热性能好,能满足所设计要求,但造价较高,加工比较困难,尤其是表面粗糙度不能满足;坡莫合金和铁氧材料都是较好的导磁材料,但是造价昂贵;碳钢造价不高且易于加工符合要求,剩磁较大,对磁悬浮工作台控制有较大影响;相对而言,纯铁导磁能力较好,造价较低,易于加工,因此,纯铁是E 型铁较理想的材料[6]。
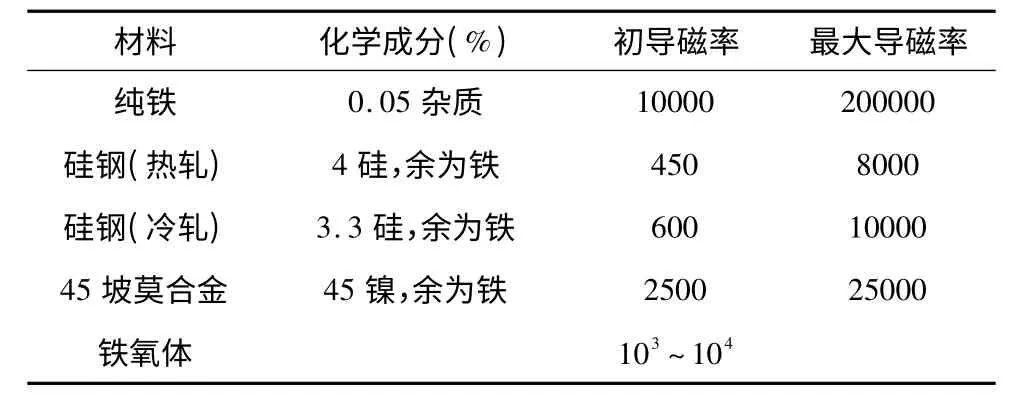
表1 几种常见软磁材料的性能
2.2 气隙-漏磁通数学模型参数的确定
μE、μg——分别是E 型铁、支撑导轨的磁导率;
μ0——空气磁导率,通常取1.256 ×10-6H/m;
δ——气隙值,预设的工作变化范围0. 25 -0.30mm
磁悬浮平台与支撑导轨采用精密的整体装配,气隙公差尺寸确定0.30-0.05mm。Agap1、Agap2气隙处工作截面积,AE和Ag分别是电磁铁扼臂截面积和支撑导轨工作段截面积。
E 型电磁铁有三段扼臂,截面积分别记为A1,A2和A3,A2=2A1=2A3。气隙有效工作区域与E 型电磁铁扼臂截面积相差无几,为简化理论计算,预设

采用漆包铜质线圈,无负载时控制电流值2A,软铁饱和磁感应强度Bm=1.62T,线圈匝数N=192,最大偏执电流I=2A,ΦE为工作段磁通量。

2.3 气隙-漏磁通数值分析
依据磁路安培环路定律:Hg、HE、Hδ分别是导轨段、电磁铁段和气隙段磁场强度,单位A/m;lg、lE、δ 分别是导轨段、电磁铁段和气隙段磁路长度,单位mm;Le是总磁路长,单位mm。

悬浮平台工作时,通入悬浮控制电流I,可认为通电线圈为磁场源。由于线圈紧密缠绕E 型电磁铁中心扼臂,类似于通电螺线管,线圈激发产生的磁场能绝大部分传递至被包裹的电磁铁,剩余磁能与发热线圈叠加作用,经过热交换散失在空气中。
由于存在一定高度的气隙,主磁通由E 型电磁铁扼臂流向工作气隙时,磁能损失较多,具体表现在漏磁通。设定磁通散失系数α,采用相同材质的铁磁材料做为E 型电磁铁和工作导轨,磁通由E 型电磁铁流向工作气隙的散失系数和磁通由支撑导轨流向工作气隙的散失系数相同。表现在直流线圈激发的主磁通未全部沿着工作扼臂流向工作气隙,称之谓扼臂散失磁通,
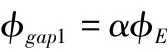
表现在主磁通未全部沿支撑导轨流向下一个工作气隙,称之谓导轨散失磁通,
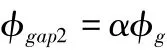
总漏磁通

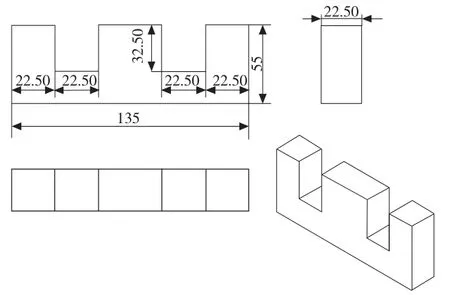
图4 设计的E 型电磁铁尺寸图
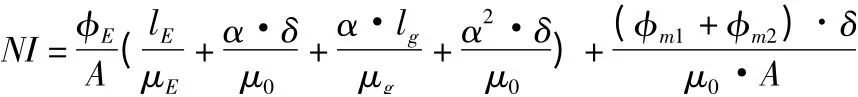
第一项为气隙工作有效磁能段,第二项为非工作散失磁能段。
比较空气磁导率和软铁磁导率,两者之间相差超过9 个数量级,即μE<<μ0,μg<<μ0,可以忽略两项。
于是

运用Matlab 软件对数学模型进行数值计算,对于气隙从0.25mm 至0.30mm 之间的变化,每隔0.05mm取点。

图5 漏磁通-气隙关系图体
E 型磁铁的吸引力产生在具有不同磁导率μ 的界面[7]上,电磁吸力的计算以磁场能量为基础,设存储在空气气隙的能量为W,则

由于V=A1·δ+A2·δ+A3·δ=4A·δ,故

对于小位移dδ,气隙内磁通Φ 保持不变,当气隙δ增加dδ 时,体积V也增加dV,而磁场能W也增加dW,由虚位移原理得吸引力F:
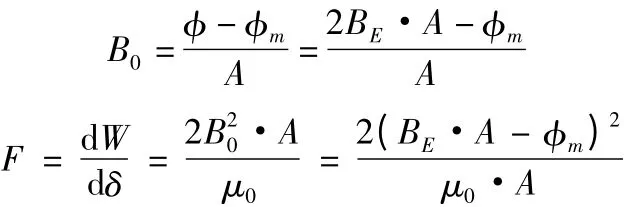
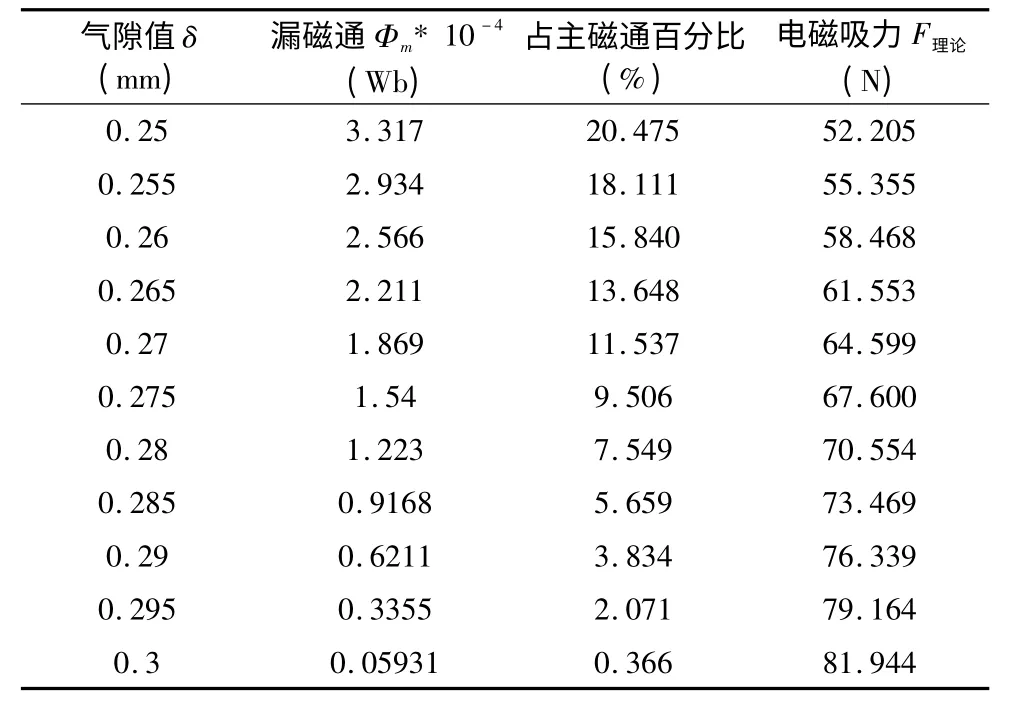
表2 气隙、理论电磁铁吸力关系
从表2 中可以看出,气隙在0.275mm 到0.3mm范围内逐次增加时,漏磁通占主磁通的百分比低于10%,气隙处磁场吸力从67.6N 增至81.944N,上升比例超过20%。表明电磁力是由气隙磁场和漏磁场共同产生的,漏磁场对电磁力也有贡献[8]。为了进一步验证建立的气隙-漏磁通数学模型的可靠性,运用有限元分析软件对该模型予以仿真计算。
3 漏磁通-气隙数学模型有限元仿真
3.1 建立三维有限元模型
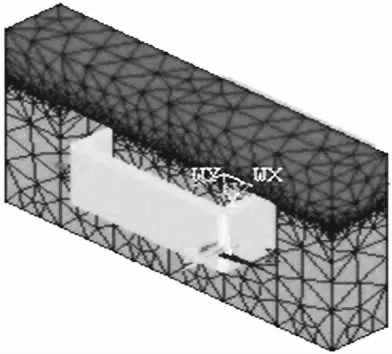
图6 E 型电磁铁三维有限元模型图
如图6 所示,电磁铁选用高磁导率的纯铁材料,纯铁磁导率大,磁滞耗低,易退磁,发热小,造价较低。其密度为7.8 ×103kg/m3,弹性模量为206Gpa,泊松比η=0.3。支撑导轨选用球墨铸铁。
3.2 计算结果及分析
通电线圈是系统的磁场源,在材料描述中已经对它的磁特性进行了定义,有限元法在处理通电线圈时自动将其转化为等效电流并加载到每个单元和节点上。对剖分后的有限元模型进行加载求解,对求解结果进行分析,得如图7 所示的三维模型的磁通密度矢量图。
由图8 可以看出,磁力线大部分穿过由E 型电磁铁扼臂、气隙和支撑导轨组成的磁回路,而在气隙附近磁通密度明显稠密,且存在漏磁现象,说明开环磁路系统漏磁存在的必然性。
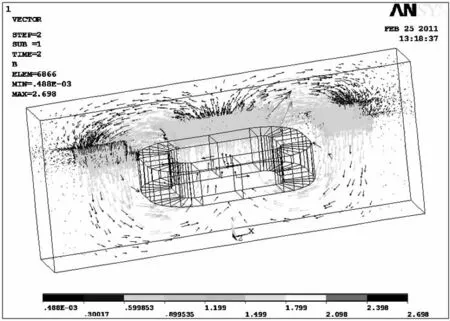
图7 E 形电磁铁三维磁通密度矢量图
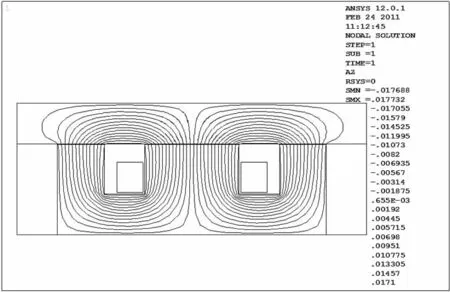
图8 E 形电磁铁二维磁力线分布图
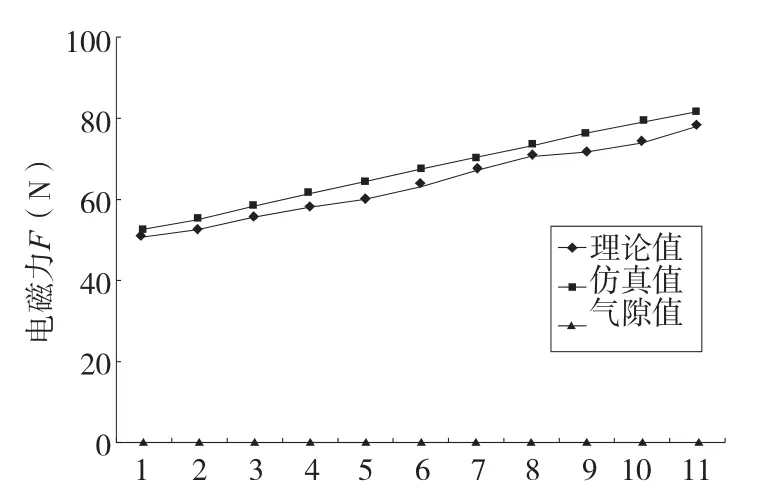
图9 电磁力理论计算结果与仿真结果对照图
由图9 可知,根据建立的数学模型求出的理论电磁力略大于仿真实现的结果,在气隙值为0. 295mm时,仿真结果低于理论值约5.23%,达到最大变化范围。经分析认为,在整个仿真过程中,设置的电磁铁和支撑导轨的导磁率为固定值,不符合磁悬浮平台实际工作情况,磁悬浮平台样机的电磁铁选用纯铁材料,支撑导轨选用球墨铸铁材料,材料本身的导磁率存在一个变化范围,受线圈直流大小变化的影响,这种变化是非线性的。图8 中二维漏磁场[9]仿真显示的信息仅是整个磁路的正视剖面图,而图7 三维漏磁场仿真显示了整个磁路空间的漏磁信息,改变了电磁力的仿真值。因此如何有效的增加二维磁场仿真和三维磁场仿真之间的联系是进一步研究漏磁通影响的关键。
4 结论
在磁悬浮平台的开环磁路中,建立漏磁通-气隙数学模型并通过有限元仿真验证,确定了漏磁通的存在,侧重从气隙角度控制漏磁通的影响,实现了对漏磁通和电磁力之间关系的研究,借鉴改进后的数学计算模型,可以为磁悬浮平台样机以后的调试工作提供实际参考价值。
[1]石佳. 机床进给磁悬浮系统的非线性控制方法研究[D]. 沈阳:沈阳工业大学,2008.
[2]兴涛,杨建波,郭永献. U 型磁铁磁路分布与气隙磁感应强度[J]. 机械设计与制造,2008(7):82 -83.
[3]Longxue Xiao,Guoqing Wu,Xudong Zhang. Modal Analysis of Maglev Linear Feed Unit. Applied Mechanics and Materials,2012,150:205 -211.
[4]黄毅. 基于dSPACE 的磁悬浮运动平台控制方法研究[D]. 长沙:中南大学,2009.
[5]Jaewook Lee,Ercan M. Dede and Tsuyoshi Nomura. Simultaneous Design Optimization of Permanent Magnet,Coils,and Ferromagnetic Material in Actuators. IEEE TRANSACTIONS ON MAGNETICS,2011,47(12):4712 -4716.
[6]Wohlfarth. 铁磁材料:磁有序物质特性手册第二版[M].北京:电子工业出版社,1993.
[7]肖龙雪. 磁悬浮直线进给单元结构设计[D]. 南通:南通大学,2011.
[8]纪凤珠,王长龙,陈正阁,等. 基于三维有限元法的漏磁场分析[J]. 兵工学报,2007,28(7):876 -879.
[9]Lee J Y,Lee S J ,Jiles D C ,et al. Sensitivity analysis of simulations for magnetic particle inspection using the finiteelement method. IEEE Transactions on Magnetics,2003,39(6):3604 -3606.

