机载武器发射系统刚柔耦合动力学仿真

王许可

(中国空空导弹研究院科技部，河南洛阳471009)

机载武器发射系统刚柔耦合动力学仿真

王许可

(中国空空导弹研究院科技部，河南洛阳471009)

为了研究某空空导弹内埋弹射发射系统结构参数对其发射分离参数的影响，针对多刚体模型不能准确仿真发射过程中发射俯仰角速度存在强烈柔性波动效应的问题，基于刚柔耦合多体动力学理论，建立了某空空导弹发射系统刚柔耦合动力学仿真模型;采用该模型对发射系统的导弹发射分离参数进行仿真，详细讨论了导弹重心、弹射发射行程、结构刚度等设计参数对导弹发射分离角速度的影响;发现导弹重心位于垂直作动筒作用点后，4根同步杆和4个转动臂需保证较好的刚度，且发射行程不超过350 mm时，导弹弹射分离角速度不会产生抬头效应，发射安全性较好。

柔性动力学;内埋弹射;俯仰角速度;导弹发射系统;发射动力学

从20世纪80年代以来，美国和俄罗斯都陆续开始了新一代战斗机的研制，如美国的F－22、JSF计划和俄罗斯的MFI计划。为了达到新一代战机隐身和超音速巡航的目的，四代机携带的空空导弹武器均采用内埋弹射发射方式，并要求发射过程极其迅速，不影响飞机的隐身特性。美国的F－22A采用LAU－142/A弹射发射装置发射导弹，其发射AIM－120C的弹射行程仅为230 mm，从发送发射指令到导弹完全分离时间仅为约0.1 s左右，内埋发射系统以40 G的力将导弹以8.2 m/s的速度弹出内埋武器舱，使导弹快速离开机身的扰动区，保证发射时载机的安全性［1］。对于机载内埋弹射发射系统，弹射分离俯仰角速度对导弹发射安全性具有重要影响，若出现抬头角速度，则很可能产生机毁人亡的严重事故。在此对某空空导弹内埋弹射发射系统动力学特性进行分析，保证机弹分离的发射安全性，对我国在相关技术领域开展工作具有指导意义。

1 刚柔耦合动力学理论基础

多体系统既存在构件大范围的刚体运动，又存在弹性变形［2］，因而刚柔耦合系统动力学与多刚体系统动力学及结构有限元分析均有密切关系。刚体可以按多刚体系统动力学理论建立方程，柔性体可以用有限元法建立方程，将两者组集就可得到刚柔耦合的多体系统的动力学方程。

本文所讨论的刚柔耦合动力学数学模型基于第一类拉格朗日方程进行动力学求解［3］:

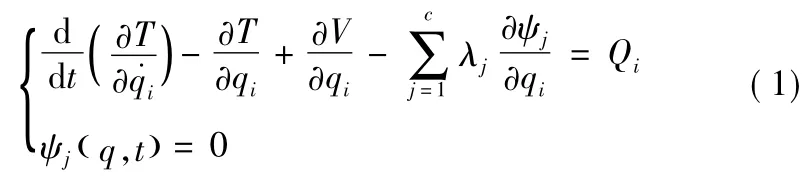
式(1)中:ψj为约束方程;λj为拉格朗日乘子向量;qi为柔性体的广义坐标;T为构件的动能;V为柔性体的势能;Qi为施加的广义力。

在柔性体内，由变形引起的弹性力的虚功为

K为对应于柔性体广义坐标q的刚度矩阵。

对应于广义坐标的构件的动能为:

式(3)中，M为构件的质量矩阵。

将式(2)和式(3)代入式(1)得到:

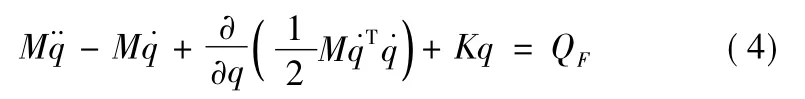
式(4)中，Kq为弹性力对应的广义力，QF为作用于柔性体上除变形引起的弹性力以外的全部主动力对应的广义力。

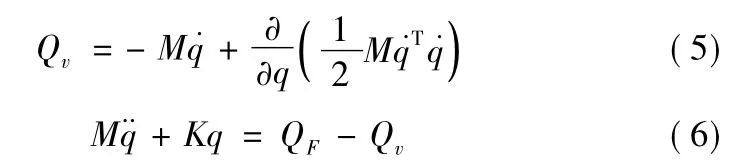
加以相应的约束方程，则用拉格朗日乘子法建立的刚柔耦合动力学方程为

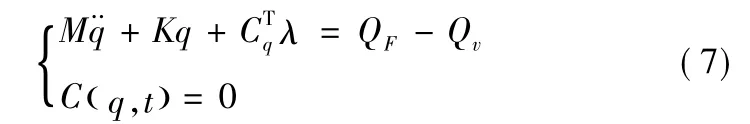
式(7)中，Cq为C( q，t)=0的雅各比矩阵，CTqλ为作用于柔性体上的广义力。

2 发射系统刚柔耦合动力学模型建立

2.1 系统总体组成

某机载弹射发射装置主要由垂直作动筒、上下梁、4根同步杆和4个转动臂等组成。弹射导弹时，垂直作动筒在气体压力作用下推动下梁向下运动，同时4个转动臂展开，保证下梁平稳的向下运动，而4根同步杆保证前后4个转动臂同步展开。其总体组成如图1所示。

图1 某导弹发射系统总体组成

2.2 动力学模型建模

机载武器内埋弹射发射装置发射时具有瞬时大过载的工作特性，并且发射装置的同步杆属于细长杆类型，因此必须考虑结构的柔性效应对发射分离姿态的影响，尤其是对导弹分离角速度的影响。在建模过程中，对前后4个转动臂、左右4根同步杆进行柔性化处理，上梁和下梁由于刚度较大，不做柔性化处理。

各构件动力学拓扑关系为

上梁:与“大地”固结，作为整个发射系统的固定基础;

前上转动臂:与上梁装配为轴旋转约束，与前下转动臂装配为轴旋转约束;

前下转动臂:与前上转动臂装配为轴旋转约束，与下梁装配为轴旋转约束;

后上转动臂:与上梁装配为轴旋转约束，与后下转动臂装配为轴旋转约束;

后下转动臂:与后上转动臂装配为轴旋转约束，与下梁装配为轴旋转约束;

4根同步杆:4个同步杆其两端与其连接的转动臂均为轴旋转约束;

垂直作动筒:与上梁装配为轴旋转约束关系，与下梁装配为轴旋转约束关系，垂直作动筒内部为活塞沿垂直作动筒壁滑动。

3 动力学仿真分析

3.1 柔性化仿真处理方法

由于某机载武器发射系统具有弹射力大且柔性杆多的特点，刚性模型不能仿真其分离速度和分离角速度的柔性波动效应，因此必须采用柔性化模型对弹射分离姿态进行动力学仿真。另外柔性化处理中可能存在柔性化不足或者过度柔性化的问题，因此对4个转动臂、4根同步杆作模态试验和拉伸试验，通过试验数据修正4个转动臂、4根同步杆的柔性化模型，直到其柔性仿真模型与试验结果基本一致，最后建立发射系统整机动力学仿真模型。柔性化处理思路和步骤如图2所示。

图2 柔性动力学仿真流程

3.2 仿真结果分析

导弹发射分离速度和分离角速度是发射系统主要的发射分离性能参数。分离速度决定了导弹脱离载机的快慢，分离速度小，脱离载机时间长，导弹在气动力作用下可能影响载机安全。分离角速度对发射安全性具有非常重要的影响，若分离角速度为正值或接近0值即出现“抬头”角速度，导弹在气动力作用下将出现导弹向上飞并与飞机相撞的危险［5］，因此必须避免角速度“抬头”。

从图3可以看出:某机载发射系统从弹射开始到导弹与发射架分离时间约为60 ms，弹射分离速度约为8.3 m/s。

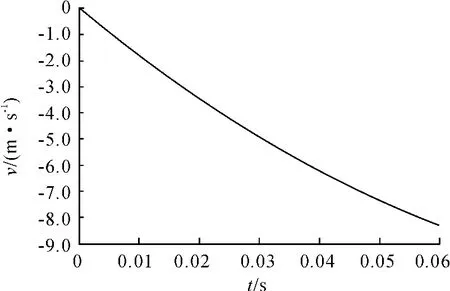
图3 导弹弹射分离速度曲线

曲线1为刚柔耦合模型俯仰角速度仿真曲线;曲线2为多刚体模型俯仰角速度仿真曲线。从图4中可以看出:刚柔耦合模型相对于多刚体模型其仿真角速度曲线具有非常大的差别。多刚体模型仿真曲线其俯仰角速度一直向下，其“低头”值越来越大，而刚柔耦合模型仿真曲线其俯仰角速度先迅速“低头”，在发射行程中点附近却迅速“抬头”，出现严重影响发射分离安全性的角速度“抬头”现象。

通过实物样机试验证明，刚柔耦合模型仿真的俯仰角速度与试验俯仰角速度非常接近。可以说明某发射系统在发射过程中具有较强的柔性弹性效应，多刚体仿真模型不足以模拟其发射动力学特性。

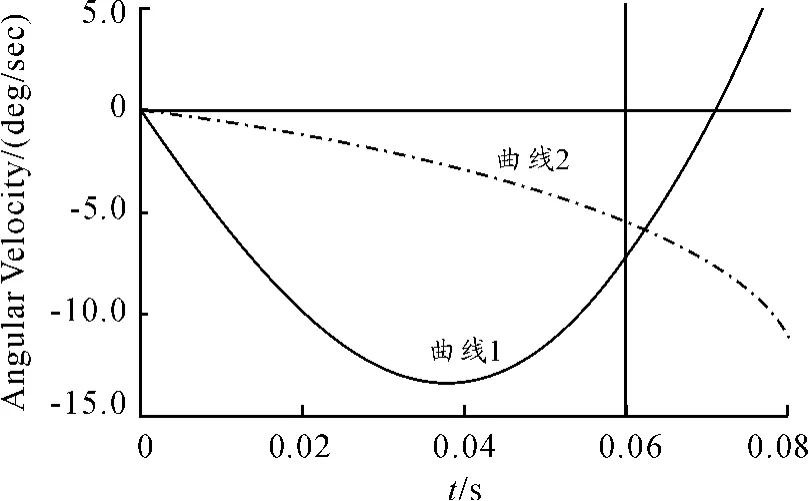
图4 导弹发射俯仰角速度

3.3 设计参数对发射俯仰角速度的影响

发射俯仰角速度对发射安全性具有非常重要的影响，导弹若出现抬头的角速度或角度，导弹与发射系统分离后在气动力作用下则可能出现导弹与飞机相撞最后机毁人亡的严重事故。为了保证导弹发射时机弹分离安全性，导弹发射俯仰角速度和发射俯仰角度均需要保证一定的低头值［6］。

3.3.1 导弹重心对发射俯仰角速度的影响

取3种状态仿真:导弹重心在垂直作动筒前100 mm(曲线qian_100 mm);导弹重心在垂直作动筒正下方(曲线0 mm);导弹重心在垂直作动筒后100 mm(曲线hou_100 mm)。

从图5中可以看出，当导弹重心处于垂直作动筒作用点前100 mm时，导弹在发射过程中由于垂直作动筒相对于导弹重心施加了一个抬头力矩，因此角速度先是抬头，后来由于结构柔性效应的回弹作用，角速度抬头值逐渐减小，但是整个过程中导弹角度始终处于抬头状态，因此，导弹重心处于垂直作动筒作用点前存在严重发射安全隐患。

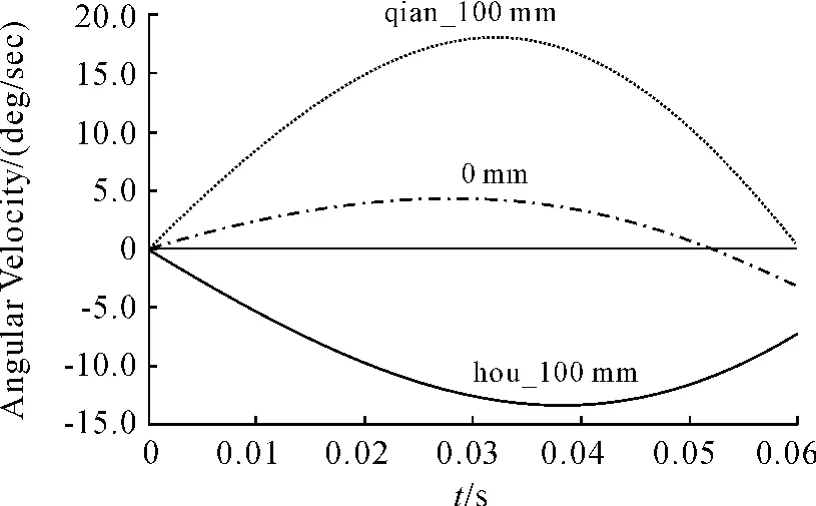
图5 导弹发射俯仰角速度曲线

当导弹重心处于垂直作动筒作用点正下方时(0 mm)，虽然垂直作动筒并没有对导弹施加额外俯仰力矩，但是在机构柔性效应影响下导弹也存在一定的角速度波动，但是波动值较小，发射角度基本处于0°左右，也不能可靠保证导弹发射安全性。

当导弹重心位于垂直作动筒作用点的后100 mm时，导弹发射时垂直作动筒给导弹施加了一个低头力矩，因此角速度先是低头，后来由于结构柔性效应的回弹作用，角速度低头值逐渐变小，若控制好机构的刚性以及弹射分离点，能够保证导弹发射时角速度和角度均处于低头状态。因此导弹重心处于垂直作动筒作用点之后一定距离有利于发射安全性。

3.3.2 发射行程对俯仰角速度的影响

从图6和图7中可以看出，当分离点在约230 mm时，其弹射作动时间是约60 ms，分离角速度是－7.3 deg/s，其角速度和角度均处于低头状态，当有约束发射行程在350 mm时，此刻角速度由低头状态转为抬头状态，存在发射安全隐患，当有约束发射行程大于350 mm，角速度为抬头状态，存在严重发射安全性问题，因此有约束发射行程不能大于350 mm。

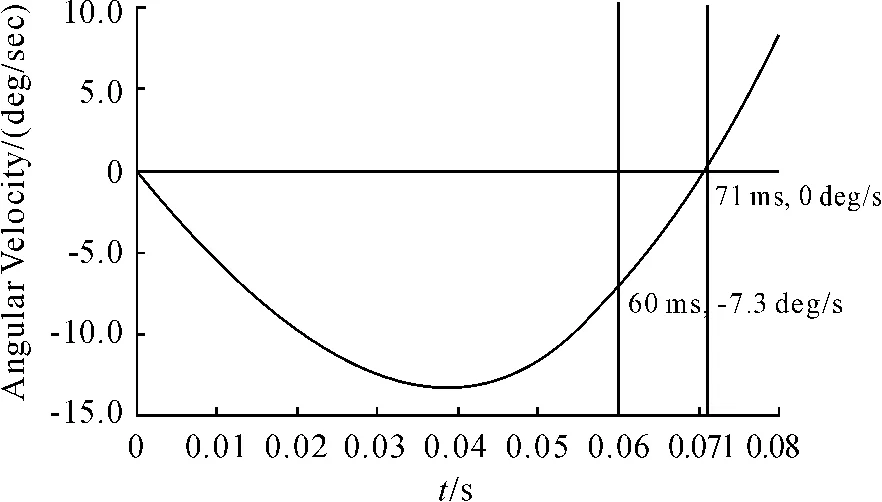
图6 导弹俯仰角速度曲线

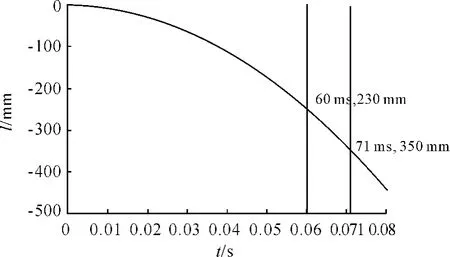
图7 导弹竖直方向位移曲线

3.3.3 柔性效应对发射角速度和角度的影响

某内埋弹射发射装置发射过程中作用力较大，并且为了保证发射系统具有较低的重量，各杆件设计刚度较低，因此系统的柔性特性比较强烈。本模型对4个转动臂，4根同步杆进行了柔性化处理。

曲线1:多刚体模型俯仰角速度曲线;

曲线2:4根同步杆为柔性体，其他为刚体状态下的俯仰角速度曲线;

曲线3:4个转动臂为柔性体，其他为刚体状态下的俯仰角速度曲线;

曲线4:4个转动臂和4根同步杆均为柔性体状态下的俯仰角速度曲线。

从图8中可以看出:多刚体模型(曲线1)的俯仰角速度低头值不断线性增大，且一直处于低头状态。

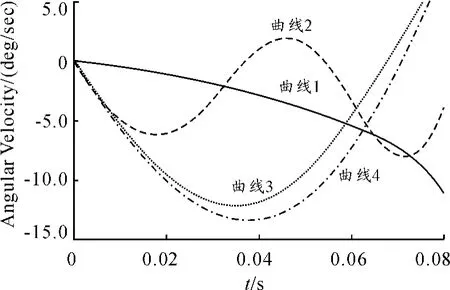
图8 导弹弹射俯仰角速度曲线

当4个同步杆作为柔性体仿真时(曲线2)，其角速度曲线绕刚体模型角速度曲线波动，且波动幅度很大，角速度状态不稳定，因此，4个同步杆的刚度直接影响发射系统的发射时角速度的稳定性，因此设计时须保证同步杆的刚度。

4个转动臂为柔性体仿真时(曲线3)，角速度波动幅度更大，如果弹射行程大于一定值时，其角速度甚至可能出现稳定的抬头值，不利于发射安全性，必须避免。

4个转动臂和4根同步杆均为柔性体时仿真角速度曲线(曲线4)与曲线3比较接近，角速度会出现一个较大的由低头到抬头的波动，当弹射行程大于一定值时(350 mm)，出现稳定的抬头现象，严重影响发射安全性，必须避免。

因此，在某发射系统设计时须控制好4个转动臂和4根同步杆的刚度，且限制发射行程不超过350 mm，否则将出现“抬头”角速度，严重影响载机安全。

4 结论

1)某机载武器内埋弹射发射系统在发射过程中俯仰角速度存在非常强的柔性效应，多刚体仿真模型不足以仿真其发射动力学特性;

2)本文采用的通过模态试验和拉伸试验修正关键部件柔性化有限元模型，最后修正整机动力学模型的仿真方法具有较高的仿真精度，能够分析各重要设计参数对发射动态特性的影响;

3)导弹重心须处于垂直作动筒作用点之后，且发射行程不能过大(350 mm)，否则导弹将出现较强的角速度抬头效应，严重影响发射安全性;

4)4根同步杆和4个转动臂需保证较好的刚度，否则导弹发射分离角速度具有较大的波动，甚至出现角速度抬头现象，影响发射安全性。

［1］张士卫.弹射装置刚柔耦合动力学分析［J］，科学技术与工程，2010，10(22):5456－5460.

［2］蒋丽忠、赵跃宇.作大范围运动柔性结构的耦合动力学［M］.北京:科学出版社，2007.

［3］洪嘉振.计算多体系统动力学［M］.北京:高等教育出版社，1999.

［4］逯运通，宋顺广，王春洁，等.基于刚柔耦合模型的月球着陆器动力学分析［J］.北京航空航天大学学报，2010，36(11):1348－1352.

［5］樊会涛.空空导弹系统总体设计［M］.北京:国防工业出版社，2007.

［6］廖志忠.空空导弹发控系统设计［M］.北京:国防工业出版社，2007.

［7］陈宝，李灿，刘圣坤，等.含橡胶衬套的后悬架柔性扭力梁结构优化［J］.重庆理工大学学报:自然科学版，2012 (2):6－10.

［8］王松超，王惠方，于存贵.某多管火箭炮支撑动力学分析［J］.兵工自动化，2012(3):24－26.

［9］王林鹏，王汉平，杨鸣，等.复杂空间机构热态刚柔耦合多体动力学建模［J］.四川兵工学报，2013(9)::78－81.

(责任编辑周江川)

Dynam ical Simulation of Airborne Eject Launcher Relating to the Coup ling of Rigidity and Flexibility

WANG Xu－ke
(Department of Science and Technology，China Airborne Missile Academy，Luoyang 471009，China)

In order to study the influence of structure design parameters of air－to－airmissile buried eject launcher to launching separation parameter，multi－rigid－body system cannot simulate the problem that the pitching angular velocity has high volatility during launching.Based on the rigid－flexible coupled multibody dynamics theory，an air－airmissile launcher system dynamicsmodelwas established and used to analyze the launcher system dynamics characteristic.This paper focuses on analyzing the infection of important design parameter tomissile launch separate angle speed，including the center ofmissilemass，launch distance，and machinery rigidity.Results show that，the center ofmissilemassmustbehind vertical actuator，synchronous connecting rod and rotor arm must have enough rigidity，the launching distancemust beyond 350 mm.

flexible dynamics;buried eject launcher;separate pitching angle speed;missile launch system;launch dynamics

:A

1006－0707(2014)07－0009－05

format:WANG Xu－ke.Dynamical Simulation of Airborne Eject Launcher Relating to the Coupling of Rigidity and Flexibility［J］.Journal of Sichuan Ordnance，2014(7):9－12.

本文引用格式:王许可.机载武器发射系统刚柔耦合动力学仿真［J］.四川兵工学报，2014(7):9－12.

10.11809/scbgxb2014.07.004

2013－10－27

王许可(1983—)，男，工程师，主要从事红外制导武器系统及发射装置研究。

TJ393