改进的Rao－Blackwellized粒子滤波算法在目标跟踪中的应用

张万里，何金刚，赵红梅

(1.中国空空导弹研究院，河南洛阳471009; 2.中国航空工业集团公司洛阳电光设备研究所，河南洛阳471009)

改进的Rao－Blackwellized粒子滤波算法在目标跟踪中的应用

张万里1，何金刚1，赵红梅2

(1.中国空空导弹研究院，河南洛阳471009; 2.中国航空工业集团公司洛阳电光设备研究所，河南洛阳471009)

在雷达信号处理领域，运动目标跟踪问题一直是研究的重点，涉及的非线性滤波问题是难点所在;以Rao－Blackwellized粒子滤波(RBPF)算法为基础，针对其应用于雷达目标跟踪时产生的若干问题进行研究，为提高算法的收敛性能及滤波精度，对其中重采样算法进行改进，利用数字仿真对更改后的算法进行验证，经过表明更改后的RBPF算法在各个方面均有较大程度改善。

粒子滤波;RBPF算法;雷达目标跟踪;重采样

在雷达信号处理领域，如何实现精确的运动目标估计与跟踪，一直是长期以来的研究的重点所在。20世纪60年代已证明在线性高斯系统中利用最小均方根误差准则进行目标状态估计的Kalman滤波方法［1］是最优的估计方法，但针对非线性非高斯系统，尽管采用局部线性化近似的扩展Kalman滤波(Extend KF，EKF)［2］以及确定性采样的Unscented卡尔曼滤波(Unscented KF，UKF)［3］方法可以解决一定形式的弱非线性，弱高斯条件下的目标跟踪问题，但由于其对动态模型的限制过强，在实际应用中大多无法满足应用前提，20世纪90年代出现了以粒子滤波(Particle filter，PF)［4］为代表的非线性滤波方法，即利用蒙特卡罗采样得到的随机样本(也称为粒子)的加权和来近似状态的整个后验概率密度，其本质是采用蒙特卡罗仿真来获得高维积分的近似数值解，并用以解决各种估计问题。

粒子滤波面临实践中面临两个最大问题，一是粒子退化问题，即经过若干次迭代后，重要性权值可能集中到少数粒子上，这些粒子已经不能有效表达后验概率密度函数，为解决此问题，Gordon等［5］提出了重采用方法，其思想是减少权值较小的粒子数，增加权值较大的粒子数。另一个问题是采用粒子数目过多导致计算的复杂度增加，当前的解决方法主要是从系统模型出发，利用模型自身的特性来提高滤波器性能。Rao－Blackwellized方法［6］即将线性状态从系统中分离出来，利用Kalman滤波器对线性状态进行估计，利用粒子滤波对剩余的非线性状态进行估计，后基于贝叶斯定理求取状态的后验概率。由于RBPF降低了粒子滤波状态的维数，与使用相同粒子数的传统PF算法相比，可以获得更优的性能。

当前的Rao－Blackwellized粒子滤波(RBPF)中的重采样虽然可以一定程度上缓解权值退化的现象，但同样也会带来粒子贫化的问题;同时采用单一系统模型作为Rao－Blackwellized粒子滤波中近似线性状态的估计，在跟踪机动目标时与真实飞行轨迹存在偏差，因此为解决此类问题，本文采用权重分区并实施改进的重采样算法的方法在大权值与小权值粒子之间对权重重新计算以获取新粒子，从而实现粒子状态的估计，同时以仅有角度信息的雷达双目标跟踪问题为例，对改进的算法进行验证。

1 Rao-Blackwellized粒子滤波算法

1.1 粒子滤波算法原理

解决目标跟踪问题的最优方法是贝叶斯滤波方法，它通过两个步骤来实现:状态预测和状态更新。贝叶斯滤波的实质是通过获得目标的后验概率密度，根据某些准则(如最大后验估计)近似地计算出目标状态值。定义系统模型如下:

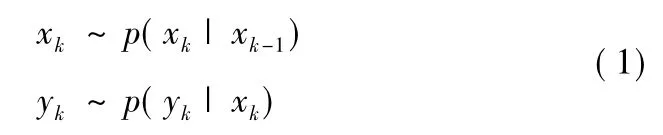
其中xk为目标在k时刻的状态，如目标的位置、速度、加速度等信息。yk为k时刻的测量值，如目标的位置、弹目距离、目标与传感器的相对角度等。p(xk|xk－1)为目标的动态模型，表征目标状态的动态变化情况，p(yk|xk)为系统的测量模型，表征目标在干扰情况下的测量变化情况。最优滤波的目的就是为了在已知观测信息z1:k的前提下获得目标的后验概率p(xk|z1:k)。

利用Chapman－Kolmogoroff公式可得目标的后验概率密度为

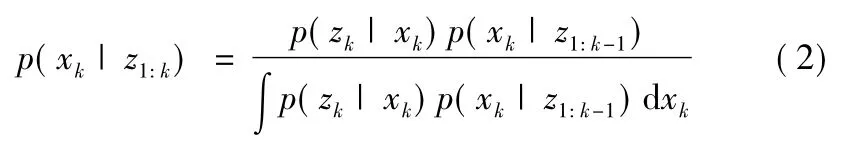
式(2)从理论意义上提供了最优滤波问题的解决方法，但在非线性系统求解过程中无穷维积分的运算极为困难，无法得到其精确最优解。

1.2 Rao-Blackwellized粒子滤波算法流程

在Rao－Blackwellized粒子滤波算法中，引入任意潜在变量λ，系统的动态模型和测量模型分别变为p(xk|xk－1，λk－1)和p(yk|xk，λk)，已知重要性分布为π)，对当前粒子群进行处理，其中m为均值，P为协方差，ω为粒子权重，N为粒子数。在K时刻，Rao－Blackwellized粒子滤波算法的流程如下:

1)对粒子均值m和协方差P做卡尔曼滤波预测:

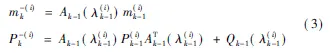
2)根据相应的重要性分布，更新潜在变量λ(i)k:

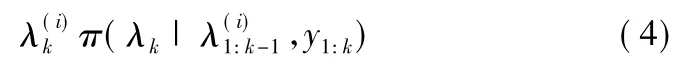
3)计算新的权重:

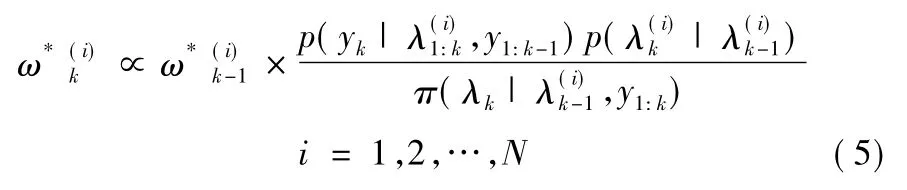
4)归一化权重:

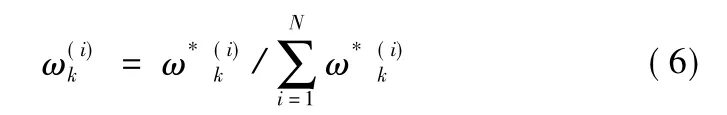
对粒子均值m和协方差P做卡尔曼滤波更新:

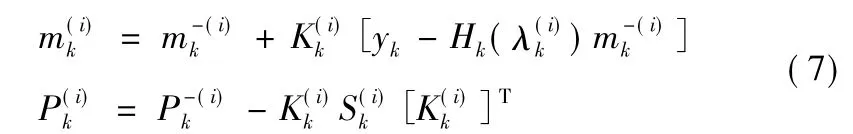
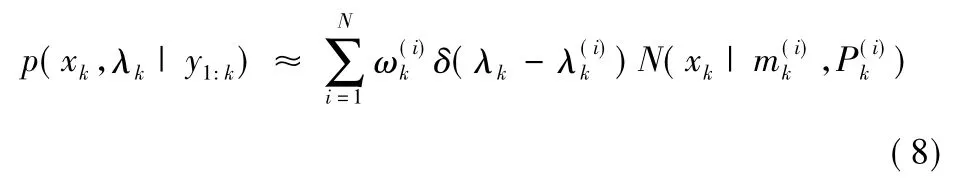
利用RBPF算法可将多目标跟踪问题分为两个部分:多目标数据关联中后验概率分布的估计和基于数据关联单个目标跟踪的估计。可以分别通过序列重要性采样及Kalman滤波进行最小均方误差估计来解决，将跟踪过程简化为目标判别，即判别当前得到的测量值是目标还是杂波，并在此基础上对目标进行跟踪。

通过设定数据关联指标Ck，当Ck=j时表示当前测量值对应第j个目标，当Ck=0时表示当前测量值经判别为杂波。

为使用RBPF滤波算法，必须首先确定一个重要性分布用以计算不同时刻k各个粒子的权值，即确定分布π(ck|，利用贝叶斯公式可以方便求取概率密度p(ck|)，因此RBPF算法默认将p()作为最优的重要性分布π来计算。

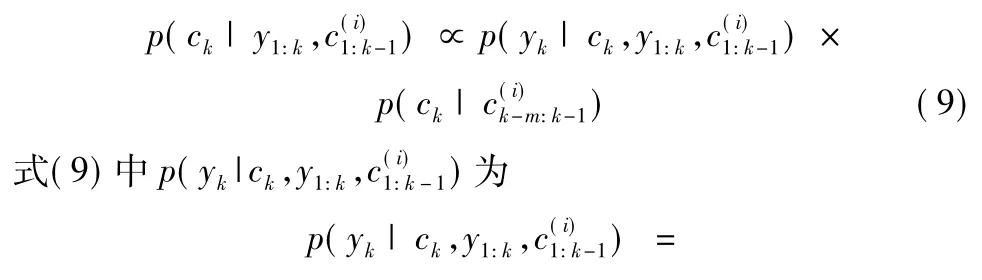
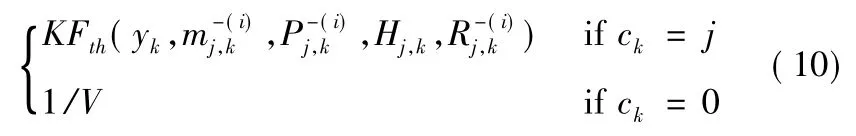
2 RBPF算法改进

在采用RBPF算法解决雷达目标跟踪问题时，发现了当前算法存在的一系列问题，包括重采样算法导致粒子贫乏性增加以及EKF或UKF算法导致预测精度较低等等，严重可能导致滤波算法发散，为此本文对以上算法进行适应性改进，以适应雷达目标跟踪问题更好的解决。

RBPF算法重采样的目的是为了缓解权值退化现象，即避免在权重较小的状态处散步同样概率的粒子数目导致计算复杂度增加的问题，其本质是以牺牲粒子多样性来减小计算量和提高鲁棒性，但通过若干次迭代可能会导致重要性权值集中到少数粒子上，这样当目标机动时状态变化频繁，此时可能导致粒子贫化进而滤波无法收敛到目标实际的状态。在利用RBPF算法针对双目标跟踪问题进行仿真时发现，常常出现滤波算法发散的情况，经分析此问题为重采样导致粒子贫化所致。

为解决此问题需在重采样时适当增加粒子的多样性，可采用改进的重采样算法，即改变重采样后权重的分配方式，这样处理虽然可能增加一定的计算量，但同时会很大程度上避免粒子贫化的问题。具体的计算步骤如下:

1)首先按照重采样前的权重将粒子分为高、中、低权重3个域，对于中权重域的粒子直接保留，为保证粒子的多样性，对低、高权重域的粒子重新分配。

2)假设低、中权重的粒子共有n个，将这两个域的权重重新归一化后，得到新的权重，计算这两个域粒子归一化后的权重加权和:

其中［］代表小数的取整部分。

3)重采样之后的低、高权重的新的权重计算如下:

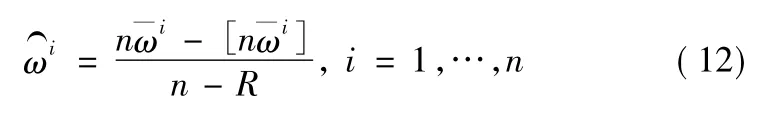
改进的重采样的算法相比当前的重采样的算法在保留中权重对粒子影响的基础上，能够适当增加小权重粒子的比例，不会像原始重采样算法那样降低粒子的多样性，当目标实施机动状态突变情况下提高滤波跟踪的可靠性，能够有效地避免滤波算法发散。

3 仿真实现

3.1 单目标跟踪的数字仿真实现

首先以杂波环境跟踪独立目标的情况进行分析，系统的状态为目标的两维位置与速度，即:

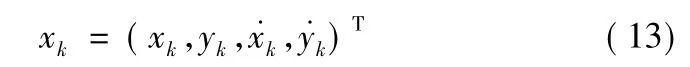
其离散化的状态方程为

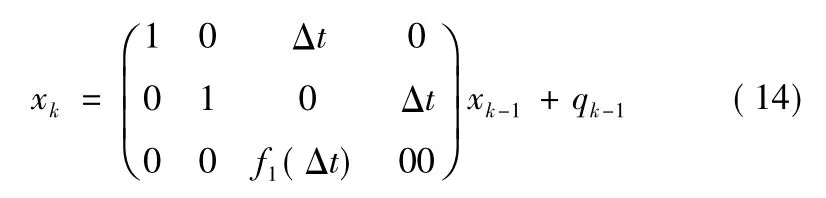
其中qk－1为离散高斯过程噪声。f1(Δt)、f2(Δt)描述目标在X向和Y向速度的变化情况。

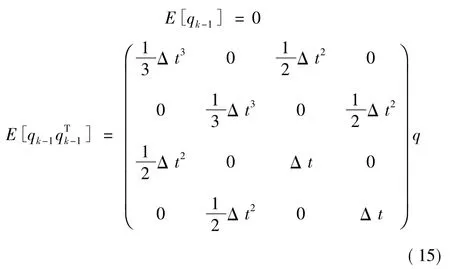
然后针对杂波环境进行建模，可杂波测量值建模为视场范围内任意随机值，由于是针对于单目标跟踪的问题，因此数据关联因子ck为0和1两种状态。且:

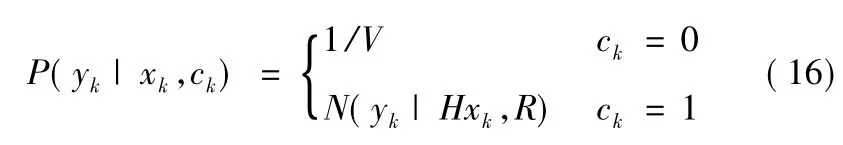
下面针对此问题分别采用线性Kalman滤波及RBPF粒子滤波来仿真，采用粒子数目为10。从图1可以看出，采用kalman滤波得到的目标运动轨迹输出完全不能够跟踪上目标的真实运动轨迹，这是因为目标的观测模型中不止存在高斯噪声，而是在整个视场内存在均匀散步的杂波测量值，这样导致Kalman滤波算法很快失效。

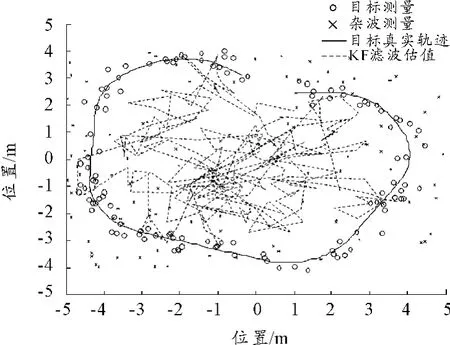
图1 采用Kalman滤波的估计结果

图2 ～图4给出了采用RBPF粒子滤波的结果，从图中可见，粒子铝箔可以较好的分辨出目标运动轨迹及杂波，并通过数据关联参数表示出来。

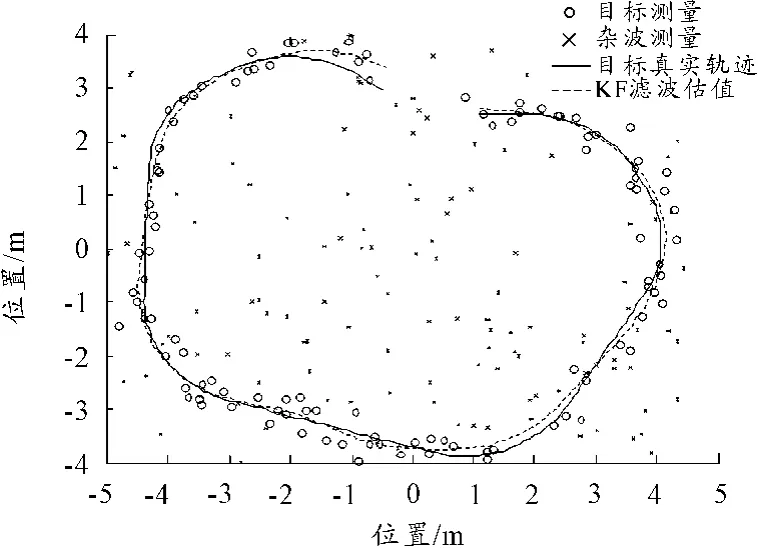
图2 粒子滤波得到的目标运动轨迹

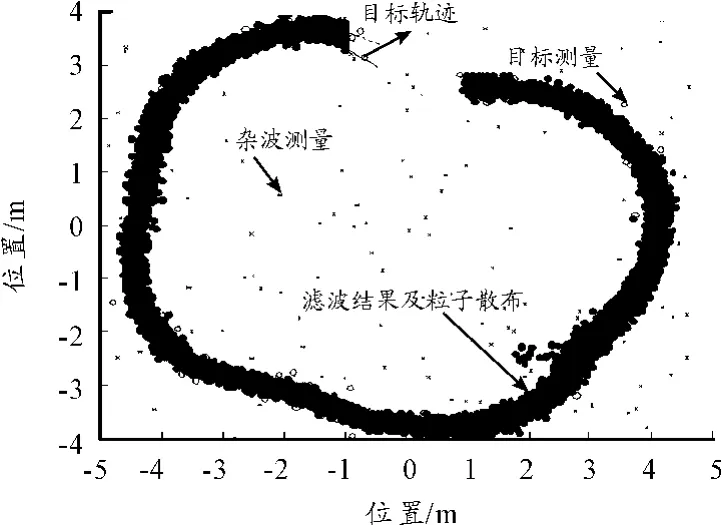
图3 粒子滤波得到的目标运动轨迹及粒子散布情况

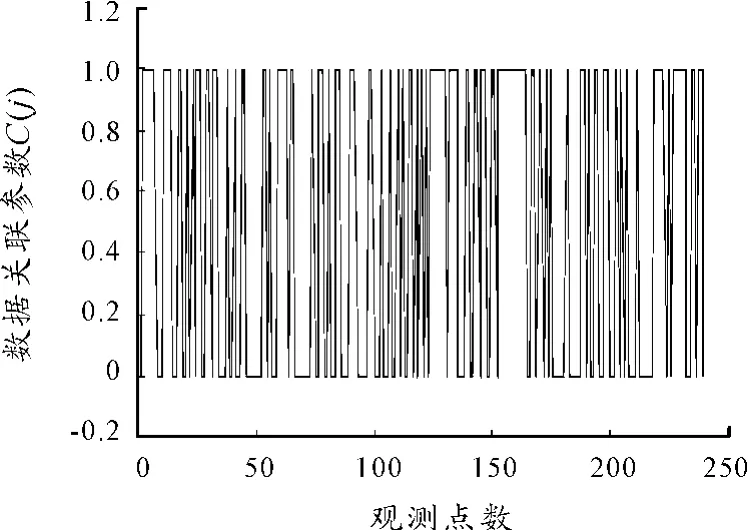
图4 数据关联参数ck

3.2 双目标跟踪的数字仿真实现

下面对仅有方位角测量信息的雷达双目标跟踪问题进行仿真验证，图5为雷达测量的示意图，此时目标的动态方程与上例中相同，但测量模型不同，此时测量量为角度值，使用两个固定位置的传感器对于两个目标进行测量，测量方程如下:

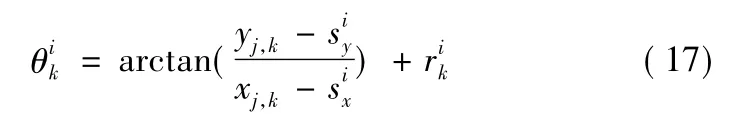
其中xj，k，yj，k为目标j的位置，，为第i个传感器的位置，～N(0，σ2)为测量噪声，此时测量方程为非线性形式，因此需采用EKF或UKF配合使用RBPF算法。

图6给出了雷达的角度测量值随时间的变化情况，从图6中可以看出，针对两个传感器及两个目标可测量得到4组测量值，同时在视场范围内存在一定数量的杂波测量值。

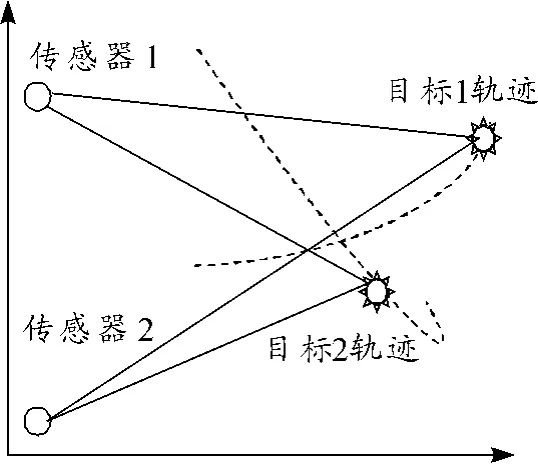
图5 双目标雷达测角示意图

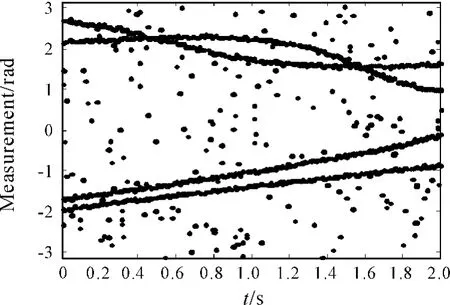
图6 雷达角度测量值随时间的变化关系

从图7可见，采用原始RBPF算法得到的目标轨迹估值与真实值在飞行中段明显存在一定的偏差，从粒子散布的变化情况看，在这一阶段采用的粒子无法覆盖真实轨迹造成其估值与真值逐渐偏离，且在偏离时刻明显两个目标的测量值较为接近。可以通过增加粒子数目来解决此问题，但这会大大增加算法的计算量。经进一步分析可知由于实时调用RBPF算法计算的有效粒子数目neff未必能够反映目标机动情况下的运动轨迹，当前权值较小的状态未必不是后期的真实状态，重采样导致粒子集中在当前权值较大的粒子附近，对其他位置的粒子进行舍弃。为此使用上文中介绍的改进重采样算法，综合考虑各种不同域内权重的粒子来确定后续的粒子分布，使得粒子的多样性增加，仿真结果如图8所示。

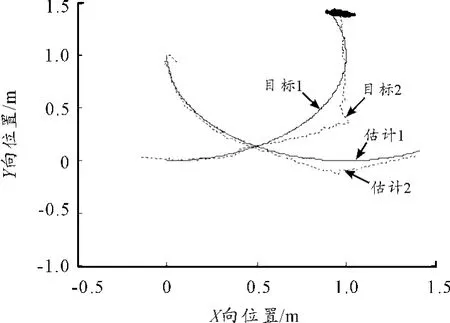
图7 采用原始RBPF算法滤波得到的目标估计轨迹

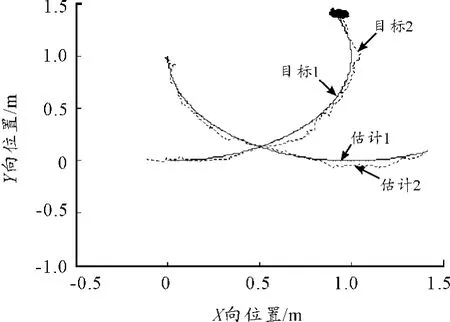
图8 采用改进重采样算法RBPF得到的目标估计轨迹

下面比较两种滤波方法的估值与真值的差的均方根的变化情况，如图9所示。

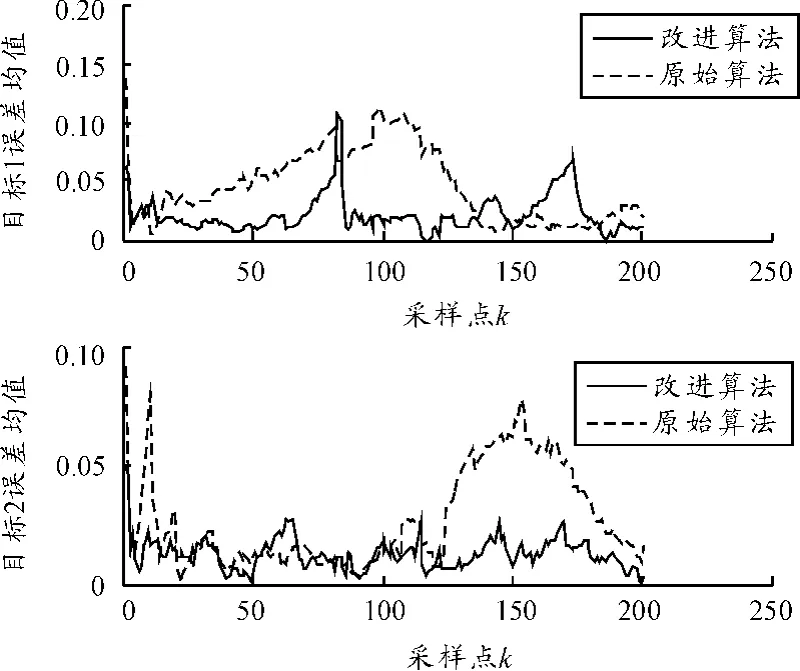
图9 两种算法滤波估值与真值的误差均值比较

4 结论

为解决仅有角度测量信息的雷达双目标跟踪问题，在此对Rao－Blackwellized粒子滤波算法进行改进，为增加粒子的多样性，解决滤波局部存在的不收敛问题，将重采样算法进行改进，增加小权重粒子的比例，同时为获得更高的滤波精度，采用交互多模型的方法对粒子的估值进行预测与更新，通过算法更改及数字仿真验证可以看出，更改后滤波算法的收敛性更好且跟踪精度更高。

［1］Kalman R E.A new Approach to Linear Filtering and Prediction Problems［J］.Transactions of the ASME，Journal of Basic Engineering，1960，82(1):35－45.

［2］Sunahara Y.An Approximate Method of State Estimation for Nonlinear Dynamical Systems［J］.Joint Automatic Control Conference，University of Colorado，1970，92(2):385－393.

［3］Julier S，Uhlman J.A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators［J］.IEEE Transactions on Automatic Control，2000，45 (3):477－482.

［4］Oliver C，Simon JG，Eric M.An overview of existingmethods and recent advances in sequential Monte Carlo［J］.Proceedings of the IEEE，2007，95(5):899－924.

［5］Gordon N，Salmond D.Novel approach to non－linear and non Gaussian Bayesian state estimation［J］.Proceedings of Institute Electric Engineering，1993，140(2):107－113.

［6］Sarkka S，Vehtari A，Lampinen J.Rao－Blackwellized Particle Filter for Multiple Target Tracking［J］.Information Fusion，2007，8(1):2－15.

(责任编辑周江川)

Target Track Based on Im proved Rao-Blackwellized Particle Filter Algorithm

ZHANGWan－li1，HE Jin－gang1，ZHAO Hong－mei2
(1.China Airborne Missile Academy，Luoyang 471009，China; 2.Luoyang Institute of Electro－Optical Equipment，AVIC，Luoyang 471009，China)

In radar signal processing field，moving target tracking is always the focus.And it involves the nonlinear filter problem which is the difficult point.In this paper，we focused on the radar target tracking problem based on the Rao－Blackwellized particle filter algorithm.To improve the convergence and the precision of the filter algorithm，resample algorithm in the RBPF algorithm is improved，which is validated by numerical simulation.The simulation result shows that RBPF algorithm is improved in every aspect.

particle filter;RBPF algorithm;radar target tracking;resample

:A

1006－0707(2014)07－0082－05

format:ZHANGWan－li，HE Jin－gang，ZHAO Hong－mei.Target Track Based on Improved Rao－Blackwellized Particle Filter Algorithm［J］.Journal of Sichuan Ordnance，2014(7):82－86.

本文引用格式:张万里，何金刚，赵红梅.改进的Rao－Blackwellized粒子滤波算法在目标跟踪中的应用［J］.四川兵工学报，2014(7):82－86.

10.11809/scbgxb2014.07.024

2014－01－27

张万里(1983—)，男，工程师，主要从事导弹制导与控制、雷达信号处理研究。

TP277