基于LabVIEW的宽频时变信号阈值去噪系统设计

张俊涛, 曹梦娜, 张 涛

(陕西科技大学 电气与信息工程学院, 陕西 西安 710021)

0 引言

信号在采集和传输过程中，由于外界环境的干扰，难免会有噪声夹杂在里面，而噪声信号是影响目标信号检测与识别性能的一个重要因素，特别是在一些高精度数据的分析中，即使是微弱的噪声都会对分析结果产生巨大的影响，所以在信号分析过程中，首先要对信号进行去噪处理.

信号去噪的方法主要有傅里叶分析去噪法和小波去噪法.傅里叶分析去噪法[1]对信号整个时间域上的信号进行频谱分析，一旦信号从时域变换到频域就会失去所有的时域特征，不能提供信号在某个局部时间段上的频率信息，对于非平稳信号的分析有一定的局限性.而小波变换恰好克服了这种局限性[2]，在时频域都具有良好的局部特性，可以聚焦到信号的任何细节，是一种窗口面积恒定、时频域形状都可变的时频局部化分析方法，具有多分辨率[3]的特点，对于时变信号进行去噪处理，既能很好地去除噪声，又不损坏信号突变的部分.

本文在对小波变换去噪方法原理研究基础之上，以宽频时变含噪信号为研究对象，采用基于LabVIEW的虚拟去噪系统对其进行多种阈值去噪，并对去噪效果进行对比分析.

1 小波变换

小波变换[4]能提供目标信号各个频率子段的频率信息，是一种强有力的时频分析工具.信号通过小波变换能够得到原始信号和噪声信号的频谱，进而为选择去噪方法提供了理论依据.

小波变换主要是利用线性变换、多分辨率分析、局部细化、可灵活选择小波基的特点，使得小波变换在信号去噪方面具有很好的效果.对瞬态非平稳信号或宽频带信号[5]，经过小波变换，设定阈值门限，调整小波系数，就可以达到小波去噪的目的.

在实际应用中还要根据实际情况选择合适的小波基函数进行去噪以获得最佳的效果.图1为常用小波基函数.

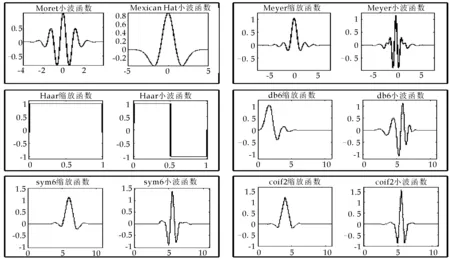
图1 常用小波基函数

2 宽频时变信号的阈值法去噪

宽频时变信号是针对具有特定频段和幅值平稳的信号定义的，它具有多个频段，是一种幅值和频率随时间变化的非平稳随机信号.

随着对信号去噪和小波算法的研究，小波去噪方法大致可以分为三大类:

(1)基于小波变换的分解与重构[6]，即根据信号和噪声在小波变换的各个尺度上的不同传播特性，对含噪信号进行分解与重构，进而恢复原始信号；

(2)对含噪信号作小波变换之后，计算相邻尺度间小波系数的相关性，根据相关性的大小决定小波系数的类型，从而进行取舍，然后直接重构目标信号；

(3)阈值法，即对小波系数设置阈值，在众多小波系数中，把绝对值较小的系数置为零，阈值法的关键在于阈值的选择.

2.1 阈值法去噪

由于阈值法[7]具有能得到原始信号的近似最优估计、计算速度快以及具有广泛的适应性等优点，因而成为小波去噪方法中应用最广泛的一种.

常用的阈值计算方法有两种[8]：硬阈值和软阈值.设y是原始小波系数，T是阈值，T(y)是阈值化后的小波系数.

(1)硬阈值(Hard Thresholding)

当小波系数的绝对值小于给定的阈值时，令其等于0，而大于等于阈值时，保持其不变.硬阈值小波系数计算方法如式(1)所示.

(1)

(2)软阈值[9](Soft Thresholding)

当小波系数的绝对值小于给定阈值时，令其等于0，大于等于阈值时，令其都减去阈值，软阈值小波系数计算方法如式(2)所示.

(2)

2.2 阈值选取准则

阈值去噪常用的阈值去噪准则有四种：

(1)Sure：基于Stein无偏/似然估计理论，是对阈值的自适应选择；

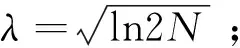
(3)混合准则Hybrid[10]：综合了无偏/似然估计和固定阈值准则，是无偏似然估计准则与固定阈值准则的折中，是最优预测变量阈值准则；

(4)极大极小值准则Minimax[11]：此项准则计算出的阈值采用的是一种最小均方差的极值，它的基本理念是将估算的最大风险尽量最小化.

2.3 阈值去噪原理

设含噪宽频时变信号为：f(k)=s(k)+n(k)，k=0，1，2,…,N-1，其中s(k)为有效信号，n(k)为噪声信号.根据小波变换的线性变换特性，对f(k)做离散小波变换，得到小波系数X(jk)=U(jk)+T(jk)，其中U(jk)和T(jk)分别是有效信号s(k)和噪声信号n(k)对应的小波系数.

根据宽频时变信号的特点，在此选择阈值法进行去噪.小波阈值去噪方法的基本思想是[12]：当X(jk)小于某个临界阈值时，认为这时的X(jk)主要是由噪声引起的，予以舍弃.当X(jk)大于这个临界阈值时，认为这时的X(jk)主要是由信号引起的，那么就把这一部分的X(jk)直接保留下来(硬阈值方法)，或者按某一个固定量向零收缩(软阈值方法)，然后用新的小波系数进行小波重构，得到去噪后的信号.

2.4 去噪效果评判标准

信号去噪效果用信噪比(SNR)和均方误差(MSE)来评判[13].去噪处理后，均方误差越小，信噪比越大，则消噪效果越好.均方差与信噪比定义分别如式(3)，(4)所示.

(3)

(4)

3 基于LabVIEW的小波阈值去噪的实现

3.1 小波阈值去噪系统的实现

小波阈值去噪系统是基于PC机和LabVIEW软件来实现的，利用LabVIEW强大的数据仿真功能来模拟语音信号产生宽频时变信号，并对信号进行处理，然后将结果显示出来.

3.2 虚拟去噪系统去噪程序框图

LabVIEW采用图形化的编程方式，与文本语言编程方式相比，具有简单直观、编程效率高的优点.LabVIEW也提供了很多针对信号处理的高级函数，扩大了在信号处理领域的应用范围.

应用小波变换处理[14]可以有效地消除各种噪声干扰，增强原始信号.利用LabVIEW提供的小波工具箱函数，应用简单的信号处理知识和编程技能，就可以通过LabVIEW搭建一个虚拟去噪系统对信号进行阈值去噪.基于LabVIEW搭建的阈值去噪程序框图如图2所示.

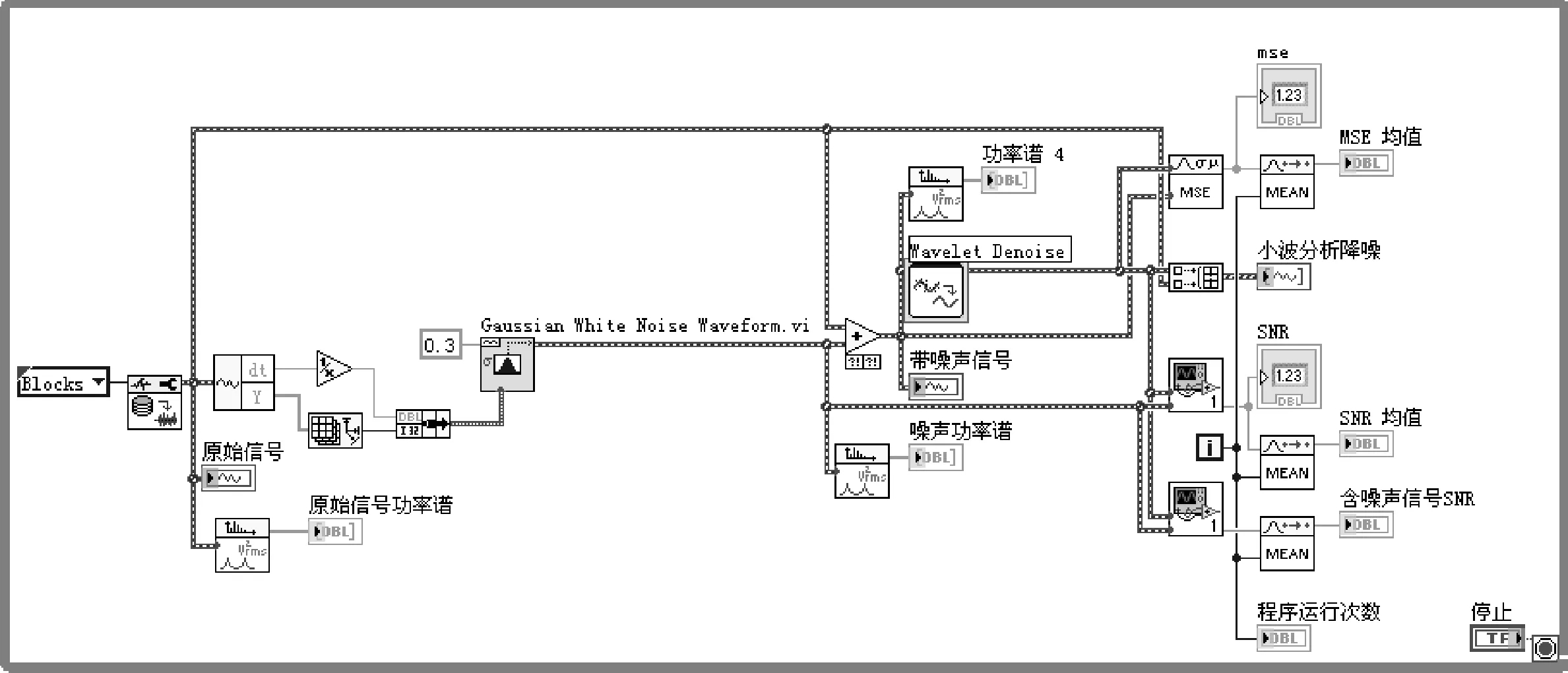
图2 LabVIEW阈值去噪程序框图

系统的实现主要分为三个部分：产生含有高斯噪声的宽频时变信号,对含噪信号进行小波阈值去噪,分析去噪后信号的信噪比和方差.图3是系统实现流程图.

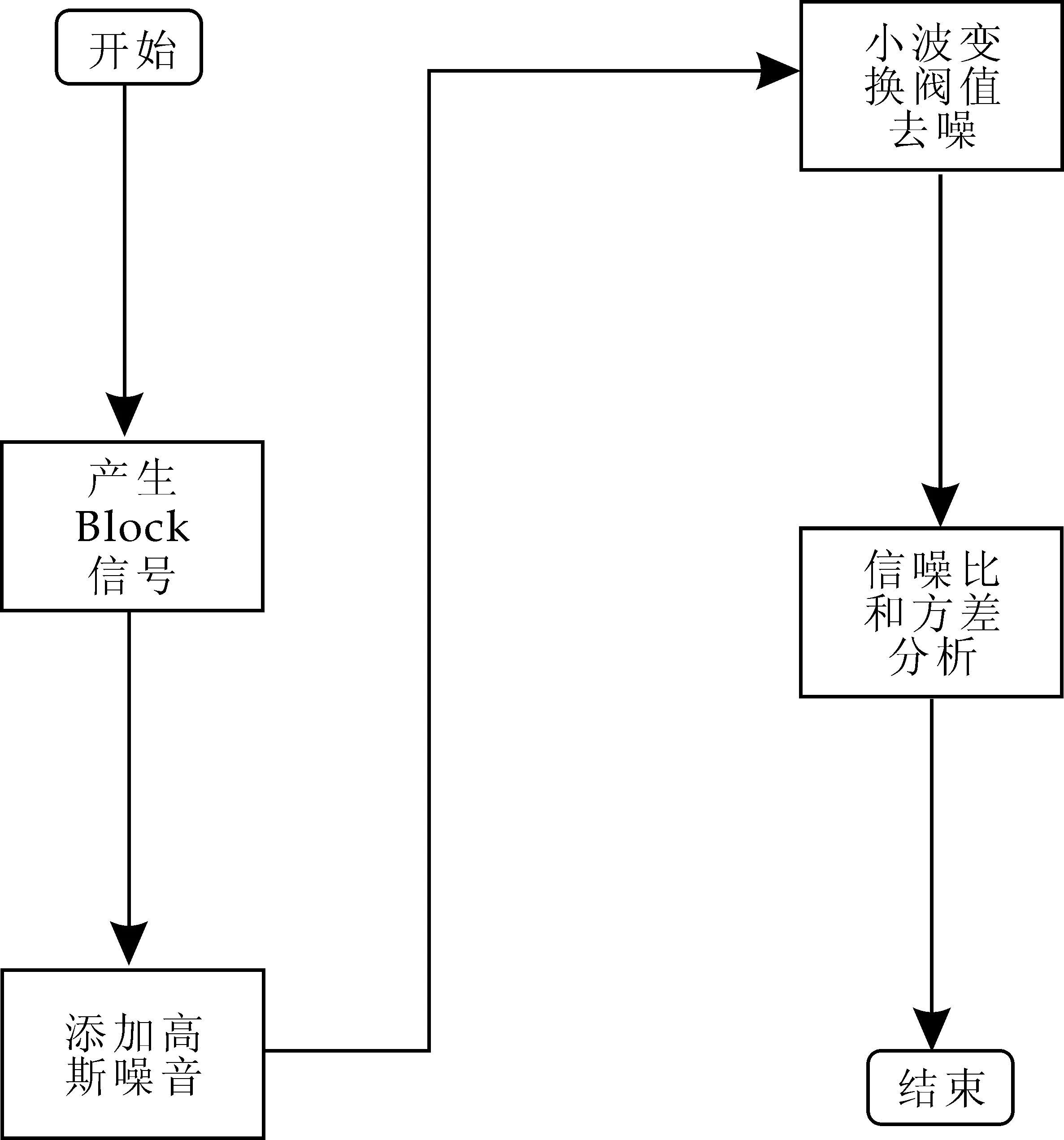
图3 系统实现流程图

3.3 去噪结果分析及对比

3.3.1 信号谱分析

用LabVIEW提供的声音信号Blocks来模拟宽频时变信号.

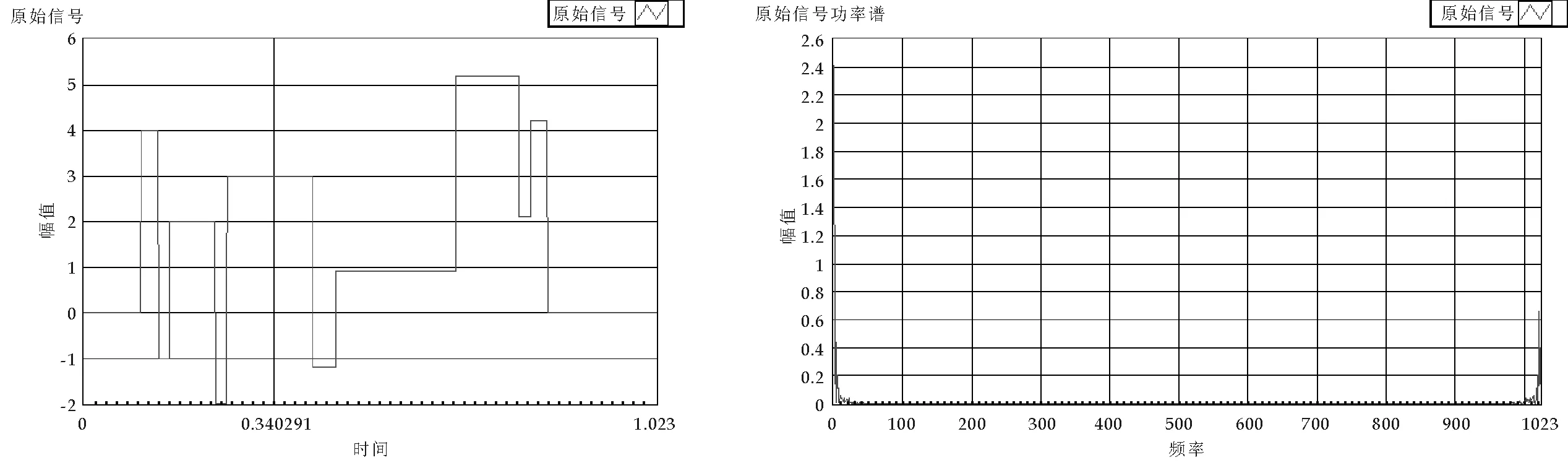
(a)原始信号 (b)原始信号功率谱

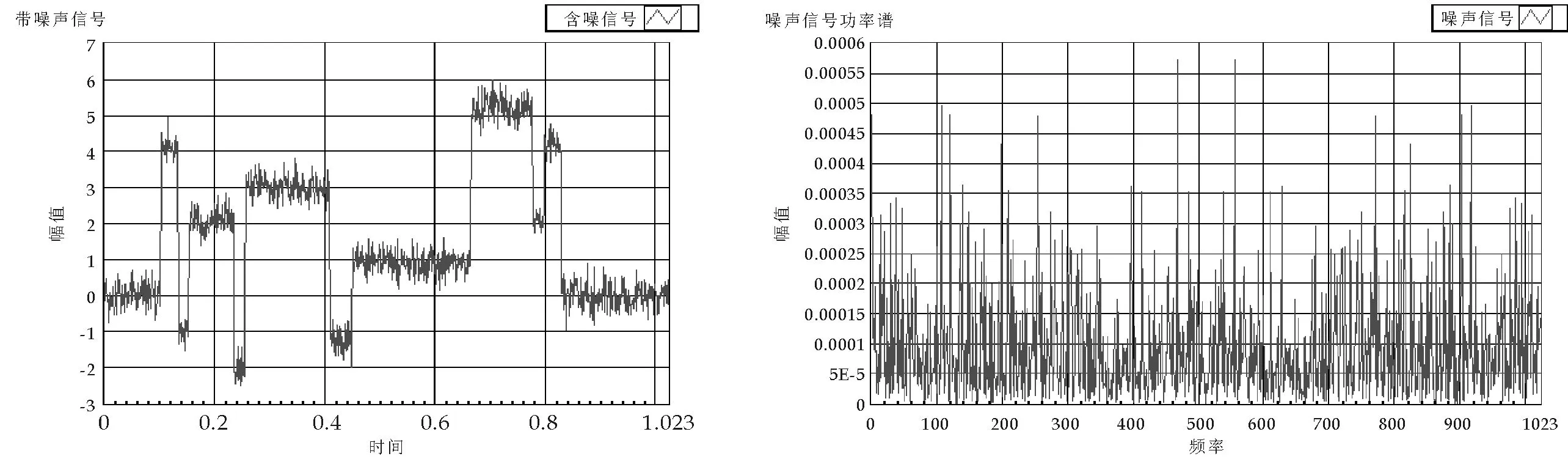
(c)含噪声信号 (d)含噪信号功率谱图4 原始信号与含噪声信号

图4(a)为原始信号；图4(b)是对原始信号进行功率谱分析，表明这种信号的低频分量和高频分量同时存在；图4(c)是混合了高斯白噪声后的信号；图4(d)是对混合了高斯白噪声后的混合信号进行功率谱分析，表明高斯白噪声同时具有高频和低频分量，但是噪声能量都比较低.

3.3.2 软硬阈值去噪结果对比分析

小波基函数[15]选取Haar函数，因为Haar波形和要被处理的原始信号的波形最类似，而和噪声波形有很大的区别；分解层数为6层，重构原理为单层重构.分别用软阈值去噪和硬阈值去噪处理，根据信噪比和方差值来评判去噪效果.

分析软、硬阈值各种准则去噪数据结果，选取了几组去噪效果比较好的数据，对比分析结果如表1所示.

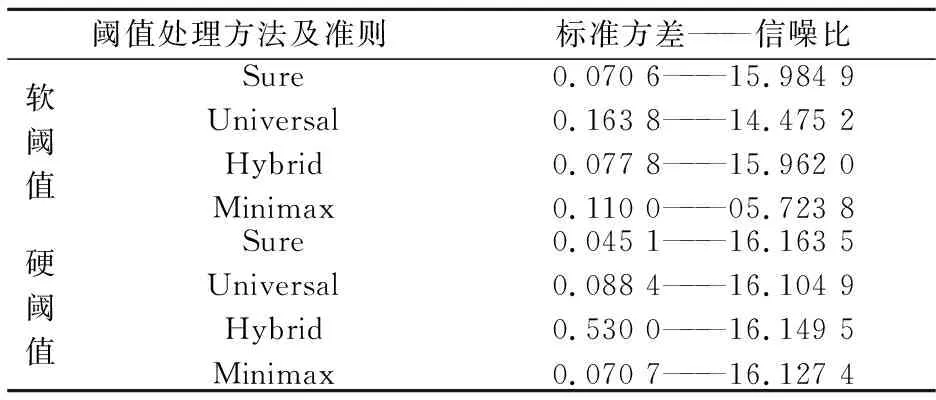
表1 标准方差和信噪比对比

综合去噪效果的评判标准即均方差和信噪比，从表1数据对比可以得出，软阈值去噪中Sure准则处理后均方差最小、信噪比最高、效果最好；硬阈值去噪中Sure准则处理后均方差最小、信噪比最高、处理效果也是最好的.

图5、图6是软、硬阈值去噪结果图.

(1)软阈值四种准则去噪波形图

(a)软Sure (b)软Hybrid

(c)软Universal (d)软Minimax图5 软阈值处理去噪后的信号结果

(2)硬阈值四种准则去噪波形图

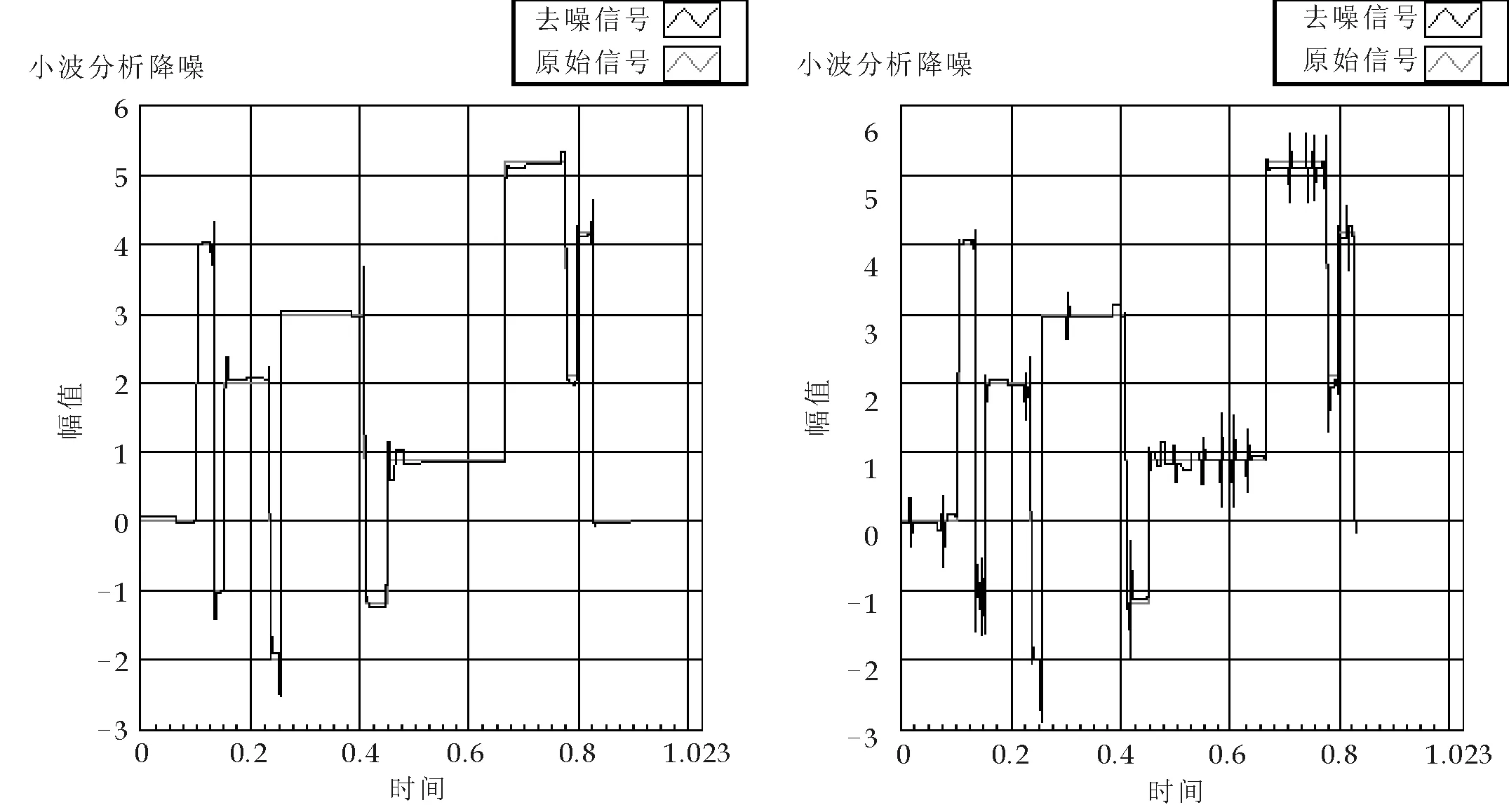
(c)硬Universal (d)硬Minimax图6 硬阈值处理去噪后的信号结果

根据表1的分析结果，分别取软阈值中的最优解Sure准则和硬阈值去噪中的最优解Sure准则，结合信号去噪后的结果如图5、图6所示，对比分析结果如表2所示.

表2 软硬阈值最优解对比图

分析表2可以看出，硬阈值比软阈值处理后的结果要粗糙一些，阈值的选择对去噪效果影响至关重要，实际情况中应根据具体情况选择合适的阈值方法、小波基函数和准则进行去噪.

4 结束语

随着小波变换的发展，基于小波去噪的方法越来越多，其优良的去噪性能也越来越多地引起人们的关注和重视.本文主要论述了小波变化中的阈值去噪准则和阈值去噪原理，搭建了一个基于LabVIEW平台的完整的虚拟去噪系统，用不同的阈值去噪算法对噪声信号进行处理并分析处理结果，取得了较好的去噪效果.

LabVIEW可以很方便地与各种数据采集设备和硬件进行交互，实现包含硬件和软件的完整系统的设计.LabVIEW图形化的编程方式具有高效直观的特点，将小波去噪在虚拟仪器中的功能丰富

和完善，为工业过程检测提供更多的方便.

[1] 毛艳辉.小波去噪在语音识别预处理中的应用[D].上海：上海交通大学,2010.

[2] 李 巍.LabVIEW实现的小波变换及其在滤波中的应用[J].国外电子测量技术,2010,29(3):11-14.

[3] 郝张红，刘先勇，袁长迎.小波去噪及其在LabVIEW中的实现[J].现在电子技术，2008，31(7)：166-167,170.

[4] 张 宁.基于小波变换的瑞利波信号去噪探析[J].电子测试，2013(10)：100-102.

[5] 王新楼.小波去噪方法分析与Matlab仿真[J].工业控制计算机，2008，21(6)：55-56.

[6] 侯 宁.基于小波分析的信号去噪方法[J].化学工程与装备，2009(8)：137-138.

[7] 张 飞.一种基于小波变换的语音信号去噪净化方法[J].电子测量技术,2009,32(6):68-71.

[8] 陈 娟,杨奇科,周晶杰.基于LabVIEW的小波变换在信号滤波中的应用[J].技术与市场,2013,20(5):51-52,54.

[9] 苑津莎,张冬雪,李 中.基于改进阈值法的小波去噪算法研究[J].华北电力大学学报(自然科学版),2010,37(5):92-97.

[10] 于 萍.用小波技术实现非平稳信号的处理[D].青岛：中国石油大学(华东)，2012.

[11] 张 燕，周西峰，郭前钢.基于LabVIEW的超声信号小波阈值去噪方法[J].计算机技术与发展，2012,22(3)：125-127.

[12] 张荣祥,李正强,郑世杰.基于遗传算法的双阈值小波去噪方法研究[J].传感器与微系统，2007，26(6)：20-22,25.

[13] 史荣珍,王怀登,袁 杰.不同小波基函数下的语音去噪研究[J].现代电子技术,2014,37(3):49-51.

[14] 姚 瑶.基于小波变换的语音信号去噪研究[J].信息通信,2013(2):13-14.

[15] 胡 瑞.基于小波变换的语音信号消噪处理设计[J].电子世界,2014(4):114-115.