非稳态注汽条件下井筒热损失计算

顾 浩， 程林松， 黄世军， 魏绍蕾， 户昶昊

(1.中国石油大学(北京) 石油工程教育部重点实验室， 北京 102249； 2.中国石油辽河油田 勘探开发研究院， 辽宁 盘锦 124000)

0 引言

在稠油热采注蒸汽阶段，准确计算井筒热损失不仅是评价注汽效果的关键，而且是分析热损失影响因素的基础，对提高蒸汽的热利用率具有重要指导意义.Ramey[1]于1962年首先建立了沿程温度分布和井筒传热模型，近年来在Ramey研究的基础上，国内外学者进行了大量改进和完善[2-9]，但是很少考虑到井口注汽条件(注入压力、温度、干度和质量流速等)随时间变化.而在实际注汽过程中，尤其对于蒸汽吞吐，由于注汽时间比较短，井口注入参数在短时间内一般很难稳定，而且现场经常需要根据地层的实际吸汽能力及时调整注汽速度或注入压力，因此，井口注汽条件往往不是恒定的.

另外，前人在计算热损失时只按井筒深度分段[10,11]，忽略了注汽时间也需分段.事实上，即使井口注汽条件保持不变，在注汽初期，井筒内的蒸汽和水泥环外缘温差较大，热损失速率也大.随着注汽的进行，温差逐渐降低，热损失速率变慢，如果仅用注汽结束时的热损失速率乘以总注汽时间和井筒长度来表征该段井筒总热损失大小，会使热损失的计算结果偏小.

为此，本文介绍了非稳态注汽条件的处理方法.在前人研究的基础上，对传热模型进行了修正，并提出了井筒总热损失表达式，为准确计算井筒热损失提供了参考.

1 数学模型

1.1 假设条件

(1)井口注汽条件(注入压力、温度、干度和质量流速等)随时间变化.

(2)井底使用封隔器，保证蒸汽不窜入油套环空，油套环空充以低压空气.

(3)忽略地层导热系数沿井深方向的变化，并视为常数.井身结构如图1所示.

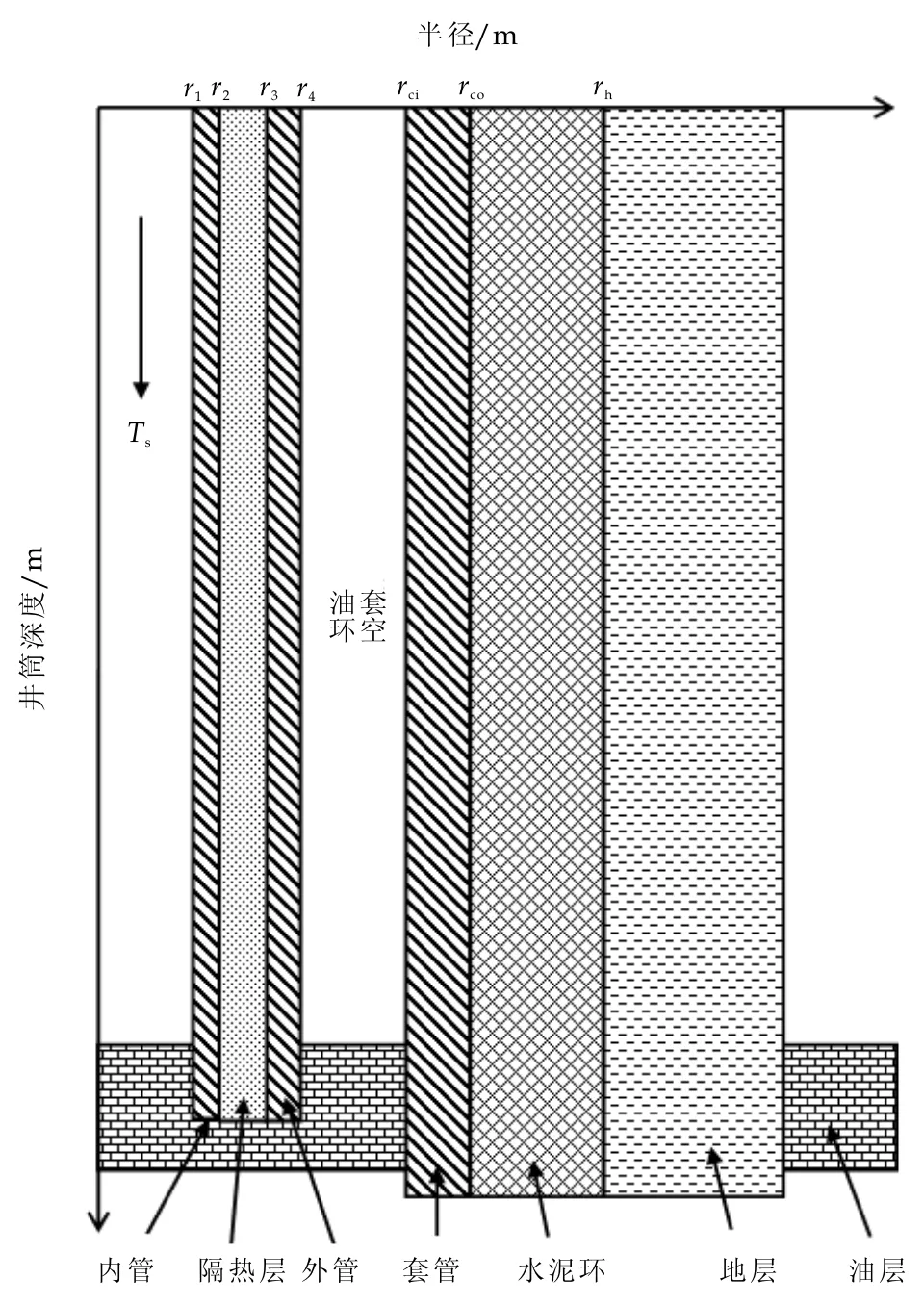
图1 井筒结构示意图

1.2 处理非稳态注汽条件

对于假设条件(1)，可以根据稳态逐次替换原理对非稳态井口注汽条件进行分段处理，其核心思想是：从整个注汽过程来看，井口注入参数(注入压力、温度、干度和质量流速等)随时间变化，但是在某一较短时间段内认为是稳定的.

具体处理方法为：将t时刻井口注入参数记作数组It=[ps,Ts,Xs,is]，从初始时刻t0=0开始依次比较，若在t1时刻，数组It1=[ps,Ts,Xs,is]中的某一个元素(ps、Ts、Xs或is)相对于t0时的注入参数It0=[ps,Ts,Xs,is]发生变化，则以t1时刻为界限，划分时间段，记作第1时间段，即在t0～t1时间段内，稳定的井口注入参数为It0，稳定注汽时间为Δt1=t1-t0；若到了t2时刻，注入参数It2=[ps,Ts,Xs,is]开始和t1时刻的注入参数It1=[ps,Ts,Xs,is]出现差异，以t2时刻为界限，再次划分时间段，记作第2时间段，即在t1～t2时间段内，稳定的井口注入参数为It1，稳定注汽时间为Δt2=t2-t1，依此类推，直到注汽结束，这里将第i时间段ti-1～ti内稳定的井口注入参数记Iti-1=[ps,Ts,Xs,is](1≤i≤n).

一般来讲，当划分的时间段数n越多时，稳态逐次替换结果就越逼近于注入参数的实际变化情况.然而，若相邻两次井口注入参数波动很小，即ti～ti+1内稳定的注入参数Iti与ti-1～ti内稳定的注入参数Iti-1在允许的误差范围内，可以对这两次注入参数取平均值，认为在ti-1～ti+1内是稳定的.

1.3 井筒传热模型

(1)油管中心到水泥环外缘的传热.当井口注汽条件发生变化时，井筒内部的传热本质上是非稳态的.为了方便计算，这里还存在一个假设：当利用稳态逐次替换法将注汽时间划分成n段后，对于第i时间段，由于井口注汽条件保持稳定，因此，在该时间段内井筒内部的传热视作稳态.根据Fourier定律，得到稳定传热公式为：

(1)

其中：

(2)

由于强迫对流换热系数h1，油套管的导热系数λtub和λcas很大，因此(2)式可以简化为：

(3)

式中，dQ为单位时间内传递的热量，W；z为井筒深度，m；r1、r2、r3、r4、rci、rco和rh分别为内管内径、内管外径、外管内径、外管外径、套管内径、套管外径和水泥环外缘半径，m；U2(i)为第i时间段内总传热系数，W/(m2·℃)；Ts(i)和Th(i)分别为第i时间段内蒸汽和水泥环外缘温度，℃；h1、hc和hr分别为强迫对流、环空内自然对流和辐射换热系数，W/(m2·℃)；λtub、λins、λcas和λcem分别为油管、隔热层、套管和水泥环的导热系数，W/(m·℃).

(2)水泥环外缘到地层的不稳定传热.其控制方程为：

(4)

初始条件和内外边界条件分别为：

Te=Tei=T0+azsinθ(t=0,r≥rh)

(5)

(6)

(7)

通过无因次转换和Laplace变换，最终得到地层温度分布为：

(8)

式中，Te为t时刻，半径r处的地层温度，℃；Tei为井深处z的初始地层温度，℃；T0是地表温度，℃；α是地层平均热扩散系数，m2/s；a为地温梯度，℃/m；θ是井筒与水平方向的倾斜角，°；λe为地层导热系数，W/(m·℃)；无因次时间τD=αt/rh2；无因次半径rD=r/rh；u为拉式空间变量；Y0和Y1分别为第二类零阶和第二类一阶贝塞尔函数；J0和J1分别为第一类零阶和第一类一阶贝塞尔函数.

令rD=1，得到水泥环外缘温度为：

(9)

其中，

根据(9)式，得到：

(10)

其中，f(t)=2I/π，为无因次地层导热时间函数，这里采用Hansan[12]表达式：

(11)

(12)

从式(9)可以看出：水泥环外缘温度Th是时间的函数，即使井口注汽条件保持不变，Th仍随注汽时间的延长逐渐增加，如图2中的曲线所示.

传统算法忽略了分时间段计算Th，导致用式(10)计算热损失速率并不准确.况且，对于非稳态注汽条件，尤其当井口注入参数发生剧烈变化时，由于水泥环外缘温度Th既与当前注入参数有关，也受之前注入参数的影响.因此，需要分时间段计算Th，并且在计算热损失速率前要对式(10)进行修正.

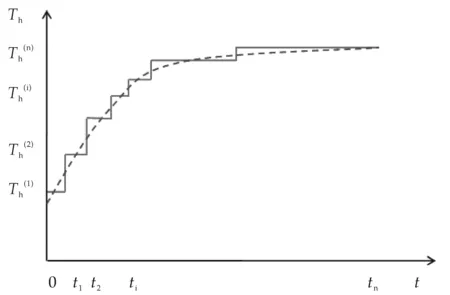
图2 水泥环外缘温度变化曲线

利用前面的稳态逐次替换法将井口注入参数分段处理后，因为第i时间段ti-1～ti内井口注入参数是不变的，所以水泥环外缘温度Th(i)在该时间段内也近似视作常数.显然，当划分的段数n越多时，图2中的折线就越逼近于实际水泥环外缘温度曲线.这里需要注意的是，如果第i时间段稳定注汽时间Δti=ti-ti-1较长，可以将该时间段再次均匀细分成N段，N越大，细分后的稳定注汽时间越短，水泥环外缘温度变化就越小.此时，就可以根据叠加原理对式(10)进行改写，得到第i时间段单位深度上的热损失速率为：

(13)

联立式(1)和式(13)，得到第i时间段内水泥环外缘温度为：

(14)

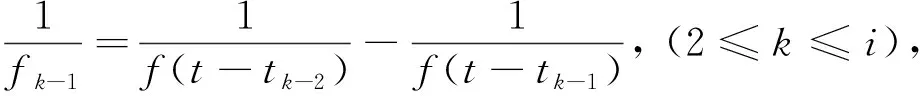
1.4 总热损失表达式

由于对井筒深度和注汽时间都进行了分段，因此，式(1)中的dQ/dz其实是井筒中某一微元段dz在第i时间段ti-1～ti内的热损失，若整个井筒被分成m段，则第j+1 (0≤j≤m-1) 深度段在整个注汽过程中总热损失大小为：

(15)

另外，还可以得出整个井筒在注汽过程中总热损失大小为：

(16)

式中，(Qt)j+1和Qt分别为第j+1深度段和整个井筒在注汽过程中的总热损失，J；(dQ/dz)j+1,i为第j+1深度段在第i时间段内单位深度上的热损失速率，W/m；Δti为第i时间段的时长，s；Δz为深度步长，m.

2 模型求解

蒸汽压力、温度和干度模型采用文献[13]中的方法，将改进后的井筒传热模型与蒸汽压力模型和干度模型联立求解，求解流程如图3所示.

图3 求解流程图

3 实例应用

3.1 基本参数

井深850 m，内管内径0.031 0 m，内管外径0.036 5 m，外管内径0.050 9 m，外管外径0.057 2 m，套管内径0.080 7 m，套管外径0.088 9 m，水泥环外缘半径0.123 6 m，隔热层导热系数0.06 5W/(m ·℃)，水泥环导热系数0.933 W/(m ·℃)，地层导热系数1.73 W/(m ·℃)，地层平均热扩散系数1.03×10-7m2/s，地表温度20 ℃，地温梯度0.031 ℃/m.某低渗稠油区块某吞吐井每天注入参数如表1所示.

表1 井口注入参数随时间变化

3.2 结果分析

图4为计算得到的井筒沿程压力与实测值对比，可以看出两者比较接近，说明所建立的模型是可靠的.

图5为590～600 m深度段内单位深度上的热损失速率与注汽时间之间的关系.可以看出：即使在相同深度段内，热损失速率也不是定值.因此，某深度段在注汽过程中的总热损失大小应该将各时间段内的热损失叠加.通过计算得到590～600 m深度段在注汽过程中总热损失大小为1.42×106kJ，整个井筒在注汽过程中总热损失大小为1.23×108kJ.

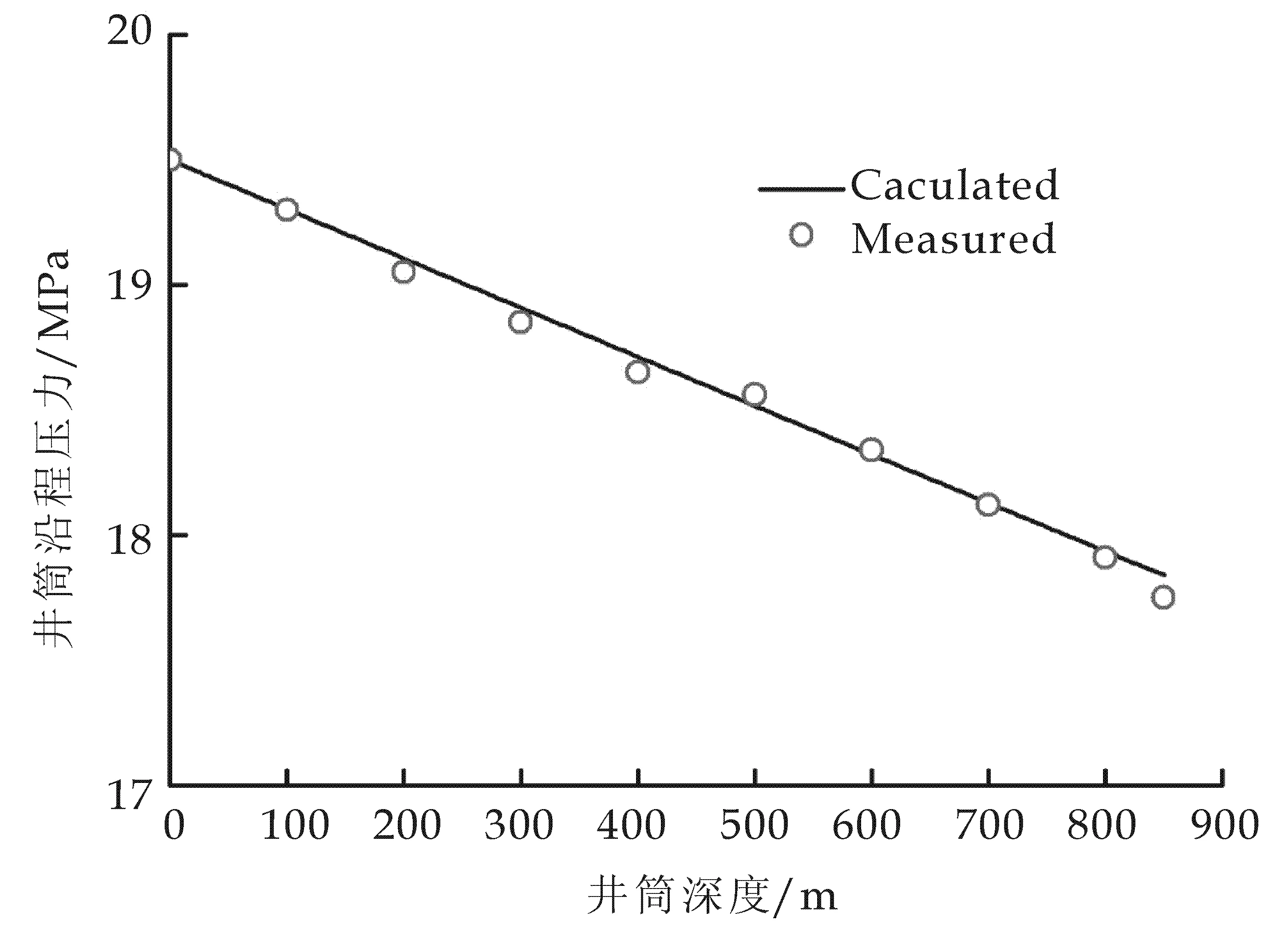
图4 井筒沿程压力计算值与实测值对比

图5 热损失速率与注汽时间之间的关系

4 结束语

在实际注汽过程中，尤其对于蒸汽吞吐，井口注入参数往往会随时间变化，以往的井筒传热模型很少考虑到这一点，并且在算法上只按井筒深度分段，忽略了注汽时间也需分段，导致井筒热损失的计算结果并不准确.

为了进一步完善热损失计算模型，利用稳态逐次替换法将非稳态井口注汽条件分段处理，根据叠加原理对传热模型进行了修正，并按时间和深度分段求解整个模型，最后提出了井筒总热损失表达式，为准确计算井筒热损失提供了参考.

[1] Ramey H J.Wellbore heat transmission[J].Journal of Petroleum Technology，1962，14(4)：427-435.

[2] 王弥康.注蒸汽井井筒热传递的定量计算[J].石油大学学报(自然科学版)，1994，18(4)：77-82.

[3] 陈月明.注蒸汽热力采油[M].东营：石油大学出版社，1996：64-83.

[4] 倪学峰，程林松，李春兰，等.注蒸汽井井筒内参数计算新模型[J].计算物理，2005，22(3)：251-255.

[5] 周体尧，程林松.注过热蒸汽井筒沿程参数计算模型[J].西南石油大学学报(自然科学版)，2009，31(1)：153-155.

[6] 东晓虎，刘慧卿，闫凤林，等.异常温压复合地层注热流体井井筒传热计算[J].广西大学学报：自然科学版，2012，37(2)：406-411.

[7] Alves L N，Alhanatl F J S，Shoham O.A unified model for predicting flowing temperature distribution in wellbore and pipes[J].SPE Production Engineering，1992(11)：363-367.

[8] Banonar M，Azaiez J，Chen Z.Two issues in wellbore heat flow modelling along with the prediction of casing temperature in steam injection wells[J].Journal of Canadian Petroleum Technology，2011(1)：43-63.

[9] Xu A Z，Mu L X，Fan Z F，et al.New fingdings on heatloss of superheated steam transmitted along the wellbore and heating enhancement in heavy oil reservoirs[C]// SPE International Petroleum Technology Conference.Beijing，China：The Society of Petroleum Engineers，2013：1-10.

[10] 李兆敏，杨建平，林日亿.氮气辅助注蒸汽热采井筒中的流动与换热规律[J].中国石油大学学报(自然科学版)，2008，32(3)：84-88.

[11] 周体尧，程林松，何春百，等.注过热蒸汽井筒沿程参数及加热半径计算模型[J].石油勘探与开发，2010，37(1)：83-88.

[12] Hansan A R，Kabir C S.Heat transfer during two-phase flow in wellbores：PartⅠ-Formation temperature[C]//SPE Annual Technical Conference and Exhibition.Dallas，Texas：The Society of Petroleum Engineers，1991：469-478.

[13] Wen L C，Yong H H，De T L，et al.A novel analytic transient heat-conduction time function for heat transfer in steam injecion wells considering the wellbore heat capacity[J].Enerty，2011，36(1)：4 080-4 088.

[14] Beggs H D，Brill J P.A study of two-phase flow in inclined pipes[J].Journal of Petroleum Technology，1973(5)：607-617.

[15] Willhite G P.Over-all heat transfer coefficients in steam and hot water injection wells[J].Journal of Petroleum Technology，1967(5)：607-615.