基于LabVIEW的应力-能量法应用软件设计

刘 乘, 王金梅

(陕西科技大学 设计与艺术学院， 陕西 西安 710021)

0 引言

目前，保护产品在流通过程中免遭冲击、振动等机械载荷损坏的最有效的常用办法，是在包装中添加缓冲材料，对产品进行缓冲保护.缓冲设计通常建立在对环境条件的统计数据处理结果、产品脆值测定和缓冲材料特性测定等试验的基础上[1].采用自由跌落的重锤对缓冲包装材料施加冲击载荷，模拟运输过程中缓冲包装材料受到的冲击作用，即动态压缩试验，可获得缓冲包装材料的动态冲击缓冲曲线以及包装件的脆值，为缓冲包装材料设计提供重要的设计依据[2].

传统缓冲材料的缓冲曲线通过跌落试验机来测定，试验需要五组式样，每组五块，每块样品至少跌落五次.则要获取一条最大加速度-曲线至少需要125次跌落试验，耗时费力，且测定曲线范围有限[3-5].

针对传统方法求取缓冲材料最大加速度-静应力曲线的缺陷，美国Hewlett-Packard公司研发中心经理Matthew Datum博士等人提出了测定缓冲材料缓冲曲线的快速预测法：应力-能量法[6].

1 应力-能量法求取缓冲材料缓冲曲线的原理[7]

应力-能量法是根据能量守恒定律，并以缓冲材料受到冲击过程中没有能量损失为前提，认为重锤在跌落过程中产生的势能转化为动能全部被缓冲材料吸收.在大量试验的基础上，推出经验公式：

E=σsth/t

(1)

式中：E动能量，σst静应力，h跌落高度，t缓冲材料厚度.

假设动应力与动能量存在以自然对数的底做参数的指数函数关系：

σm=aebe

(2)

式中：σm动能量，a、b材料常数，由缓冲材料的类型和密度确定，拟合后可以得到.

由

σm=Gmσst

(3)

得

(4)

式中Gm为缓冲材料最大加速度值，再结合实验过程中记录的σst值，从而可以得出缓冲材料的Gm-σst曲线.

2 试验

选择密度为0.014 3 g/cm3厚度为48 mm的EPS作为试验对象，跌落高度为60 mm,参考ASTM D1596依据GB/T 8167-2008进行.

由

σst=W/A

(5)

式中W为重锤重量，A为试样接受冲击的表面积.为了精确，选择五个W、A、h、t相同的缓冲材料作为一组，且每组单个式样进行五次冲击实验，求取最大加速度平均值，得到一组对应的Gm、E值.划分能量范围，选取不同的能量值，重复上述过程，测出对应的Gm、E[8].

本试验测得五组实验数据，如表1所示：

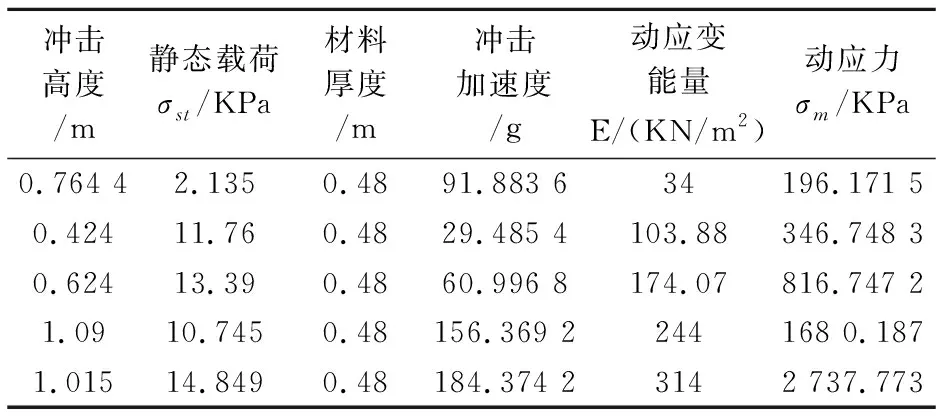
表1 动能量和动应力计算值

3 软件

LabVIEW是一种用图标代替文本行创建应用程序的图形化编程语言，采用数据流编程方式，用图标表示函数，用连线表示数据流向[9].

根据应力-能量法求取缓冲曲线的原理，显然,若根据以往试验已知某种材料函数关系中的a、b值，则可直接代入公式求得任意高度、任意厚度的缓冲曲线族.如果a、b未知，但通过试验测得一组应力-能量值，则同样可求得a、b，获得曲线族.因此确定如图1所示的程序流程图.

图1 程序流程图

3.1 设置基本参数

程序要求设置基本参数，包括材料名称、材料密度、材料厚度、跌落高度以及温湿度.由于参数的数据类型不同，采用簇来实现试验参数的保存.

3.2 数据处理与曲线拟合

3.2.1a、b未知，实验获取动能量-动应力值

实际中，通常需要根据试验所得的数据，近似地求取变量之间的函数关系，最常用的数学方法为插值和曲线拟合.插值是在离散数据之间补充一些数据，使这组离散数据能够符合某个连续函数.利用它可以通过函数在有限点处的取值情况估算该函数在别处的值，即通过有限的数据得出完整的数学描述.拟合则是利用有限个数据点，求近似函数，不要求过已知数据点，只要求在某种意义下它在这些点上的总偏差最小[10,11].

根据试验所得到的五组动应力动能量数据，创建簇元素动能量和簇元素动应力，创建簇数组常量，常量值为程序设置的基本参数值，然后进行插值.根据经验将插值方法设定为样条插值，初始值为最小能量值34，插值步长为0.01，结束值为最大能量值314.然后按最小二乘法进行指数拟合求出最大加速度-静应力曲线(如图2所示).

图示结果表明拟合效果非常不错，曲线形状非常理想.曲线最低点坐标为s=0.007 5 Mpa，Gm=41.06 g.国标法测得的曲线最低点坐标为：s=0.008 125 Mpa，G=33 g.同时得到a=167.267，b=0.009 16.

图2 a、b未知时求得的最大 加速度-静应力曲线

3.2.2a、b已知时，由软体获取能量-动应力值

由动应力-动能量法经验公式，当a、b值已知时，代入其他基本参数，则可直接获取最大加速度-静应力曲线.程序利用公式节点，方便明了[12].创建公式节点Gm=aebE/s，将a、b、h、t以及静应力s作为输入，Gm作为输出.

现已知密度为0.005 3 g/cm3的发泡聚乙烯a=218.7，b=0.009 1，要求厚度为50 mm的该材料在跌落高度为60 cm时的最大加速度静应力曲线.根据上述操作方法进行拟合[13]，结果如图3所示.

4 程序设计

程序选用条件结构，选择器端子为“是否输入A、B值”，从而选择执行相应的程序，如图4、图5所示.

考虑到在要求相对精确的场合下，用户得到的应力能量值可能多于五组，因此程序创建多列列表框，应用属性节点创建项名，使用索引数组函数分别索引列表框奇数和偶数行作为动能量和动应力输入数据，利用十进制字符串至数值转换控件将索引字符串数组转换为数值数组，将数值表示法转换为双精度.

选用多列列表框可使前面板整洁，清晰，并可任意调整行列数，灵活方便.

图6为程序整体框架图.

图4 输入a、b程序框图

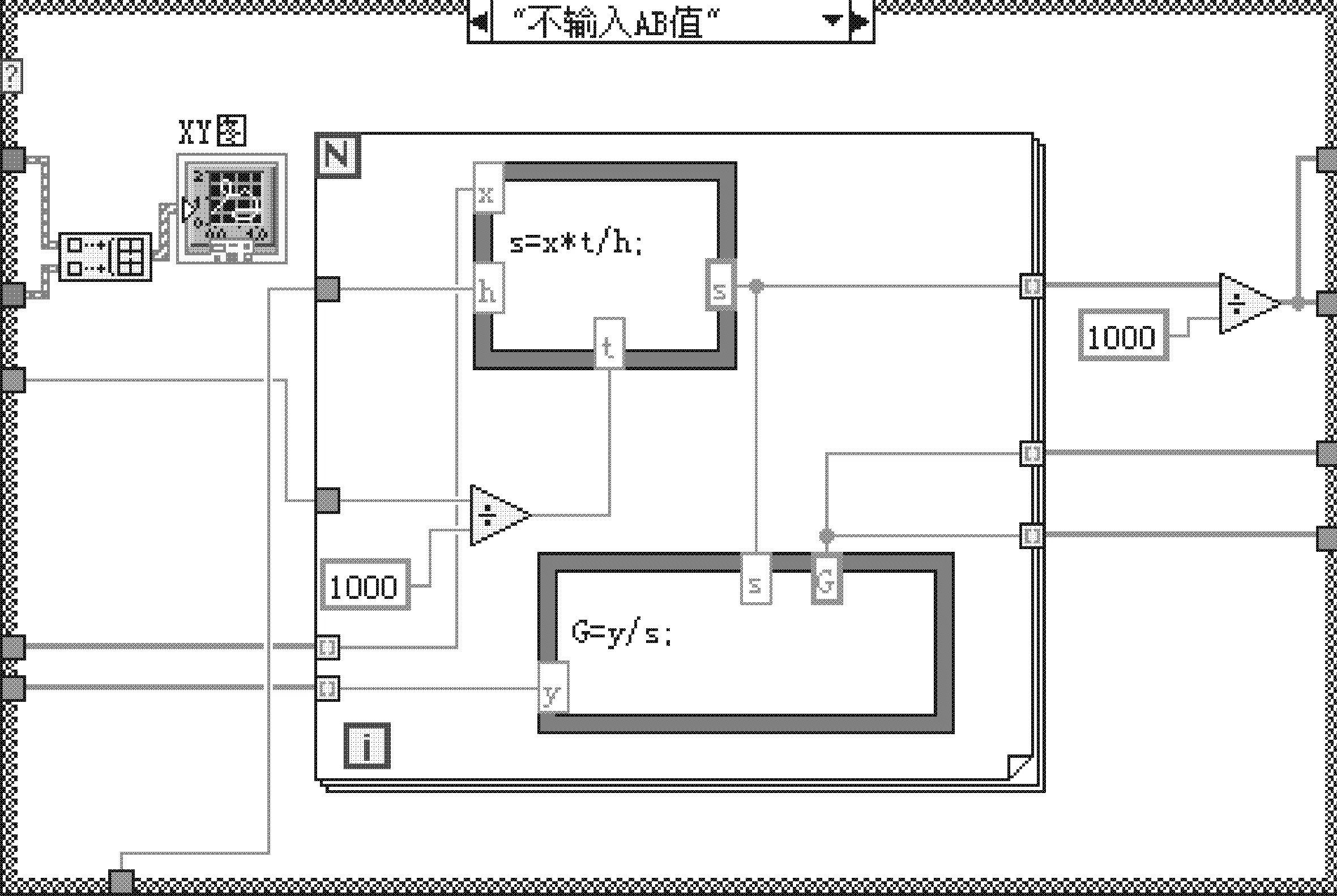
图5 不输入a、b程序框图

5 软件操作实例

假设用户已知密度为0.015 g/cm3的EPS的A、B值分别为208、0.008.要得到该材料在跌落高度为60 cm时的缓冲曲线族(厚度分别为40 mm、45 mm、50 mm、55 mm和60 mm).假设操作时温度为32 ℃摄氏度，湿度为60%.在各输入框内输入相应参数后，运行程序得到5条曲线.

图7中对各曲线代表的材料厚度做出标识，厚度从上到下依次为40 mm、45 mm、50 mm，55 mm、60 mm.

图6 程序整体框图

图7 最大加速度-静应力曲线族

6 总结

本论文以密度为0.014 3 g/cm3厚度为48 mm的发泡聚苯乙烯为例，试验证明根据应力能量法测得的数据进行缓冲包装设计更为保守.分析认为误差主要来源于：

(1)利用应力-能量法确定缓冲材料最大加速度-静应力曲线的前提是：缓冲材料在受到冲击过程中没有能量损失.但实际上重锤的重力势能并未全部被缓冲材料吸收，造成主要误差.

(2)国内包装用发泡聚苯乙烯的加工方式存在多样化，产品的密度不稳定，产品的成分不明确，造成同批产品会存在厚度规格不同导致密度的差异.所以，在使用动应力-动应变能量曲线方法中还存在部分推算加速度与实际加速度差值较大的现象.

(3)由于获取实际加速度的试验环境和设备调试不宜控制，过高的冲击高度、过轻和过重的静态载荷都会造成实际加速度偏离推测加速度.

但是不可否认，应力能量法确实拓宽了测试包装材料缓冲特性的思路，在一些精度要求不高的缓冲设计中，可作为设计人员首选参考方法[14,15].

因此，利用LabVIEW设计出基于应力能量法测试缓冲曲线软件将使动态压缩试验变得更加简便、快捷.对于一种材料，如果知道a、b值，则通过软件可以直接求得同种材料任意高度、任意厚度的缓冲曲线族；或者试验获得某种材料的若干动能量、动应力值，在界面直接输入，同样可以求得a、b值，以及缓冲曲线族.

该软件大大减少了动态压缩试验时间、人力、物力，操作简单，结果明了.

[1] 卢 杰，焦丽娟，周廷美.基于LabVIEW的缓冲材料动态压缩测试系统的设计 [J].武汉理工大学学报,2010,32(4),534-537,546.

[2] 彭国勋.物流运输包装设计[M].北京：印刷工业出版社，2006.

[3] 山静民.材料缓冲性能测试的GB法和能量法[EB/OL].http://www.testimpact.com/new_page_6.htm, 2011-05-26．

[4] 山静民．包装测试技术[M]．北京：印刷工业出版社，1999:115-116.

[5] GB/T 8167-2008, 包装用缓冲材料动态压缩试验方法[S].

[6] 路冰琳,孙 诚，韩雪山．运用数学拟合方法绘制动态冲击缓冲曲线的研究[J]．包装工程，2010，31(15):4-6,24.

[7] Matthew D.A simplified process for determining cushion curves:the stressenergy method[D].Michigan:Michigan State University,1999.

[8] 张波涛.应力-能量法在测定泡沫塑料缓冲曲线中的应用[J].包装工程，2008,29(1):59-65.

[9] 陈锡辉，张银鸿．LabVIEW8.20程序设计从入门到精通[M].北京：清华大学出版社，2007.

[10] 欧阳明松，徐连民.基于MATLAB的试验数据拟合[J].南昌工程学院学报,2010,29(4):24-28.

[11] 王 玲.基于MATLAB的数据曲线拟合[J].天津职业院校联合学报,2009,11(5):63-64.

[12] Robert H.Bishop.LabVIEW8实用教程[M].北京：电子工业出版社,2010.

[13] 张爱平.基于LabVIEW设计曲线拟合仪[J].华北航天工业学院学报,2004,14(3):5-7.

[14] 刘 乘，刘 晶.应力-能量法在求取包装材料最大加速度-静应力曲线方面的应用分析[J].包装工程,2011,32(1):74-75.

[15] 张华良，刘 乘.包装材料缓冲特性曲线研究及其在缓冲设计中的应用[J].西北轻工业学院学报，1990，8(3)：45-48.