对流层延迟改正模型的敏感性分析

董春来，李传奇，蒋廷臣

(淮海工学院，江苏连云港 222005)

对流层延迟改正模型的敏感性分析

董春来，李传奇，蒋廷臣

(淮海工学院，江苏连云港 222005)

简述对流层延迟改正模型，编程开发了有利于实时计算的对流层延迟修正值的软件，并基于灵敏性理念，分别针对温度、大气压及高度角变化，绘图分析霍普菲尔德、萨斯塔莫宁和勃兰克等3种改正模型的修正效果，取得了合理选用模型的有益结论。

对流层延迟；改正模型；软件；敏感性；分析研究

一、引 言

对流层普指高度为40 km以下的大气底层，其大气密度较大，大气状态复杂。对流层与地面接触并从地面得到辐射热能，其温度随高度的上升而降低，GNSS信号通过对流层时，传播路径发生折射弯曲，其折射与地面气候、大气压力、温度、湿度及信号高度角等变化密切相关，严重地影响了GNSS测量精度。常用的对流层延迟改正模型主要有霍普菲尔德(Hopfield)、萨斯塔莫宁(Saastamoinen)和勃兰克(Black)等3种，本文将对其修正效果、适用性等特点进行比较、分析与研究。

二、常用对流层延迟改正模型

1.霍普菲尔德模型

Hopfield依据气态方程PV＝RT，参考水汽压e和气压P随着高度h的增加而减小的规律，考虑变化率与重力加速度g和大气密度ρ的关系，总结分析得出模型如下

式中，温度以绝对温度的度为单位；气压P与水汽压e都以mbar为单位；高度角E以度为单位；ΔS、ΔSd、ΔSw都以m为单位。

2.萨斯塔莫宁模型

Saastamoinen建构模型时，将对流层细分为两层积分，一层是地表到高度约12 km的对流层，气体温度随高程变化的递减率设为6.5°C/km；另一层是从对流层顶至70 km左右的平流层顶。其萨斯塔莫宁模型表示为

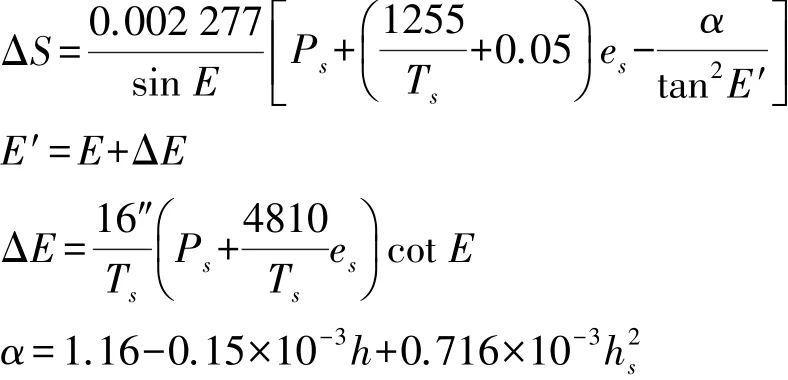
3.勃兰克模型

1978年，Black在霍普菲尔德模型的基础上加入路径弯曲之后，给出了勃兰克模型

三、对流层改正编程计算软件

为了分析对比上述几种对流层改正模型修正情况，快速选定模型并计算改正数值，笔者通过设计、编程、调试与运行，开发完成了几种对流层改正模型修正效果的自动计算与分析软件，其主界面如图1所示。

图1 对流层延迟改正计算主界面

四、改正模型灵敏性对比分析

无论以地表气象参数为基准量，还是以地区性气象模式为参考量，都涉及大量观测资料，带有经验性问题。为了比较改正模型差异，分析对流层折射的影响，本文针对不同模型，考查了气象参数影响的灵敏度变化，力求寻找反映对流层折射规律，较强适应区域性的对流层改正模型，并运用Matlab编程实现对比曲线分析，其中横坐标为考查变化量，纵坐标为不同模型延迟改正值。

1.温度改变灵敏性分析

保持高度角、气压值及高度等不变，改变温度时，各模型改正值变化情况如图2所示。

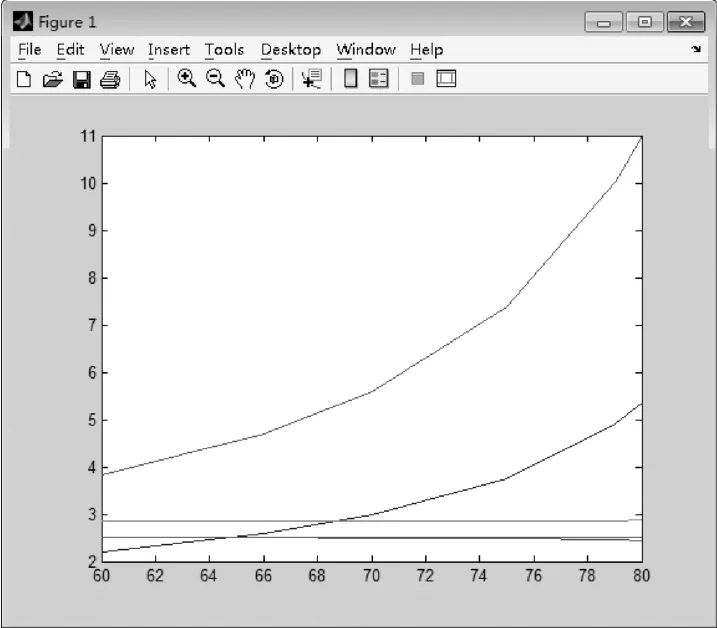
图2 改正模型受温度的影响

由图2可知，改变温度时，不同的对流层改正模型都会有不同的改正值。改正后霍普菲尔德改正模型随着温度的增大其改正值增加得最快，而且增加的幅度最大，说明该模型对温度的感知最灵敏，温度是影响其改正精度的最大因素，同时，温度也是霍普菲尔德模型的重要影响因素。而温度对改进的萨斯塔莫宁和勃兰克模型改正影响不是很大，曲线几乎为一条直线。但是温度对于萨斯塔莫宁模型则没有影响。

2.高度角变化灵敏性分析

保持温度、气压值及高度等不变，改变高度角时，各模型改正值变化情况如图3所示。

图3 改正模型受天顶距的影响

由图3可知，不同的高度角会产生不同的对流层延迟，而且不同的模型所受到的高度角影响的程度也是不同的。对于改进的萨斯塔莫宁模型来说，天顶距的变化不产生影响，其变化曲线是一条直线；对于萨斯塔莫宁模型和勃兰克模型来说，其受天顶距变化的影响程度较小，其变化曲线接近于直线。但是，对于霍普菲尔德模型和改正的霍普菲尔德模型来说，其天顶距直接影响着改正精度，在相同的温度和大气压下，霍普菲尔德模型的改正值会随着天顶距的增大而减小，改正的霍普菲尔德模型则与霍普菲尔德模型相反，会随着天顶距的增大而增大。

3.气压变化灵敏性分析

保持高度角、温度及高度等不变，改变气压值时，各模型改正值变化情况如图4所示。

图4 改正模型受大气压的影响

由图4可知，在温度和天顶距相同的情况下，改正值的增大随着大气压的增加幅度比较小，大气压对勃兰克模型改正没有影响，对其他模型的影响很微弱，其改正值的曲线也近似为直线，也近似平行，可以理解为影响程度大致相同。

五、结 论

1)对流层延迟修正模型虽然在形式上有所不同，但在精度要求不高时，采用相同的气象参数，求得天顶方向的对流层延迟较差相差不大，一般情况仅为几毫米。当高度角E＝15°时，互差则有几厘米。

2)编程实现的对流层延迟改正计算软件，能快捷解算延迟改正的效果值，直观反映各个模型在相同气象参数条件下的差异，更方便研究对流层对GNSS高精度测量的影响。

3)若温度变化，所有改正模型计算出来的改正值都会随着温度的增加而增大；若高度角变化，萨斯塔莫宁模型和勃兰克模型影响较小，霍普菲尔德模型的变化较大；而大气压的改变对所有模型的改正值影响不明显。

[1] 徐绍铨，张华海，杨志强，等.GPS测量原理及应用[M].武汉：武汉大学出版社，2008：103-105.

[2] 王新龙，李亚峰.GPS定位中4种对流层延迟修正模型适应性分析[J].电光与控制，2008(11)：5-9.

[3] 徐杰，孟黎，任超，等.对流层延迟改正中投影函数的研究[J].大地测量与地球动力学，2008(5)：120-124.

[4] 周金国，崔书珍，彭军还.GPS对流层延迟改正模型及其InSAR应用研究[J].测绘通报，2009(11)：1-3.

[5] 李凯锋，欧阳永忠，任来平，等.GPS精密单点定位中对流层延迟处理方法研究[J].测绘科学，2009，34(4)：93-95.

[6] 杨玲，李博峰，楼立志.不同对流层模型对GPS定位结果的影响[J].测绘通报，2009(4)：9-12.

[7] 徐杰，孟黎，任超，等.对流层延迟改正中投影函数的研究[J].大地测量与地球动力学，2008，28(5)：120-124.

[8] 李昭，邱卫宁，邱蕾，等.几种对流层延迟改正模型的分析与比较[J].测绘通报，2009(7)：16-18.

[9] 曲伟菁，朱文耀，宋淑丽，等.三种对流层延迟改正模型精度评估[J].天文学报，2008，49(1)：113-122.

[10] 高星伟，陈锐志，李夕银.中性大气对非差伪距定位的影响及其模型改正分析[J].测绘学报，2007，36 (2)：135-138.

[11] 徐彦田，程鹏飞，蔡艳辉，等.估计对流层延迟的单频RTK卡尔曼滤波算法[J].测绘通报，2012(8)：15-17.

Sensitivity Analysis of Tropospheric Delay Correction Model

DONG Chunlai，LI Chuanqi，JIANG Tingchen

P228

B

0494-0911(2014)09-0070-03

2013-07-06

国家自然科学基金(41004003)；江苏省海洋资源开发研究院开放基金(JSIMR1303)

董春来(1963—)，男，安徽安庆人，教授，主要从事大地测量及数据处理方面的教学与研究工作。

董春来，李传奇，蒋廷臣.对流层延迟改正模型的敏感性分析[J].测绘通报，2014(9)：70-72.

10.13474/j.cnki.11-2246.2014.0297