马尔可夫更新过程在武器装备可靠性方面的应用

余 超，陈夫凯，周 浩

(河海大学 理学院，南京 210098)

马尔可夫更新过程在武器装备可靠性方面的应用

余 超，陈夫凯，周 浩

(河海大学 理学院，南京 210098)

区别于单一武器装备寿命分布分析，考虑综合性情况下的非马尔可夫型冷储备可修系统，应用马尔可夫更新过程理论建立可靠性分析模型，并计算出武器装备的2种可用度。

马尔可夫更新过程;冷储备可修系统;可用度;梯形法

对部队来说，优良的武器装备是衡量队伍战斗力的重要指标，而装备的可靠性则是衡量武器优良的重要指标，因而分析武器装备的可靠性是重要的研究课题。一般对于武器装备来说，常会对其寿命进行可靠度分析。如文献［1］对寿命服从威布尔分布的武器装备进行了可靠性分析，并提出了相应的维修方案。文献［2］介绍了寿命分布为威布尔分布的设备相关理论，用参数估计方法分析了发动机叶片的故障率及可靠度。文献［3］介绍了可靠性理论中分布函数的各可靠性指标。但是仅考虑寿命分布却远远不够，如设备是否可修、修理工修理时间导致的部件暂时停止工作等问题均使得部件系统变得复杂。而对于满足非马尔可夫型冷储备可修系统的武器装备，可以根据马尔可夫更新过程理论对其进行分析建模。文献［4］详细说明了马尔可夫更新方程的推导过程并将其应用于实例。文献［5］阐述了可用度基本含义及其计算模型。对于满足两同型部件冷储备模型的侦察系统［6］及有延误的单部件可修系统的装甲装备［7］，已有文献研究了其可靠性。而冷储备系统在国内已经拥有非常成熟的理论系统，如曹晋华、程侃［8］详细说明了非马尔可夫型两部件冷储备系统的3种可靠性指标。文献［9］具体分析了具有2个不同部件和2个修理工的冷储备系统的主要可靠性指标。文献［10］讨论了有延迟的2不同型部件的可靠性指标。这些均对部队武器装备的可靠性分析提供了理论依据。对于部件系统的可靠性指标，主要分析其瞬时可用度和稳态可用度，但是对于满足马氏更新方程的可用度，利用拉普拉斯及其反变换往往很难计算。陶建峰等［11］用复合梯形法计算出了2种可用性指标。本文在更新理论、马氏更新过程理论、拉普拉斯及拉普拉斯－斯蒂尔切斯变换和概率分布理论［12］的基础上，首先说明了可靠性理论中的单一考虑部件寿命的可靠性研究，然后分析了具有1个修理工和2种不同型部件的冷储备系统，并用梯形法计算出武器装备的瞬时可用度和稳态可用度。

1 可靠性理论中的2种分布函数分析

1)指数函数

对非负随机变量X有密度函数f(x)=ue－ux，u＞0，x≥0，称X服从参数为u的指数分布。它是可靠性工程常用的分布，其特点是失效率u是常数。这意味着可靠性是时间的函数，但不是元件寿命的函数。有可靠度函数R(t)=e－ut，失效率函数为u，平均寿命为1/u。

2)威布尔分布函数

对于上两种函数，虽然可以经过统计分析得出元件的相关可靠性指标，但对于部件出现故障、修理工加入系统、部件工作暂停，以及修理工因为假期及个人原因导致修理延迟等问题，运算将会变得十分复杂，不仅是考虑部件寿命的问题。但对于非马氏冷储备系统却可以应用马氏更新过程理论来解决。

2 马尔可夫更新过程

2.1 马氏更新过程定义

设随机变量 { X(t)，t≥0 }是状态空间E=Z+的随机过程，设0=t0＜t1＜t2＜…＜tn＜…是过程的状态转移时刻，则Xn=X( tn+0)是过程在时刻tn发生的第n次转移后所处状态。若对任意整数n≥0，任意i0，…，in－1，in，j∈E和任意t≥0，有

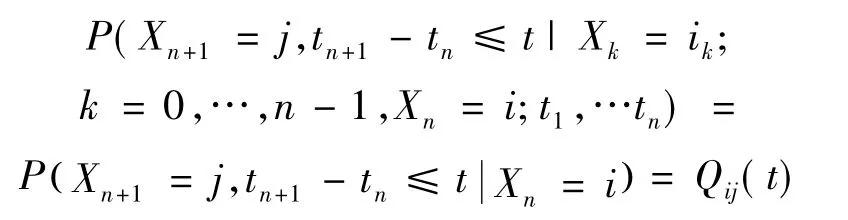
则称随机过程 {(Xn，tn)，n≥0 }为马尔可夫更新过程。转移概率族 {Qij(t)，i，j∈ E}，称作空间E上的半马尔可夫核。设 X(t)=Xn，tn≤t≤tn+1，则{ X(t)，t≥0 }是半马氏过程。Xn称作半马氏过程{ X(t)，t≥0 }的嵌入马氏链。

2.2 再生点

再生点是这样的时刻:在已知此时该过程所处的状态的条件下，过程将来发展的概率与过去的历史无关。

在马尔可夫过程中，每个状态的逗留时间服从指数分布［13－15］。由于指数的无记忆性，任意时刻t都是过程的再生点，具有马氏性。但在半马尔可夫过程中，逗留时间分布为一般分布，故所有时刻并非都是过程的再生点，而只在状态转移时刻是再生点。

3 装备的模型分析

3.1 模型假设

假设1 系统由2个不同型部件和2个修理工组成。

假设2 部件的工作寿命Xi服从威布尔分布W( αi，λi;x)=Wi(x)，i=1，2，故障后修理时间Yi服从参数为μi的指数分布Fi( ui;y)，i=1，2。

假设3 2个部件的工作寿命、修理时间以及修理延迟时间都相互独立，且在工作之初是全新的，部件既不出现故障也不会劣化。

假设4 装换开关是可靠的，状态转移是瞬时的，部件修复如新。

此时所建立的模型即两部件冷储备系统模型。

3.2 状态分析

状态0 部件1开始工作，部件2冷储备;

状态1 部件1出现故障，修理延迟开始，部件2开始工作;

状态2 部件2出现故障，开始修理，修理延迟开始，部件1开始工作;

状态3 一个部件正在工作，另一个部件修理结束;

状态4 一个部件正在修理延迟，另一个部件发生故障。

经分析知:状态0是滑过状态，状态1、2都是系统的再生点。在再生点时刻与状态{X，T}相关的函数f( i，t)=P( A)定义在E×R+上满足马尔可夫更新方程:

其中:g=P( A，T1＞t)，Q=P( I[s≤t]，i，k)，T1为首次更新时刻。

令X(t)=j表示在时刻t系统处于状态j(j= 0，1，2，3，4)，Tn表示系统第n次发生状态转移的时刻，Zn=X( Tn+0)表示第n次转移时刻系统所进入的状态。则易知 (Zn，Tn;n=0，1，2，… )是状态空间E={0，1，2，3}上的马尔可夫更新过程，{ X(t)，t≥0 }是一个半马尔可夫过程。Qij(t)，i= 0，1，2，3，4，j=1，2，3，4，记Xi，i=1，2为装备i的工作寿命，Yi，i=1，2为装备i的修理时间，则有下列结果:

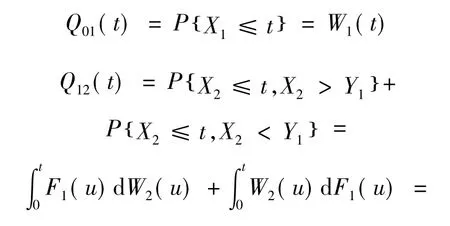
3.3 可用性分析

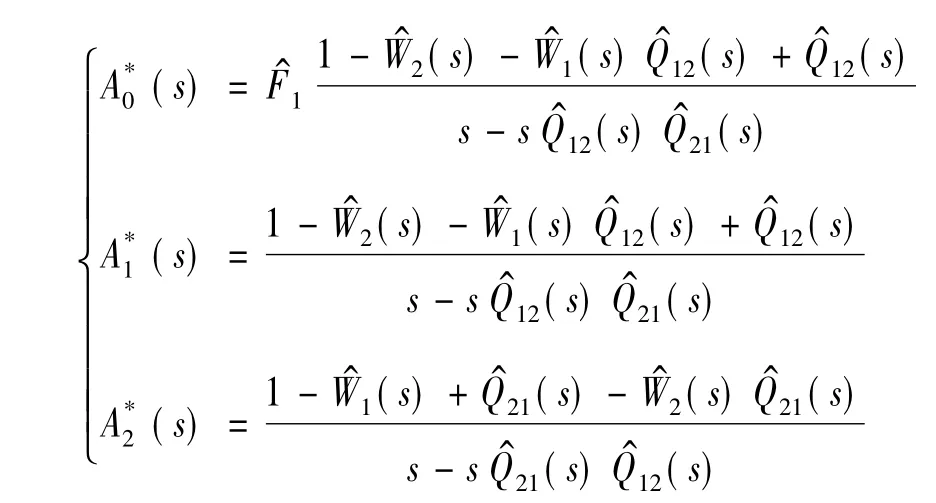
通过拉普拉斯变换及其反变换很难求出瞬时可用度A0(t)，A1(t)和A2(t)，但在所要求的精度下通过数值方法求解会使计算变得简单。本文采用梯形公式求解瞬时可用度。对A0(t)，A1(t)和A2(t)变形可得

进而可以得出系统的稳态可用度与初始状态无关。

4 模型计算

假设经过参数估计后，2个装备的寿命分布参数分别为λ1=0.01，α1=1，λ2=0.02，α2=1，修理时间参数为u1=0.5，u2=0.5，则考虑该武器装备的可用性指标。

1)稳态可用度

其A1(t)可用度在［0，100］h的曲线见图1。

图1 A1(t)可用度在［0，100］h的曲线

由图1可知:武器装备在工作时随着时间的增加，可用度逐渐减小。可见，单从稳态可靠度方面并不能反映出武器装备的瞬时可用度［16－18］，而且对于冷储备系统的工作时间通常比系统进入稳态可用度的时间短，稳态可用度很难描述系统瞬时可用度的动态变化。

5 结束语

区别于通常单一考虑部件寿命分布的可靠性研究，本文应用马尔可夫更新过程理论对武器装备进行建模分析。考虑其为具有2个不同型部件、1个修理工的冷储备可修系统，进而求出基于马尔可夫更新过程理论的武器装备的可靠性指标，以便用于实际研究与参考。但本文只考虑了两部件冷储备系统，多重装备部件的预防性维修、修理有优先权、修理工休假以及部件老化问题等尚需进一步研究。

［1］ 李阳，吴建业.基于威布尔分布的武器装备维修性分析研究［J］.舰船电子工程，2013(3):102－104.

［2］ 于晓红，张来斌.基于新的威布尔分布参数估计法的设备寿命可靠性分析［J］.机械强度，2007，29(6):932－936.

［3］ 闫纪红.可靠性与智能维护［M］.哈尔滨:哈尔滨工业大学出版社，2012.

［4］ 王丙参，魏艳华，张凡弟.马尔可夫更新过程及其应用［J］.齐齐哈尔大学学报，2011(3):86－89.

［5］ 徐廷学，杜峻名.导弹装备使用可用度验证方法［J］.四川兵工学报，2011，32(8):1－3.

［6］ 沈吉峰，张永志.基于马尔可夫更新过程的侦察系统可靠性分析［J］.兵工自动化，2010，29(32):447－450.

［7］ 刘福胜，单志伟.基于马尔可夫更新过程的装甲装备使用可用度模型［J］.装甲兵工程学院学报，2010，4 (5):15－17.

［8］ 曹晋华，程侃.可靠性数学引论［M］.北京:科学出版社，1986.

［9］ 李才良，薄冰远.两不同部件冷储备系统的可靠性分析［J］.电子科技大学学报，2003，33(3):331－332.

［10］尚仲平，卢淑霞.具有修理延迟的两部件冷储备的可靠性分析［J］.数学的实践与认识，2011，23(12):134－139.

［11］陶建峰，刘成良，王少萍.两部件冷储备系统可用度数值解法［J］.上海交通大学学报，2006，39(9):1476－1480.

［12］邓永录.应用概率及其理论基础［M］.北京:清华大学出版社，2005.

［13］张蕊，夏乐天.灰色马尔可夫链模型在降雨预测中的应用［J］.重庆理工大学学报:自然科学版，2012(10): 103－106.

［14］刘金全，李楠，郑挺国.随机波动模型的马尔可夫链－蒙特卡洛模拟方法——在沪市收益率序列上的应用［J］.数理统计与管理，2010(6):1026－1035.

［15］徐竞.基于马尔可夫链的动态CPPI投资策略及实证分析［J］.重庆理工大学学报:自然科学版，2012(4): 128－134.

［16］陈辉强，魏鑫，高飞.装备可靠性数据处理方法［J］.四川兵工学报，2010(7):35－37.

［17］王贵宝，龙立军，邱欣.武器装备可靠性工程研究现状与最新进展［J］.直升机技术，2011(1):25－29.

［18］康锐，曾声奎，王自力.装备可靠性系统工程的应用模式［J］.中国质量，2013(4):16－18.

(责任编辑 刘 舸)

Application of Markov Renewal Process in the Credibility Aspect of Weapon Equipment

YU Chao，CHEN Fu－kai，ZHOU Hao
(Shool of Sciences，Hohai University，Nanjing 210098，China)

To make a distinction from the analysis of life span distribution about the single weapon equipment，the paper considered the non－Markov in comprehensive situation，used the Markov renewal process theory to build the reliability analysis model，and calculated the two kinds of usability.

Markov renewal process;the cold standby repairable;usability;delay time

O22

A

1674－8425(2014)07－0137－05

10.3969/j.issn.1674－8425(z).2014.07.027

2014－03－06

余超(1991—)，男，江西临川人，硕士研究生，主要从事统计与随机过程和水文预报方面的研究。

余超，陈夫凯，周浩.马尔可夫更新过程在武器装备可靠性方面的应用［J］.重庆理工大学学报:自然科学版，2014(7):137－141.

format:YU Chao，CHEN Fu－kai，ZHOU Hao.Application of Markov Renewal Process in the Credibility Aspect of Weapon Equipment［J］.Journal of Chongqing University of Technology:Natural Science，2014(7):137－141.