含风险调整适应函数的价格动态模型

马鸿燕

(新疆大学数学与系统科学学院，乌鲁木齐 830046)

含风险调整适应函数的价格动态模型

马鸿燕

(新疆大学数学与系统科学学院，乌鲁木齐 830046)

在做市商机制下建立含有风险调整适应函数的价格动态模型，考虑具有一支风险资产和一支无风险资产股票的市场，市场中考虑两类投资者(基本面分析者和图表分析者)，其中图表分析者采用最简单的交易规则。运用离散动力系统局部渐进稳定性和分支理论对其相应的确定系统进行分析。

做市商;风险调整;图表分析者;稳定性

近年来，有关异质信念资产定价引起了广泛的讨论。在真实的金融市场中，不同的投资者对未来收益的预期和对风险的态度并不完全相同。Brock和Hommes［1］提出了异质信念贴现资产定价模型，将实现的净利润作为适应函数，但并没有考虑获得此利润时所承担的风险。在随后的文献(Guanersdorfer［2］、Hommes［3］、Gaunersdorfer［4］和Gaunersdorfer and homes［5］)中使用风险调整实现利润作为适应函数，得到由它导出的需求函数与期望方差最大化导出的需求函数一致。波动聚集是金融时间序列的一种重要的特征，之前的文献都是在数值模拟中给出其说明，但没有给出理论解释。Gaunersdorfer and homes［6］同样考虑了风险调整适应函数，并给出了波动聚集的理论证明。确定市场出清价格有两种使用最广的机制，即瓦尔拉斯拍卖机制和做市商机制。前者广泛应用于经济理论，但O’Hara指出它只能用在一种市场中，即伦敦的白银市场。上述文献都是在瓦尔拉斯拍卖机制下讨论的。

1 模型

这部分建立一个异质信念标准贴现资产定价模型。有关风险调整适应函数的相关文献(例如: Guanersdorfer［2，4］、Gaunersdorfer and Homes［5－6］)中都是在瓦尔拉斯拍卖机制下考虑的。本文将在做市商机制下考虑价格的动态。

根据Brock and Hommes［1］的模型结构，考虑具有一支风险和一支无风险资产股票的两类资产市场，假定无风险资产在总收益R＞1时是完全弹性供应的。Pt为t时期风险资产的价格，{yt}为其股息过程，t时期h型投资者的财富动态表示为:

其中:zh，t为t时期h型投资者购买风险资产的股数;Rt+1=Pt+1+yt+1－RPt是每股的超额收益; Ft={Pt，Pt－1，…;yt，yt－1，…}为信息集。令Et，Vt为基于信息集Ft的条件期望和方差，Eh，t，Vh，t为h型投资者对条件期望和方差的信念。

假定投资者是近视均值最大化者，则股数需求zh，t满足

其中，a为风险厌恶系数。令nh，t为h型投资者的市场分数。假设风险资产的外部供给为0，则超额需求ze，t规定为

市场价格是通过做市商机制(参考文献［7］)调节的，即:

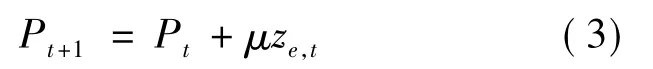
其中，μ为每时期做市商调整市场价格的速度。

对信念做以下简化假设:A1:假设未来价格和股息的形式为

类型1为基本面分析者，认为未来价格将以速率v向基本价格P*方向移动，当v接近0(1)时，基本面分析者认为价格快速(缓慢)地向基本价格移动;类型2为图表分析者，从历史价格中推出他们的信念，其中式(4)是图表分析者使用最近观察的价格变化的交易规则的一个简单例子。若g＞0则为追风者;若g＜0则为逆风者。

市场分数定义如下:首先，在演化部分由离散选择概率确定:

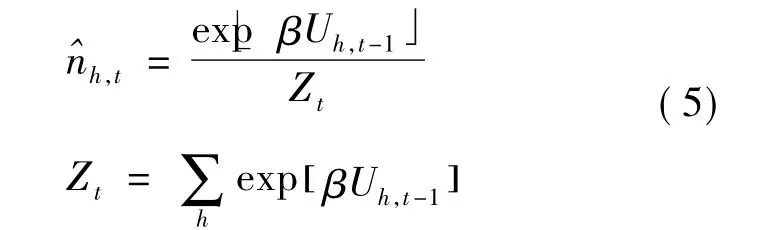
其中Uh，t为适应函数。

Brock and Hommes［1］将实现净利润作为适应函数，t时期实现的净利润定义为:πh，t=Rtzh，t－1。然而这里没有考虑到获得此利润所承担的风险，因此采用风险调整实现净利润，定义为

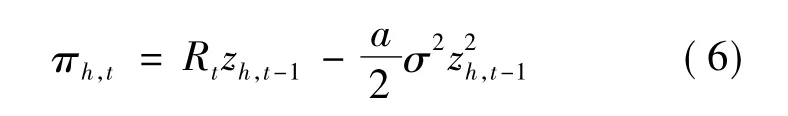
根据式(6)，风险调整实现净利润作为适应函数与财富短期期望方差最大化导出的需求函数一致。详细讨论参考文献［6］。简单的推算可得适应函数为

其中，0≤η≤1为适应函数的记忆强度。

图表分析者使其市场分数取决于偏离基本价格的模型为

根据式(8)，当市场价格偏离基本价格P*越远时，图表分析者的市场分数将减小。它是由定义市场分数取决于偏离基本价格这一事实激励的。详细讨论可参考文献［5］。

2 确定性系统的稳定性分析

这部分讨论确定系统在平衡点的存在性和平衡点附近的局部渐进稳定性［8－9］。令 xi+1，t= Pt－i－P*，得到随机模型(9)的5维确定性系统，可表示为:

定理2得证。

由定理2可得:当μ增大时，稳定区域Ω1增大，Ω2减小;当μ减小时，稳定区域Ω1减小，Ω2增大。Gaunersdorfer and Homes［7］得到的稳定区域只有1个，而本文得到2个稳定区域，对于稳定性而言更详细一些。

当参数改变时，会出现引起动态系统质的变化的分支，特别是会出现改变平衡点稳定性的分支。在这样的分支值点处，平衡点是非双曲线的，即存在一个平衡点处的雅克比矩阵所对应的特征根的绝对值为1。也就是有一个特征根的值为1，－1或一对共轭复根。考虑到当只有一个参数发生改变时出现的余一维分支，易得如下结论:

3 结束语

本文在做市商机制下，建立含有两类投资者的具有风险调整适应函数的单资产动态模型。分析了确定系统平衡点的存在性，运用差分系统渐进稳定性理论讨论了系统在平衡点处的稳定性及分支讨论，得出在做市商机制下稳定区域比在瓦尔拉斯拍卖机制下的稳定区域要详细，即它的稳定性更好。

［1］ Brock W C.Hommes.Heterogeneous beliefs and routes to chaos in a simple asset pricing model［J］.Journal of Economic Dynamics and Control，1998，22(8/9):1235－1274.

［2］ Gaunersdorfer A.Endogenous fluctuations in a simple asset pricing model with heterogeneous beliefs［J］.Journal of Economic Dynamics and Control，2000，24(5): 799－831.

［3］ Hommes C H.Financial markets as nonlinear adaptive evolutionary systems［J］.Quantitative Finance，2001，1 (1):149－167.

［4］ Gaunersdorfer A.Adaptive belief systems and the volatility of asset prices［J］.Central European Journal of Operations Research，2001，9:5－30.

［5］ Gaunersdorfer A，Hommes C.A nonlinear structural model for volatility clustering［M］.Berlin:Springer Berlin Heidelberg，2007.

［6］ Gaunersdorfer A，Hommes C H，Florian O，et al.Bifurcation routes to volatility clustering under evolutionary learning［J］.Journal of Economic Behavior and Organization，2008，67(1):27－47.

［7］ Chiarella C，He X.Heterogeneous beliefs，risk and learning in a simple asset pricing model with a market maker［J］.Macroeconomic Dynamics，2003，7(4):503－536.

［8］ 王联，王慕秋.常差分方程［M］.乌鲁木齐:新疆大学出版社，1991.

［9］ 王东华，钟晓珠，梁景翠，等.一类高阶中立型差分方程的正解存在性［J］.武汉理工大学学报，2007，28 (12):145－147.

(责任编辑 刘 舸)

Evolutionary Learning in a Simple Asset Pricing Model with a Market Maker

MA Hong－yan1，SUN Qing－gang2
(1.Institute of Mathematics and Systems Science，Xingjiang University，Urimqi 830046，China; 2.Institute of science and technology，Xingjiang University，Urimqi 830008，China)

In a market maker scenario，we develop a simple asset pricing model with two types of rational traders，fundamentalists and chartists.Chartists use the simplest trading rule.Use local asymptotic stability of discrete dynamical systems and bifurcation theory for the analysis of underling deterministic system.

market maker;risk adjustment;chartists;stability

O211.9

A

1674－8425(2014)07－0123－04

10.3969/j.issn.1674－8425(z).2014.07.024

2014－03－18

国家自然科学基金资助项目(41261087);新疆文科基地重大项目(0601920)

马鸿燕(1990—)，女，宁夏人，硕士研究生，主要从事数理金融方面的研究。

马鸿燕.含风险调整适应函数的价格动态模型［J］.重庆理工大学学报:自然科学版，2014(7):123－126.

format:MA Hong－yan，SUN Qing－gang.Evolutionary Learning in a Simple Asset Pricing Model with a Market Maker［J］.Journal of Chongqing University of Technology:Natural Science，2014(7):123－126.