一种工业过程稳态优化控制的新算法

徐恭贤，邢彦冰，吕迎皓，刘颖

(渤海大学数理学院，辽宁锦州 121013)

一种工业过程稳态优化控制的新算法

徐恭贤，邢彦冰，吕迎皓，刘颖

(渤海大学数理学院，辽宁锦州 121013)

针对一类工业过程稳态优化控制问题，基于系统优化与参数估计集成方法(ISOPE)，提出了一种可求其最优解的迭代优化算法。ISOPE方法的一个关键步骤是估计过程输出导数。为了有效地估计过程输出导数，提出了一种最小二乘方法。与已有的ISOPE方法相比，该算法不仅获得了工业过程稳态优化控制问题的最优解，而且具有计算成本低的优点。

工业过程;稳态优化控制;导数估计;最小二乘法;优化算法

虽然工业过程一般是按照一定设计运行的，但是原料成分的变化、噪声的影响、设备老化等因素都会对工业过程的正常运行形成扰动。因此，基于标称模型的优化解会偏离实际系统的最优值，严重时甚至会违反实际系统的约束条件。解决此类问题的一个有效方法是采用系统优化与参数估计集成(ISOPE)的稳态优化方法［1-9］。其基本思想是使用修正子来协调系统优化和参数估计这2个子任务，使其交替进行，直至收敛到最优解。使用方便有效的过程输出导数估计方法对ISOPE算法至关重要。实际过程输出导数的估计方法目前有［10-15］:有限差分法［10］，对于小规模工业过程、无噪声的情况是快速有效的，但是一旦环境变动或系统规模较大时，会耗时较多且误差较大。双重控制优化法［11］，能很快估算到数值，并且不需要多次改变设定点值;其局限性在于矩阵必须是非奇异的，因此对于初始值的设定要求较高;如果引入条件数约束来改进该方法，则需要求解一个非凸的非线性优化问题［9］，比较困难。Broydon算法［12］，可以避免计算偏导数，但是BR矩阵的更新过程相对复杂，每一次更新都需要测量一次当前的输出值并进行初始化。动态模型识别法［13］，是一种有效的近似估算导数的方法，特别适用于慢变过程［14-15］。

基于以上考虑，本文提出了一种可用于求解工业过程稳态优化控制问题的迭代优化算法，基于ISOPE方法框架并应用最小二乘方法估算过程输出导数。数值结果表明，本文提出的算法无论在计算时间上、还是在迭代次数上都优于传统的ISOPE方法。

1 ISOPE基本算法

考虑如下真实工业过程的稳态优化控制问题［1］:

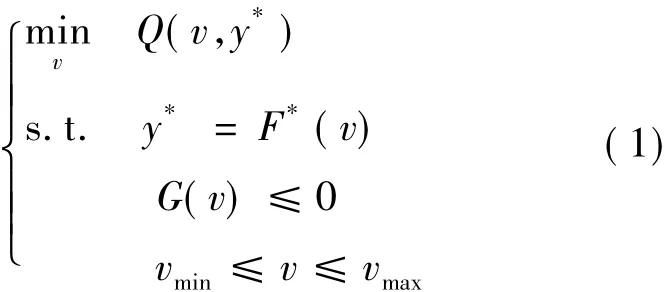
其中:v∈Rm，y*∈Rn分别是过程设定点和实际系统输出;F*表示实际过程的输入-输出描述;Q (v，y*)表示优化控制问题的目标函数;G(v)∈Rp是实际约束条件;vmin和vmax分别表示设定点的下界和上界。

一般地，可以用稳态模型y=F(v，α)近似描述真实过程y*=F*(v)，这里α∈Rl为模型参数，则优化问题式(1)可以化为:

其中，H(v，α)=Q(v，F(v，α))。

ISOPE方法的基本思想就是通过引入一个修正乘子λ来协调系统优化和参数估计这2个子问题。首先通过F(v，α)=F*(v)估计模型参数α，然后在α和λ给定的情况下(比如α=¯α，λ=¯λ)求解如下的修正模型优化问题:

2 修正的ISOPE算法

由式(4)可知:要计算修正乘子λ，就必须先估计实际过程输出导数矩阵∂F*(v )∂v。目前虽然有多种方法可以完成这一任务，但在实际应用时这些方法也存在一些局限性。比如，有限差分方法计算导数矩阵需要每次迭代都对设定点进行扰动，计算量较大;双重控制优化方法要求矩阵必须是非奇异的，如果遇到病态矩阵，就要求解非凸优化问题，计算比较困难;Broydon算法要在每次更新时对测量值进行初始化;动态模型识别法则需要找到合适的动态模型。

基于以上分析，本文提出了一种新的方法来在线估算导数矩阵。首先假设在第i次迭代时存在一些设定点vi，vi-1，…，vi-m，且Δvik=vi-vi-k线性无关，Δy*(ik)=y*(i)-y*(i-k)表示当前实际输出与第k次迭代前实际输出值的差，其中k=1，2，…，m。设

在设定点vi处实际导数矩阵［11］满足:设其最优解为ui。

Step 6若满足‖vi+1-vi‖≤ε，则停止迭代，否则更新控制设定点:vi+1=vi+t(ui-vi)。令i=i+1，返回Step 2。

3 仿真研究

为了说明本文所提算法的实用性和有效性，在Matlab环境下对如下工业过程进行了仿真实验。

实例1真实过程的稳态优化控制问题为［1］

其中:v1为塔顶回流量与塔顶馏出产物的流量比; y2为控制塔板上的乙烯浓度;为塔顶馏出产物中的乙烷浓度;为塔底馏出产物中的乙烯浓度。

仿真实验中，近似稳态模型y=F v1，v2，(α)为

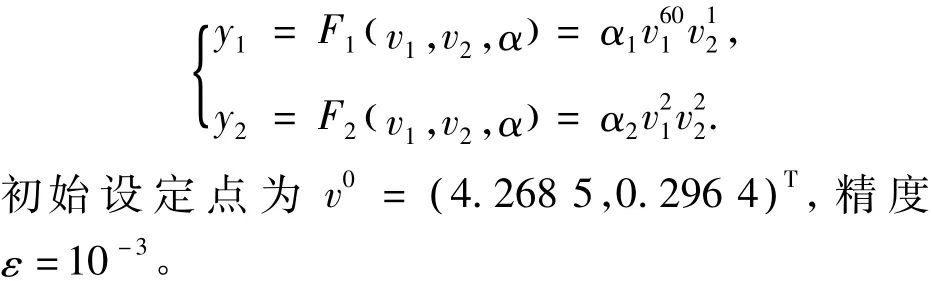
表1是无噪声情况下本文算法与已有算法的性能比较。从表1可知:本文算法与文献［9］、文献［1］方法都达到了系统的实际最优值，但是新算法的迭代次数和运行时间却远少于文献［9］和文献［1］算法。这说明本文算法在收敛速度方面要优于传统的优化算法。

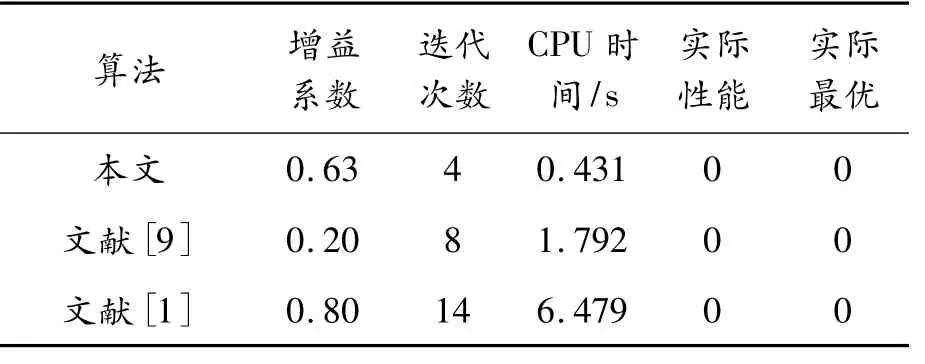
表1 无噪声条件下本文算法与已有算法的性能比较

图1、2分别给出了本文算法中噪声对实例1实际性能的影响情况。从图中可以看出:在采样过程输出时如加上滤波环节(10)，则实例1的实际性能能得到很好的改善。这说明滤波技术(10)对降低噪声对本文算法性能的敏感影响是有效的。

图1 在有噪声条件下实例1中采用本文算法的性能曲线(无滤波器)

图2 在有噪声条件下实例1中采用本文算法的性能曲线(使用滤波器)

4 结束语

本文提出了一种可用于求解工业过程稳态优化控制问题的新算法。与传统的ISOPE算法相比，该算法具有如下特点:①应用最小二乘法估计实际过程导数;②计算成本小，可应用于大规模工业过程的稳态优化控制中。

［1］Brdy M，Tatjewski P.Iterative Algorithms for Multilayer Optimizing Control［M］.London:Imperial College Press，2005.

［2］Roberts P D.An algorithm for steady state system optimisation and parameter estimation［J］.International Journal of Systems Science，1979，10(7):719-734.

［3］Roberts P D，Williams T W C.On an algorithm for combined system optimisation and parameter estimation［J］. Automatica，1981，17(1):199-209.

［4］Brdy M，Chen S，Roberts P D.An extension to the modified two-step algorithm for steady-state system optimisation and parameter estimation［J］.International Journal of Systems Science，1986，17(8):1229-1243.

［5］Roberts P D.Coping with model-reality differences in industrial process optimization-A review of integrated system optimization and parameter estimation［J］.Computers in Industry，1995，26(8):281-290.

［6］Tatjewski P.Iterative optimizing set-point control-the basic principle redesigned［J］.Proceedings of the 15th Triennial IFAC World Congress，Barcelona，Spain，2002.

［7］Gao W H，Engell S.Iterative set-point optimization of batch chromatography［J］.Computers and Chemical Engineering，2005，29(6):1401-1409.

［8］万百五，黄正良.大工业过程计算机在线稳态优化控制［J］.北京:科学出版社，1998.

［9］徐恭贤，邵诚.一种工业过程稳态优化控制算法［J］.控制与决策，2008，23(6):619-625.

［10］Mansour M，Ellis J E.Comparison of methods for estimating real process derivatives in on-line optimization［J］. Applied Mathematical Modelling，2003，27(4):275 -291.

［11］Brdys M A，Tatjewski P.An Algorithm for Steady-state Optimizing Dual Control of Uncertain Plants［J］.Proceedings of IFAC Workshop on New Trends in Design of Control Systems，Prague，1992:249-254.

［12］Roberts P D.Broyden derivative approximation in ISOPE optimising and optimal control algorithms［J］.Proceedings of the 11th IFAC Workshop on Control Applications of Optimization，St Petersburg，Russia，2000，293-298.

［13］Lin J，Roberts P D，Wan P B.New approach to stochastic optimizing control of steady-state systems using dynamic information［J］.International Journal of Control，1989，50 (6):2205-2235.

［14］Bamberger W，Isermann R.Adaptive on-line steady-state optimization of slow dynamic processes［J］.Automatica，1978，14(3):223-230.

［15］Zhang H，Roberts P D.On-line steady-state optimization of nonlinear constrained processes with slow dynamics ［J］.Transactions of the Institute of Measurement and Control，1990，12(5):251-261.

(责任编辑 何杰玲)

A New Algorithm for Steady-state Optimizing Control of Industrial Processes

XU Gong-xian，XING Yan-bing，LYU Ying-hao，LIU Ying
(College of Mathematics and Physics，Bohai University，Jinzhou 121013，China)

An iterative optimization algorithm for steady-state optimizing control of a class of industrial processes is proposed.The scheme is based on the Integrated System Optimization and Parameter Estimation(ISOPE)technique.A key step in the implementation of ISOPE method is to estimate the derivatives of process outputs.To efficiently achieve this task，a least square approach is presented in this work.Compared with the current ISOPE methods，our proposed algorithm not only obtains the optimal solution for steady-state optimizing control problem of industrial processes，but also has a low computational burden.

industrial processes;steady-state optimizing control;estimation of real derivative;least squares;optimization algorithm

TP273

A

1674-8425(2014)08-0076-05

10.3969/j.issn.1674-8425(z).2014.08.016

2014-05-08.

国家自然科学基金资助项目(11101051，11371071);辽宁省高等学校优秀人才支持计划资助项目(LJQ2013115)

徐恭贤(1976—)，男，辽宁庄河人，博士，副教授，主要从事最优化方法与应用研究。

徐恭贤，邢彦冰，吕迎皓，等.一种工业过程稳态优化控制的新算法［J］.重庆理工大学学报:自然科学版，2014(8):76-80.

format:XU Gong-xian，XING Yan-bing，LYU Ying-hao，et al.A New Algorithm for Steady-state Optimizing Control of Industrial Processes［J］.Journal of Chongqing University of Technology:Natural Science，2014(8): 76-80.