基于Matlab板的振动响应与声辐射研究

张媛媛，沈火明

(1.新疆农业大学水利与土木工程学院，乌鲁木齐 830052; 2.西南交通大学力学与工程学院，成都 610031)

基于Matlab板的振动响应与声辐射研究

张媛媛1，沈火明2

(1.新疆农业大学水利与土木工程学院，乌鲁木齐 830052; 2.西南交通大学力学与工程学院，成都 610031)

利用Matlab软件对矩形薄板结构振动进行了有限元分析，通过瑞利积分求出了板的表面声压，利用辐射模态理论研究了不同频率下结构声辐射模态形状的变化规律。结果表明:基于Matlab软件编写的程序能快速方便地得到薄板结构的固有频率，结果能较好地收敛并达到满意的精度;当激励频率小于第1阶频率时，其辐射声压随激励频率的增加而逐渐增大;辐射模态在低频时具有形状相似性，结构的各阶辐射模态在x-y平面内呈对称或反对称，且不随频率的变化而改变。

振动分析;板;Matlab软件;有限元;声辐射

随着科技的飞速发展及人民生活水平的提高，越来越多的结构要求自重更轻、外壳更薄、抗震减噪性能更好。板类结构重量轻、耗材少，是优良的基本结构构件，如太阳能板、车身结构等。所以研究板结构的振动与声辐射特性对于结构的减振降噪控制有着重要意义。文献［1］利用超参数壳单元建立了变厚度板的有限元方程，并求出谐波激励下板表面的位移响应和速度响应。文献［2 -3］通过数值和理论分析方法，分别获得了矩形板的模态辐射声功率的数值解和精确解。文献［4］利于SYSNOISE软件计算了平板在不同介质中的振动和声辐射。文献［5-6］从不同角度研究了流体作用下板类结构的振动声辐射问题，计算分析结构声辐射损耗因子和声辐射效率以及计算的预测代理模型。文献［7］基于分层理论，提出一种阵列式压电式传感器的设计方法测量复合材料层合板结构声辐射模态幅值。文献［8-10］研究了不同板类结构的振动及声辐射问题，并提出了主动控制的优化方案。本文利用有限元方法计算了四边固支板的动态响应，然后通过瑞利积分计算出板的表面声压，并利用结构表面辐射阻抗阵，研究了不同频率下结构声辐射模态形状的变化规律。

1 矩形薄板弯曲振动的有限元理论

薄板横向振动微分方程为

对四边简支矩形薄板固有频率有精确的解析解，对于其他复杂边界条件，只有通过数值方法才能求出各物理量的解析解。

板经单元离散后，可获得薄板振动的有限元方程:

式(4)中:M，C，K和F为系统质量矩阵、阻尼矩阵、刚度矩阵和载荷向量。

当C=0，F=0时，得结构的无阻尼自由振动方程为

设式(5)解的形式为X=ψejωt，解得

它的根ω2称为特征值，是结构固有频率的平方。

当激振为谐波激励时，可设F=F0eiωt，X= X0eiωt，F0为稳态载荷向量，X0为稳态位移响应，V0为稳态速度响应，ω0为激振圆频率。则结构的稳态位移响应为

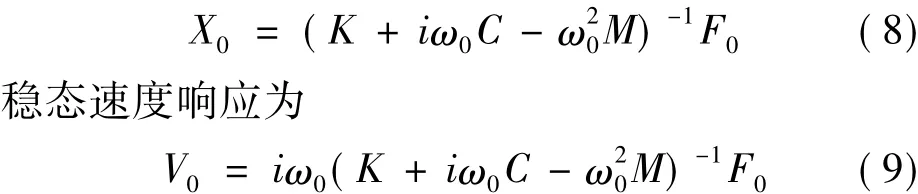
2 薄板的声辐射理论

假设板处于无限大刚性障板上。设矩形板的表面积为S，当板在在圆频率ω下振动、向上半空间辐射声波时，空间内充满均匀介质，介质密度为ρ，声速为c，振动表面上的法向振动速度为V(Z，ω)，则在该频率下板表面声压为

式(10)中:X为源点;Z为场点;r为场点和源点的距离;k=ω/c为波数;j为虚数单位。

设板的表面离散为n个四边形单元，则结构表面第j个单元中一点的速度:

式(11)中:N=［N1，N2，N3，N4］分别为单元4个结点处的形函数;Vj=［Vj1，Vj2，Vj3，Vj4］T为单元j的结点法向速度向量。

板表面经单元离散后，将式(11)代入式(10)中，可以获得单元结点处声压式(12)中:P为表面结点声压列向量;H为单元经过数值积分并经过组装后形成的系数矩阵;Vn为结点法向速度列向量。

结构表面辐射阻抗阵Δ的表达式为

3 数值仿真

设板的长度a=0.38 m，宽度b=0.3 m，板厚h=0.002 m，弹性模量E=2.1×e11，泊松比ν= 0.3，薄板的密度为ρ=7 850 kg/m3，不计结构的阻尼影响，本文仅对四边固支板进行求解，如图1所示。

3.1 板自由振动的计算

设na×nb为划分的板单元总数，现令na= 38，nb=30，得到的有限元模型如图2所示。表2为四边固支矩形薄板的前8阶固有频率。

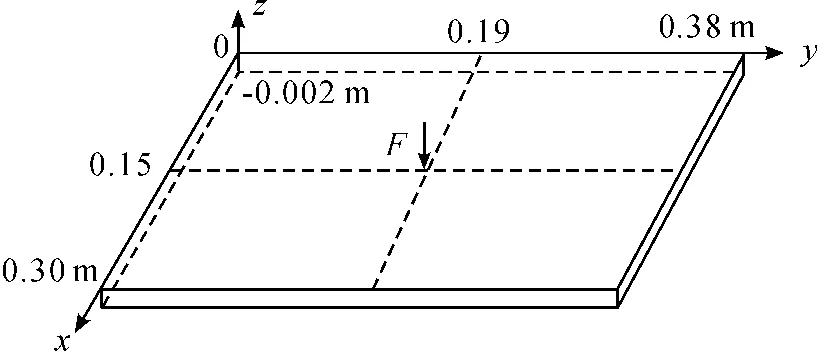
图1 矩形薄板

图2 矩形薄板的有限元模型

为验证编写Matlab程序的正确性，首先对四边简支板进行求解。将所求固有频率与精确的解析解和ANSYS结果做比较，如表1所示。随着有限元网格的不断细化，薄板各阶固有频率越来越接近其精确解，表明利用Matlab编写算法的收敛与合理性。

表1 四边简支矩形薄板的前8阶固有圆频率Hz

表2 四边固支矩形薄板的前8阶固有圆频率Hz

3.2 板表面声压分布

已知空气密度ρ0=1.225 kg/m3，声在空气中的传播速度为c0=343 m/s，激振力位于平板中心处，幅值为1 N，如图1所示。为减小计算量，计算时采用20×14网格。图3～6分别为不同激励频率下板的表面声压分布。从图中可以看出，在激励频率小于第1阶频率时，其辐射声压随激励频率增加而逐渐增大。在得到表面声压后，便可以计算声场空间中任一点的声压。

图3 f=10 Hz时板表面的声压分布

图4 f=20 Hz时板表面的声压分布

图5 f=30 Hz时板表面的声压分布

图6 f=40 Hz时板表面的声压分布

3.3 声辐射模态分析

图7～12分别是无量纲频率kl=0．1，0．5，1，2，5，10时平板的前4阶声辐射模态(kl=ka，k为波数且k=ω/c，a为板长)。

分析可得:当kl≤2时，矩形的各阶辐射模态图形随频率变化不大，辐射模态形状比较规则;随着频率的不断增加，辐射模态的形状变得越来越复杂。辐射模态在低频时具有的这种形状相似性，意味着在低频时，可以用某一频率的辐射模态代替某一频域范围内其他辐射模态;与结构的振动模态类似，形状规则结构的各阶辐射模态在xy平面内呈对称或反对称性，而且频率的影响并不会改变辐射模态的这种对称或反对称性。

图7 kl=0．1时板的前4阶声辐射模态形状

图8 kl=0．5时板的前4阶声辐射模态形状

图9 kl=1时板的前4阶声辐射模态形状

图10 kl=2时板的前4阶声辐射模态形状

图11 kl=5时板的前4阶声辐射模态形状

图12 kl=10时板的前4阶声辐射模态形状

4 结论

利用Matlab对薄板结构振动进行有限元分析，并通过瑞利积分求出板的表面声压，利用结构表面辐射阻抗阵求得板的声辐射模态。结果表明:基于Matlab软件编写的程序能快速方便地得到薄板结构的固有频率，计算结果能较好地收敛并达到满意的精度;当激励频率小于第1阶频率时，其辐射声压随激励频率增加而逐渐增大;辐射模态在低频时具有形状相似性，形状规则结构的各阶辐射模态在x-y平面内呈对称或反对称性，且不随频率的变化而改变。

［1］张波，沈火明，支伟.有限元/边界元法求解变厚度板的声辐射［J］.科学技术与工程，2010，10(36):8963 -8967.

［2］任惠娟，盛美萍.矩形薄板的模态声辐射效率［J］.机械科学与技术，2010，29(10):1397-1400.

［3］刘聪，姜哲.薄板结构辐射声功率及其灵敏度分析［J］.噪声与振动控制，2012(4):116-120.

［4］陈美霞，杜磊，陈乐佳.基于边界元法的平板结构声振性能数值计算［J］.武汉理工大学学报，2009，33(6): 1048-1051.

［5］黎胜.考虑流体加载效应的板结构声辐射损耗因子和辐射效率的计算分析［J］.中国舰船研究，2010，5(2): 9-13.

［6］黎胜，杨婧媛.水下加筋板振动的声辐射代理模型研究［J］.声学学报，2010，35(6):659-664.

［7］吴锦武，赵龙胜，黄凌志.基于分层理论的层合板结构声辐射模态传感器设计［J］.机械工程学报，2014，50 (3):116-122.

［8］张涛，姜哲.基于声辐射模态的板加筋位置优化［J］.科学技术与工程，2014，14(1):154-158.

［9］左曙光，魏欢，严新富.基于声辐射控制的板结构优化设计［J］.同济大学学报:自然科学版，2012，40(1):88 -92.

［10］孙超，赵德有.板声传输主动控制辐射模态控制方法研究［J］.哈尔滨工程大学学报，2010，30(1):8-14.

(责任编辑 刘舸)

Research on the Thin Plate’s Vibration and Acoustic Radiation Based on Matlab Software

ZHANG Yuan-yuan1，SHEN Huo-ming2
(1.School of Water＆Civil Engineering，Xinjiang Agricultural University，Urumqi 830052，China;2.School of Mechanics＆Engineering，Southwest Jiaotong University，Chengdu 610031，China)

The vibration of the rectangular lamina was analyzed by means of a program developed within MATLAB.Acoustic pressure was calculated through Rayleigh Integral，and by the theory of radiation mode.Different acoustic modes under different frequency were calculated and the distribution law was discussed.The results show that the program based on the Matlab software can be used to calculate conveniently and efficiently the natural frequency of the plate.The radiation pressure of the plate surface increases with the excitation frequency under low-frequency conditions.Radiation modes have the shape similarity in low-frequency.Each order radiation mode of structure was symmetry or anti-symmetry in x-y plane，and didn’t change with the alteration of frequency.

vibration analysis;plate;Matlab;finite element;acoustic radiation

TB532

A

1674-8425(2014)08-0034-05

10.3969/j.issn.1674-8425(z).2014.08.008

2014-05-06

牵引动力国家重点实验室开放课题资助(tb1305);新疆水利水电重点科学基金资助项目(xjzdxk)

张媛媛(1988—)，女，硕士，主要从事结构振动与控制研究;通迅作者沈火明(1968—)，男，博士，教授，主要从事结构振动与控制、噪声、力学数值仿真研究。

张媛媛，沈火明.基于Matlab板的振动响应与声辐射研究［J］.重庆理工大学学报:自然科学版，2014(8): 34-38.

format:ZHANG Yuan-yuan，SHEN Huo-ming.Research on the Thin Plate’s Vibration and Acoustic Radiation Based on Matlab Software［J］.Journal of Chongqing University of Technology:Natural Science，2014(8): 34-38.