运用主成分分析法的过程控制和诊断

肖枝洪，冉小华

(重庆理工大学数学与统计学院，重庆 400054)

运用主成分分析法的过程控制和诊断

肖枝洪，冉小华

(重庆理工大学数学与统计学院，重庆 400054)

针对控制过程中多变量的共线性，提出一种主成分质量控制方法，对化工中甲烷气体生产过程进行质量监控与诊断。首先运用在正常状态下所观测的13组样本数据建立过程控制模型，然后根据所建模型对在异常状态下观测的12组样本数据进行监控与诊断。结果表明:该方法能够及时地监测出故障并能准确查找出引起故障的过程变量。

主成分分析;故障监控与诊断;T2控制图

在工业生产过程中，经常会发生各种故障，影响产品质量，甚至会引起重大人员伤亡和财产损失。因此在工业生产中进行故障检测与诊断已成为当前控制理论研究的热点之一。工业生产系统一般都具有过程精确、建模困难、过程变量众多且相互间强耦合，并且在实际中存在各种随机因素的影响等特点，这就使得基于机理模型的诊断方法的应用极为不便［1］。因此，在实际工业生产过程中统计建模运用的较多，多元统计过程控制是比较常用的多元质量控制方法。该方法能够检测生产过程中的多个相关变量，通过诊断、寻找、消除异常因素，达到提高产品质量的目的。然而当前运用的多元统计过程控制技术存在的主要问题是:随着过程变量维数的增加，监控的复杂性急剧增加，而变量间严重相关时会给过程的诊断带来极大的困难，且监控效率极低［2］。为了克服多元统计过程控制的不足，就需要将降维的主成分分析方法与质量控制过程有机地结合起来，对此已有大量的研究。例如文献［3－4］将此方法分别运用于食品加工厂设备监控系统和大坝安全多测点数据监控得到很好的效果。在文献［5］中提出运用主成分原理的多元质量控制图来监测荫罩生产过程，根据得分综合值绘制出多元控制图来检测和控制生产过程，但不足的是:利用得分综合做出的多元控制图重叠了较多的原始数据信息，不能反映真实的生产过程情况。在此基础上，本文将运用主成分分析法进行多变量质量控制与诊断，但不同于文献［5］的是:建立了故障检测与诊断模型，通过对T2和Q(或SPE)统计量与其阈值的判断，进行系统的故障检测与诊断。

1 主成分分析理论

1.1 基本思想

主成分分析是将原始变量进行综合，找出影响某一质量问题的少数几个综合特性。这些综合过程特性是将原来多个过程进行线性组合，这样不仅保留了原始数据中的主要变量，并且消除了变量间的相关性，与原来的过程特性相比更优越，是将原来多个过程特性降维为少数几个具有代表性的过程特性的质量控制方法［2］。

1.2 主成分分析原理

设有n个样品，设每个样品的主成分模型［7］为:满足以下条件:

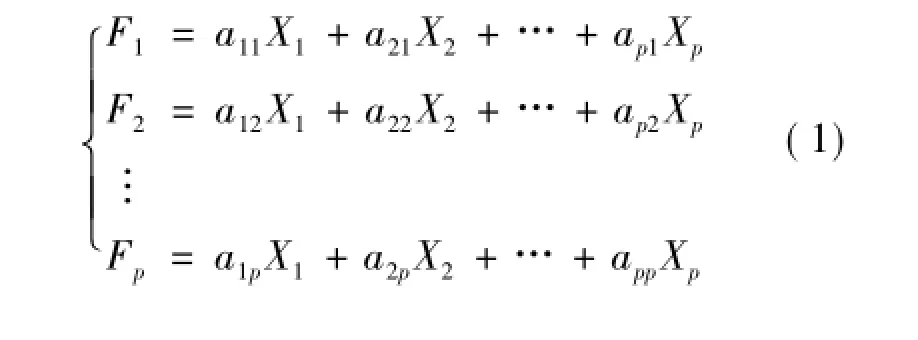
从代数观点看，主成分就是p个变量X1，…Xp的一些特殊的线性组合，在几何上这些线性组合将X1，…，Xp构成的坐标系旋转产生新坐标系，新坐标轴使之通过变差最大的方向(即说具有最大的样品方差)。

2 故障监控与诊断模型

基于主成分模型的多变量质量控制图［2］常有主成分SPE控制图、主成分T2控制图以及主成分贡献控制图。

假设多变量过程X=(X1，X2，…，Xp)'～N(μ，∑)的目标值为μ0，从中选取n个样本，记第i个样品的观测向量为X(i)=(Xi1，Xi2，…，Xip)'，n个样品组成的矩阵为Xn×p=(X(1)，X(2)，…，X(n))'。在进行主成分分析过程之前，应该先将原始数据标准化，即作如下标准化变换:

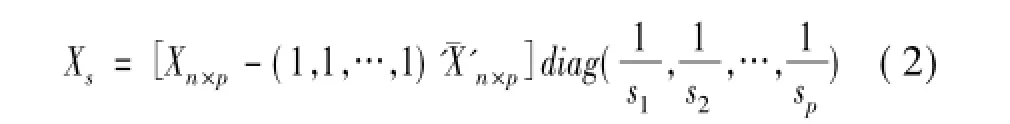
其中:¯X=(¯X1，¯X2，…，¯Xp)'为过程X的样本均值; si为Xi的样本标准差。

对标准化后的数据Xs进行主成分分析，可以得到Xs=t1u'1+t2u'2+…+tpu'p。假如用前m个(m＜p)主成分来代表原始数据中的主要变化，即可以得到如下主成分模型:

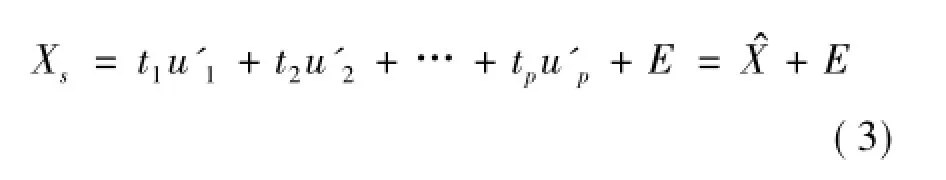
2.1 SPE控制图

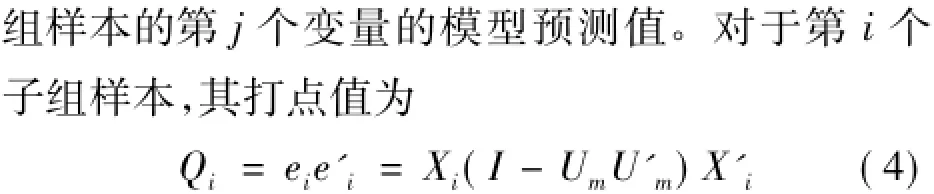
这里的ei是误差阵E的第i行，且Um=(u1，u2，…，um)。

其实统计量SPE在第i时刻的值只是一个标量，主要刻画的是第i时刻的过程观测值Xi与模型的偏离程度。因通过多个变量综合形成ei，所以SPE控制图可以对多变量过程X中的多个相关特性进行监控，这有别于其他一般的多变量质量控制。如取置信水平α，可以得到SPE控制图的控制线为:

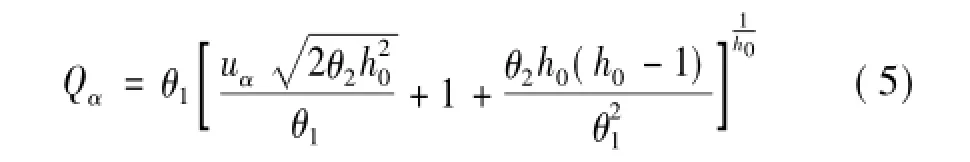
2.2 T2控制图

对于T2控制图，首先建立多变量过程X的主成分模型，然后通过计算T2统计量来对多个主成分进行监控。对于第i个子组样本X(i)，有统计量，其中:ti由主成分模型的第i个主成分的得分向量组成，Λm是由与前m个主成分所对应的特征值而组成的对角矩阵。主成分T2控制图主要通过模型内部的主成分向量模的波动来反映多变量过程X的变化情况。对于主成分模型的T2控制图的控制线可以表示为:

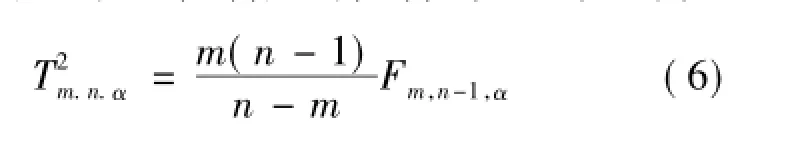
2.3 贡献控制图

当前面所计算的SPE统计量和T2统计量超出其控制线时，可以判定多变量X出现了不正常情况，但从上述的2种控制图中无法得知到底哪里出了问题。对此，贡献控制图的研究和发展可以解决这个问题。主成分贡献控制图可以分析每个过程分量对SPE统计量的贡献大小，并确定哪些过程分量引起了多维过程变量X的不正常变化情况。

通常，过程X的第i个子组样本的第j个分量对SPE统计量的贡献可以表示为Qij==(Xij－j)2，而第i个子组样本的第j个分量对第m个主成分的贡献为Xijumj，其中，umj是um的第j个元素。最后通过对X过程的各分量的主成分贡献控制进行分析，得知过程X的哪些分量的变化引起SPE统计量超出了控制线。

3 实例研究

本文针对中石化中甲烷液化气体的局部蒸馏过程X的输出建立多变量过程监控与诊断。蒸馏过程的好坏直接影响到甲烷气体的质量，然而对蒸馏过程效果不好评定，一般使用仪表板上的数据来检测整个过程的效果。本文选取塔顶的温度、入口的流速、塔顶回流的速度、再蒸馏的温度这4个过程变量作为主要检测数据指标。蒸馏过程X由下述变量构成:X1为塔顶的温度(℃);X2为入口的流速(L/h);X3为塔顶回流的流速(L/h);X4为再蒸馏的温度(℃)。

根据经验，塔顶的温度、入口的流速、塔顶回流的流速以及再蒸馏的温度的变动最能反映蒸馏过程的效果，从而影响气体质量;另外，设备或传感器的失效或故障所引起的偶然事件也需要及时报警和排除。因此，需要应用主成分质量控制方法对蒸馏过程实施统计监控，以便及时发现过程中的各种异常变化，并诊断出引起异常失控的原因。

对上述的4个变量过程进行监控，让生产过程正常运行一段时间。取正常运行阶段及故障阶段25个时刻(总100个数据)建立PCA模型，其中前13个时刻的样本点数据为正常运行阶段观测采集的，而后面12个时刻的样本点数据为故障阶段观测采集的。

3.1 主成分模型的建立

本文利用前13个时刻的样本点数据进行主成分分析［8］，首先对原始数据进行标准化处理，即可得到表1。

针对表1中的数据建立主成分模型，在此利用SAS软件进行主成分分析。经过运行程序［9］得到表2。

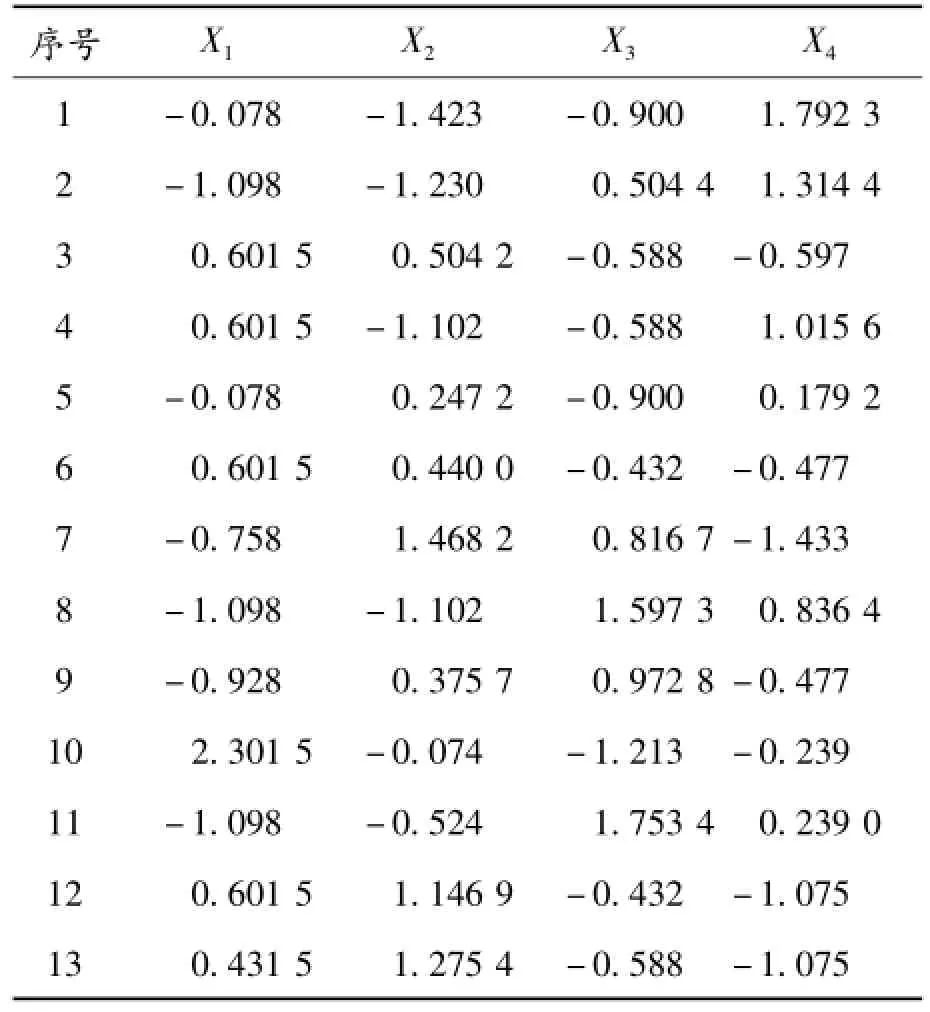
表1 实例中标准化后的数据

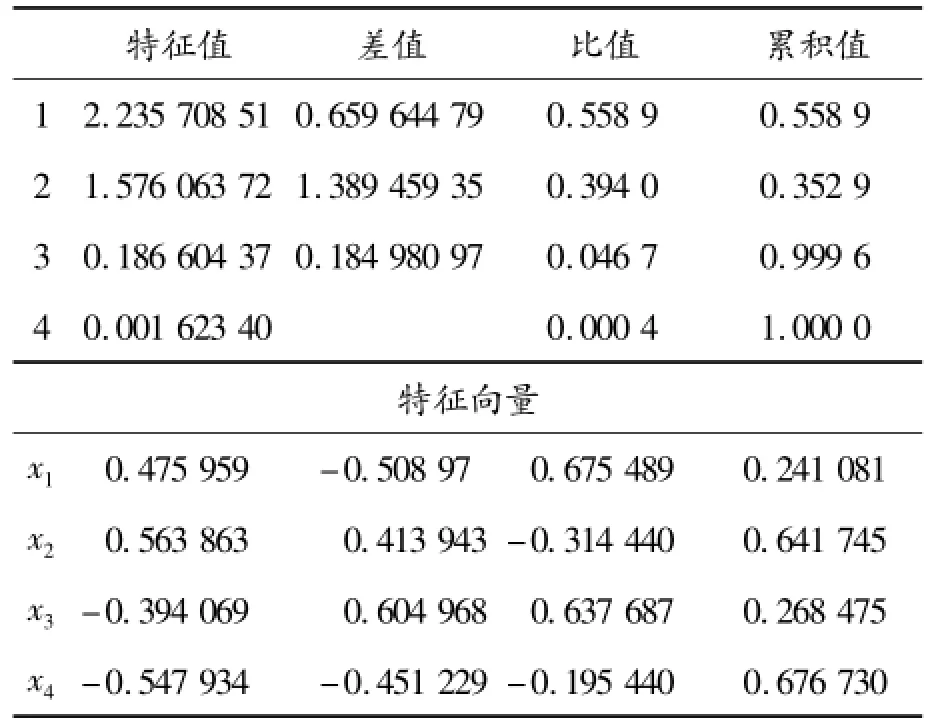
表2 相关阵的特征和特征向量

从表2可以看出:前2个主分量的累计贡献率达95.29%，远高于85%。因此，这里只需用前2个主分量就能更好地概括大部分信息。

根据表2可以得到负荷向量矩阵为:

在此，根据式(4)利用Matlab软件计算出主成分SPE控制图的Qi打点值见表3。

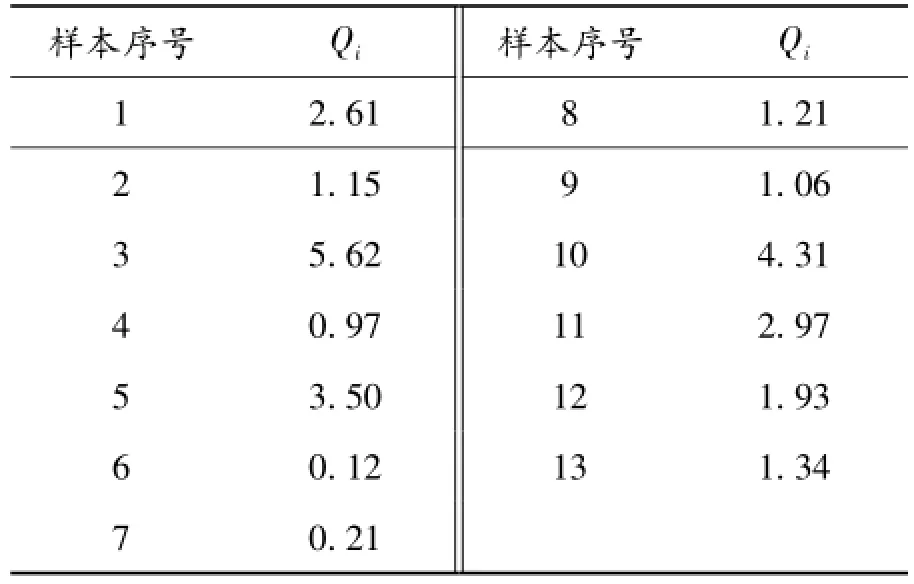
表3 主成分SPE控制图的打点值

从表2中可得4个特征值分别为λ1=2.235 7，λ2=1.576 1，λ3=0.186 6，λ4=0.001 6。

由此得出

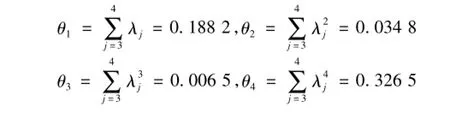
然后根据式(5)，给定置信水平α=0.01，有μ0.01= 2.325，由此可得

相应地，运用主成分控制研究的方法利用R软件绘制图1～3。从图1中可明显看出:第9、第7个样本点离第一主成分较近;第2、4、6、11样本点离第二主成分较近;第10个样本点偏离第一、第二主成分较远。

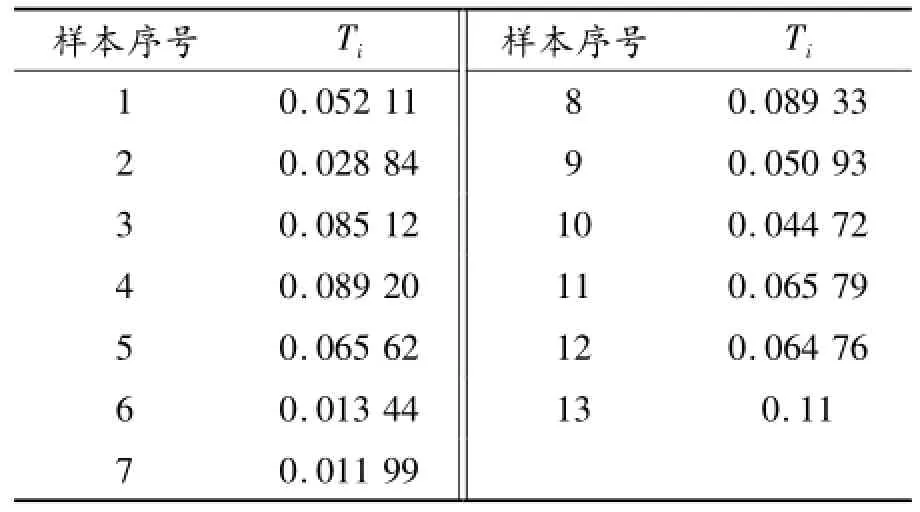
表4 主成分T2控制图的打点值

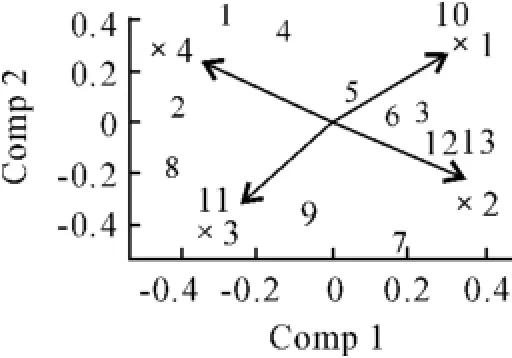
图1 原始数据分别在第一、第二主成分下的散点图

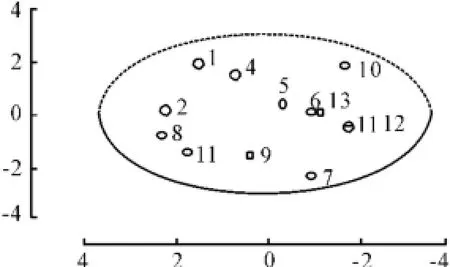
图2 原始数据主成分椭圆质量控制图

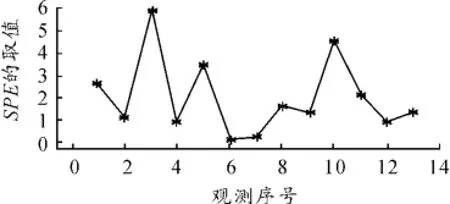
图3 原始数据的SPE控制图

在此绘制出主成分椭圆控制图和SPE控制图来检测原始数据的观测值是否都处于受控状态。从图2可明显看出:原始数据值都在控制限内。由图3可知:13组Qi点都落在控制线内，所以可认为多变量蒸馏过程X处于统计受控状态，所建立的主成分模型有效，于是可以用Qα作为控制用控制图的控制线，用于故障监控与诊断。

3.2 故障监控与诊断

现在不仅已知13组原始数据都处于受控状态，还可认为所建立的主成分模型成立可用于监控。为了找出12组失控的新观测值，可通过本文建立的主成分模型来检测，从而确定引起的失控的变量。

通过Matlab软件绘制出控制图，见图4、5。

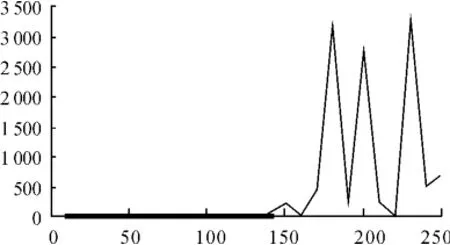
图4 对应于监测的SPE控制图

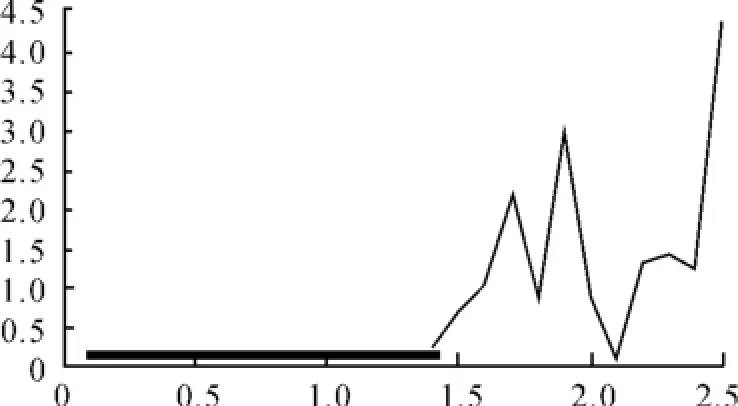
图5 对应于监测的T2控制图

图4(粗线代表控制线，细线代表新观测值的SPE)和图5(粗线代表控制线，细线代表新观测值的T2)分别是新采集的12组观测数据的SPE控制图和T2控制图。对于图4、5的控制线分别为UCL=Q0.01=5.99和UCL=T2=0.130。很容易看出:在后面提供的12组样本点中，从第14个采样时刻点开始，Q统计量以及T2统计量都严重超出了其控制线。在图4、5中，因图形尺度的关系，Q统计量以及T2统计量的控制限均与横坐标重合，所以可判定过程出现异常，表现在第20个采样时刻点远远偏离了由前面数据所建立的主成分模型，因此，在该点上绘制变量的主成分贡献图见图6。

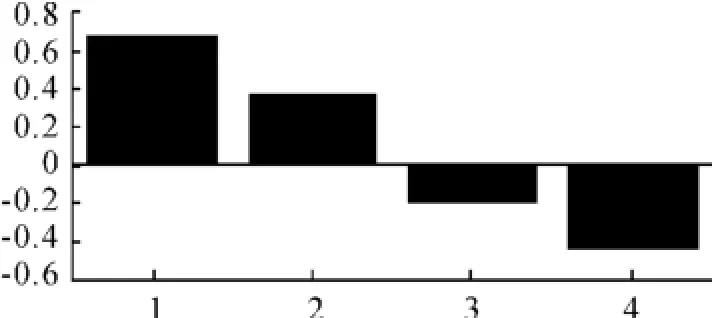
图6 第20时刻样本点的主成分贡献图

图6表示了各个过程变量在第20个采样时刻对前2个主元的贡献图。由于变量的变化程度与相对应的主元负荷一起决定每个变量对主元的贡献图，则从图6可以看出:第1个变量即塔顶的温度和第4个变量即再蒸馏的温度对前2个主元的贡献最大。所以有理由判定在蒸馏过程中出现异常与塔顶的温度有很大关系。结合实际工业生产过程知:在蒸馏过程中塔顶温度异常是由塔顶回流引起的，所以要降低回流温度，以防引起塔顶温度失控，影响整个生产过程。

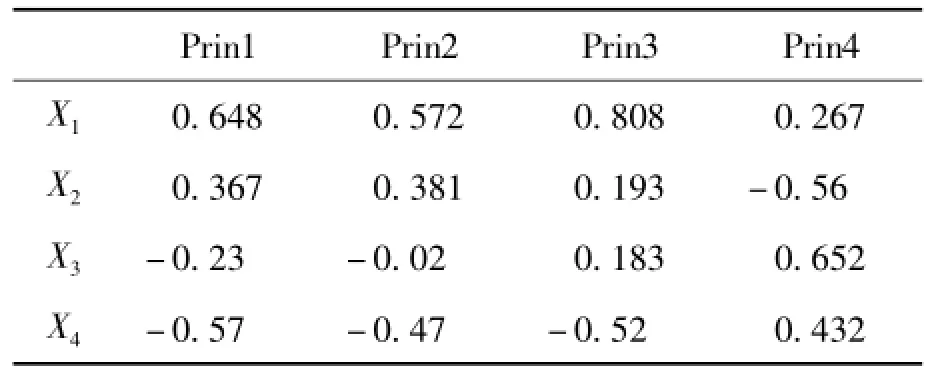
表5 主元和变量间的相关系数

表5为输出主元与各个变量间的相关系数。以主元Prin1为例，由表5可以看出:该主元与第1和第4个变量(即塔顶的温度和再蒸馏的温度)密切正相关，因此可以用温度来解释该主元。

4 结束语

本文将主成分质量控制方法用于实际甲烷气体生产过程中的监控诊断，能够及时判断生产过程中的异常情况，并精确查找出引起异常情况的过程变量［10］。本文利用主成分质量控制对工业生产过程进行质量监控，取得了较好的效果。一方面为该方法基于统计降维思维的过程控制和诊断提供了新的思路［11］;另一方面也为解决工业生产质量监控提供了一种新的方法和方向。

与常用多变质量控制方法相比，主成分分析法在质量控制监测过程中更加有效、精确。其不足之处在于:当多个过程变量出现异常时，该方法则不理想，甚至出现错误结论，对此还需进一步研究。

［1］李伯奎，刘远伟.表面粗糙度理论发展研究［J］.工具技术，2004，38(1):63－67.

［2］蒋家东，冯允成.统计过程控制［M］.北京:中国质检出版社，2011.

［3］杜福洲，唐晓表.基于PCA的多元质量控制与诊断方法研究［J］.制造业自动化，2006，28(8):10－18.

［4］陈瑞兴，程琳.基于PCA和多元控制图的大坝安全多测点数据监控方法［J］.水利与建筑工程学报，2012，10(5):68－73.

［5］耿修林.基于主成分原理的多元质量控制的构造［J］.数理统计与管理，2007，26(1):106－111.

［6］陈勇，梁军，陆浩.基于PCA的多变量控制系统的故障检测与诊断［J］.工程设计学报，2002，9(5):257－260.

［7］肖枝洪，余家林.多元统计及SAS应用［M］.武汉:武汉大学出版社，2013.

［8］苏理云，邓燕，冉雪竹，等.低合金高强度钢力学性能与化学成分之间的统计建模与分析［J］.重庆理工大学学报:自然科学版，2009，23(2):36－40.

［9］杜福洲，唐晓青.基于PCA的多元质量控制与诊断方法研究［J］.制造业自动化，2006，28(8):10－13.

［10］骆顺志，程越，李鑫.机械电子控制金属带式变速器速比控制及仿真［J］.重庆理工大学学报:自然科学版，2011，25(8):120－126.

［11］Evan L R，Leo H.Fault detection in industrial:Processes using canonical varitae Analysis and dynamie principal component analysis［J］.Chemo metries and Intelligent－Laboratory Systems，2000，51(8):81－93.

(责任编辑 刘舸)

XIAO Zhi－hong，RAN Xiao－hua

(School of Mathematics and Statistics，
Chongqing University of Technology，Chongqing 400054，China)

To the deficiencies of commonly usedmultivariate statistical process control，the principal component quality controlmethod is put forward to proceed quality monitoring and diagnostics on the production process of practical industrial methane gas.First，the process control model was established using the first13 groups of sample datawe observed in the normal state.Then，we used the establishedmodel to proceed qualitymonitoring and diagnostics on the known 12 groups of sample data we observed in the abnormal state.The results show that themethod can monitor the fault timelier and find out the process variables that causemalfunction accurately.

principal component analysis(PCA);fault detection and diagnosis;controlling figure of T2

TP273

A

1674－8425(2014)01－0096－06

10.3969/j.issn.1674－8425(z).2014.01.019

2013－09－07

重庆市科委资助项目(cstc2012jjA00018);重庆市教委项目(KJ130810)

肖枝洪(1965—)，男，博士，教授，主要从事工程概率、可靠性理论等方面研究。

肖枝洪，冉小华.运用主成分分析法的过程控制和诊断［J］.重庆理工大学学报:自然科学版，2014(1):96－101.

format:XIAO Zhi－hong，RAN Xiao－hua.Monitoring and Fault Diagnosis Based on PCA Method［J］.Journal of Chongqing University of Technology:Natural Science，2014(1):96－101.

Monitoring and Fault Diagnosis Based on PCA M ethod