Matlab/Simulink环境下单电磁铁悬浮系统的3种PID仿真
宋荣荣,马卫华
(1.西南民族大学计算机科学与技术学院,成都 610041;
2.西南交通大学牵引动力国家重点实验室,成都 610031)
Matlab/Simulink环境下单电磁铁悬浮系统的3种PID仿真
宋荣荣1,马卫华2
(1.西南民族大学计算机科学与技术学院,成都 610041;
2.西南交通大学牵引动力国家重点实验室,成都 610031)
由于轨道不平顺变化会对悬浮系统有影响,选择适合于单电磁铁悬浮系统的PID控制仿真方法是悬浮控制系统设计中的一个很重要的问题。基于单电磁铁悬浮系统的数学模型,提出了3种PID控制仿真方法。利用Matlab/Simulink中的工具箱,通过仿真验证了3种PID控制系统的可行性。结果表明:与方法1和方法2相比,基于S函数的方法3对轨道低频振动能实现有效地跟踪,且对轨道高频振动具有较强的抑制能力。该研究成果为解决单电磁铁悬浮系统的轨道不平顺问题提供了一种较好的仿真方法。
单电磁铁悬浮系统;轨道不平顺;PID控制;Matlab仿真
如何克服轨道干扰是悬浮控制系统设计中的一个很重要的问题[1]。轨道的低频和高频干扰会导致单电悬浮系统的特性参数或结构发生改变,使控制系统品质指标无法保持在最佳范围内[2-3]。控制效果的好坏取决于辨识模型的精确度,这对PID控制的仿真方法提出了更高的要求[4]。因此,有必要比较PID控制的不同仿真方法,从而选择适当的仿真方法研究单电磁铁悬浮系统的悬浮性能。
现有的仿真方法主要有采用状态方程描述系统进行仿真、采用传递函数描述系统进行仿真、采用S函数描述系统进行仿真[5]。这些仿真方法各有利弊。其中,用S函数很容易表示复杂的被控对象及控制算法,特别适合于复杂系统的仿真。它允许采用C、C++、FORTRAN等语言进行编写,结合了Simulink框图图形化的特点和Matlab编程灵活方便的优点,增强和扩展了Simulink的强大机制[6]。采用S函数仿真的也是近年来普遍采用的仿真方法之一[7-8]。
本文先建立单电磁铁悬浮系统的数学模型;然后提出3种PID仿真方法;最后基于Matlab/ Simulink的工具箱,对轨道不平顺进行仿真研究。研究结果表明:基于S函数的仿真方法对轨道干扰具有较好的抑制效果。
1 悬浮系统模型
单电磁铁悬浮系统结构如图1所示。假设电磁铁不仅在垂直方向运动,还沿轨道以速度v运行。
图1中:绝对气隙z(t)为磁极表面与绝对参考平面的距离;h(t)为轨道面与绝对参考平面的距离;相对气隙c(t)为磁极表面与轨道面的气隙。加速度计所测得的输出为加速度¨z(t);气隙传感器测得的输出为相对气隙c(t);i(t)为电流互感器测得的控制线圈电流;u(t)为绕组回路的电压。
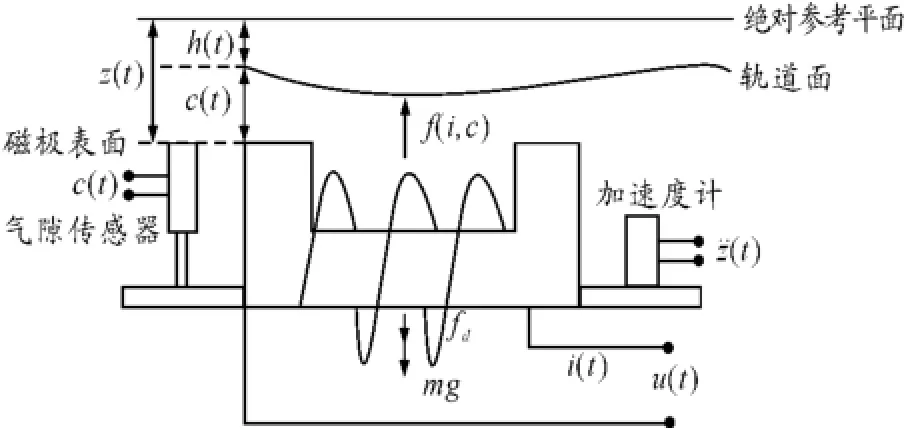
图1 单电磁铁悬浮系统结构
设N为电磁铁线圈的匝数,A为磁极面积,R为线圈的电阻,μ0为空气磁导率,mg为电磁铁重力,F(i,c)为悬浮电磁力,fd(t)为外界干扰力。
在分析单电磁铁悬浮系统的动力学模型时,假设[9]:①忽略漏磁的影响;②忽略磁铁芯和导轨中的磁阻,磁势均匀降落在气隙c(t)上;③电磁铁仅有垂直方向上的移动,其他方向受限无运动。
根据电磁学和动力学理论,得到基于绝对参考平面的单电磁铁动态模型方程
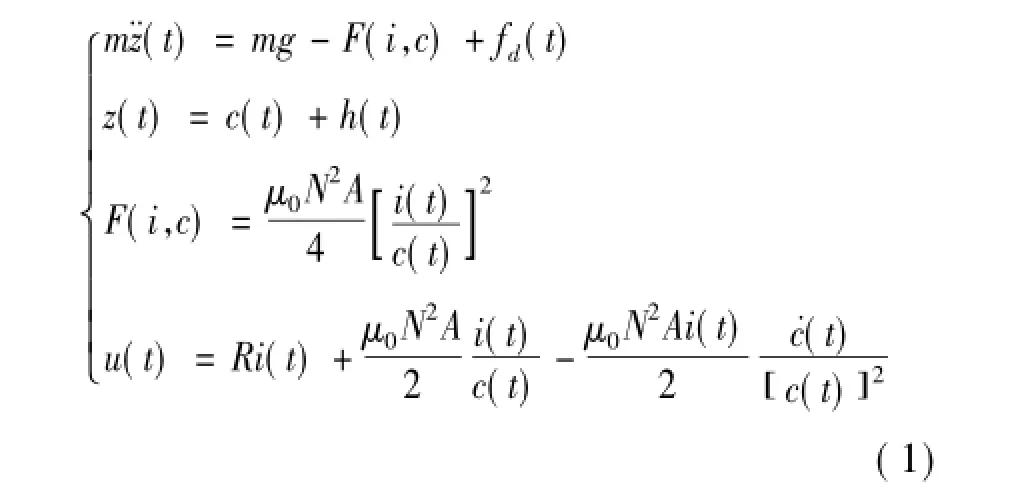
其中,平衡点的边界条件为
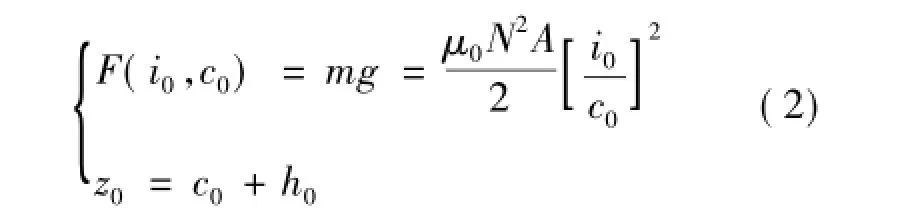
在平衡点(i0,c0)附近进行线性化处理,可以得到状态方程
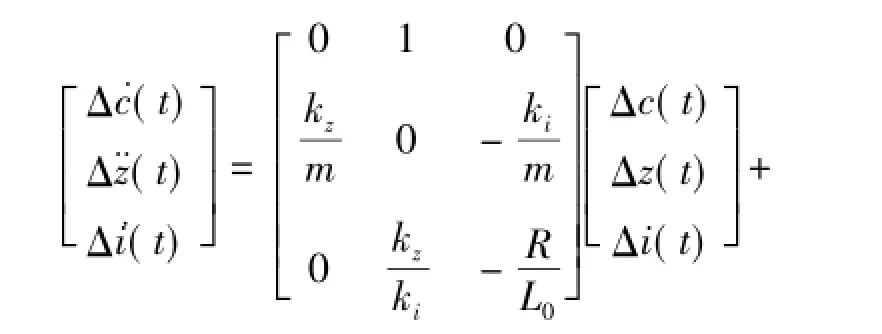

由劳斯(Routh)判据知:这是一个二阶不稳定系统,为使电磁铁稳定悬浮必须采取反馈控制。
2 3种PID控制仿真方法
对系统方程(4)增加一个状态变量∫c(t)d t,以电流为控制变量,则得到开环系统的状态方程
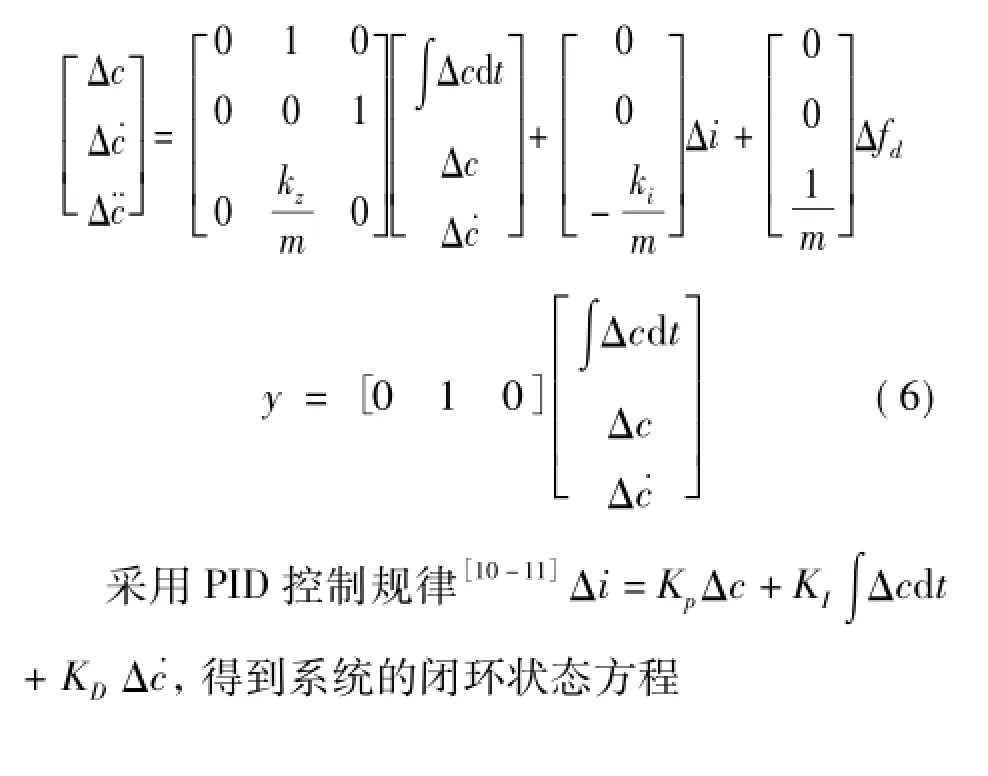

期望的闭环传递函数为

比较闭环特征方程(8)和期望的闭环传递函数(9),可求得参数Kp=19 638.65,KI=603 880.52,KD=215.68。
2.1 仿真方法1
采用传递函数描述被控系统,在Simulink下进行仿真。仿真结构如图2所示。
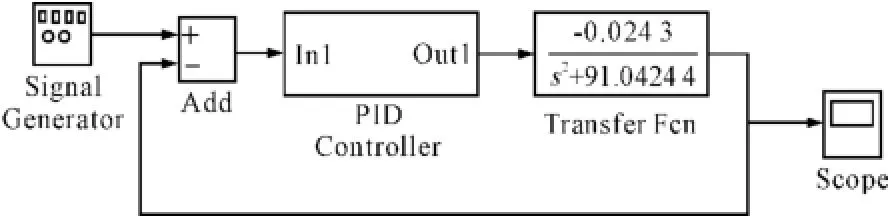
图2 PID控制的仿真结构1
PID控制器的内部结构如图3所示。
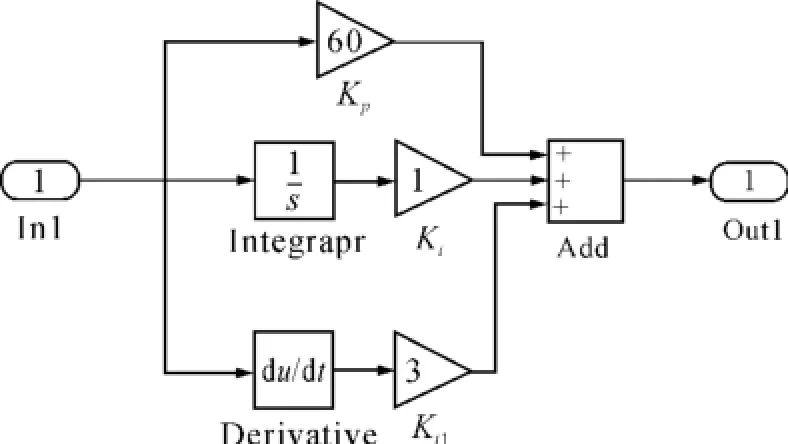
图3 PID控制器的内部结构
2.2 仿真方法2

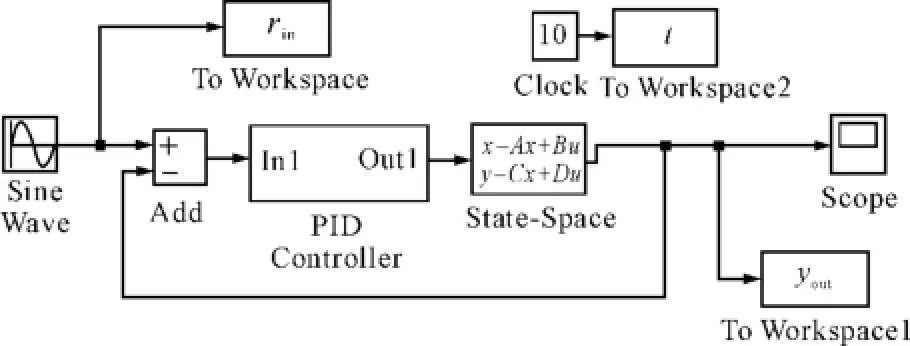
图4 PID控制的仿真结构2
2.3 仿真方法3
采用S函数可实现在Simulink下复杂控制器和复杂对象的编程。本文利用S函数实现对被控对象的表达、控制的设计及仿真结果的输出。
在S函数中,采用sizes结构进行初始化,选择1个输出,3个输入分别为P、I、D。系统初始状态为x(0)=0,˙x(0)=0。仿真结构如图5所示。
3 M atlab仿真分析
计算机仿真软件采用Matlab中的Simulink[13],验证模糊自整定PID控制器的性能。单电磁铁悬浮控制系统的参数如表1所示。
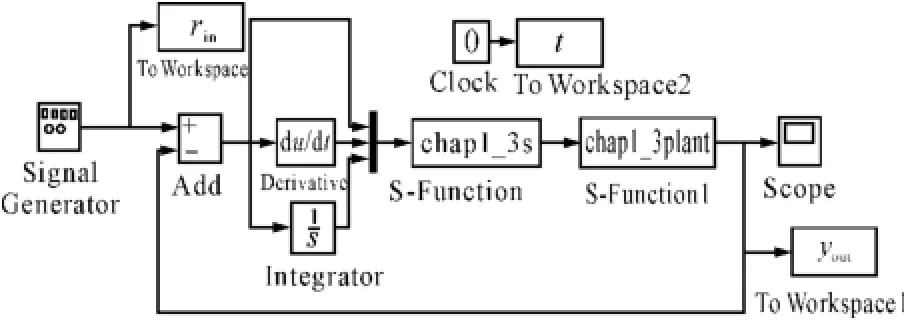
图5 PID控制的仿真结构3
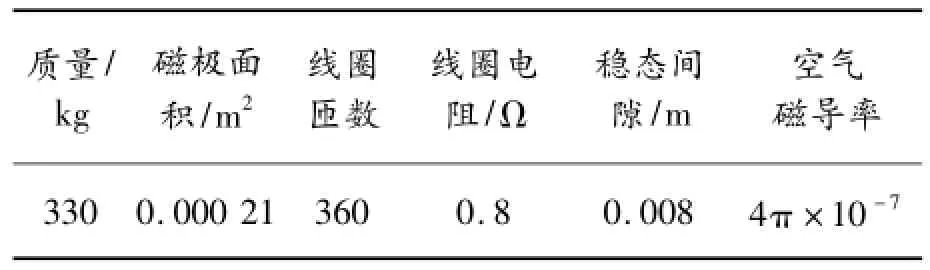
表1 单电磁铁悬浮系统的参数
3.1 轨道低频扰动的抑制性能
设轨道不平顺的低频扰动所对应的正弦波信号的幅值为5 mm,振动频率为0.1 Hz。仿真结果如图6(a)~(c)所示。
3.2 轨道高频扰动的抑制性能
设轨道不平顺的高频变化所对应的正弦波信号的幅值为5 mm,振动频率为10 Hz。3种仿真方法的仿真结果如图7(a)~(c)所示。

图6 对轨道低频扰动的跟踪性能
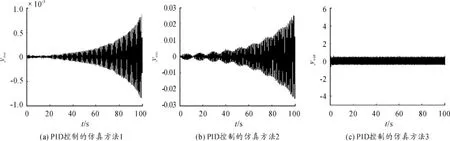
图7 对轨道高频扰动的抑制性能
4 结论
由于单电磁铁悬浮系统具有非线性特性,本文先建立该系统的状态方程;然后以电流为控制量,设计3种PID控制仿真方法;最后,基于Matlab软件进行验证。结果表明:
1)由于轨道不平顺对悬浮系统的影响,悬浮系统的控制性能对PID的控制参数有很强的依赖性。因此要克服轨道干扰,就必须选择适当的仿真方法以获得系统最佳的控制特性。基于S函数的仿真方法3可以准确地描述复杂系统和控制算法。
2)对于轨道的低频扰动和高频扰动,基于S函数的仿真方法与前2种仿真方法相比具有较强的抑制性能。上述结果表明:该仿真方法能够更好地解决轨道不平顺问题。
3)今后将考虑如何将仿真方法3和智能控制结合,更好地应用到磁悬浮控制中去,这是本研究的最终目的。
[1]张耿,李杰,杨子敬.低速磁浮轨道不平顺功率谱研究[J].铁道学报.2011,33(10):73-78.
[2]Zhiqiang Long,Guohua Shi,Lianchun Wang.Suspension influence analysis of track irregularity of maglev train[C]//Control and Decision Conference.[S.l.]:[s. n.],2010:942-947.
[3]Zheng Shubin,Lin Jianhui,Lin Guobin.Long-wave irregularity detection of high-speed maglev track[C]//Electronic Measurement and Instruments.[S.l.]:[s.n.],2007:277-281.
[4]ZhaiWanming,He Zhenxing,Song Xiaolin.Prediction of high-speed train induced ground vibration based on traintrack-ground system model[J].Earthquake Engineering and Engineering Vibration,2010,9(4):545-554.
[5]贾秋玲.基于MATLAB7.X/SIMULINK/STATEFLOW系统仿真、分析及设计[M].西安:西北工业大学出版社,2006.
[6]李颖,朱伯立,张威.Simulink动态系统建模与仿真基础[M].西安:西安电子科技大学出版社,2004.
[7]任永峰,安中全,李含善.基于S函数的并网型交流励磁双馈电机风力发电系统研究[J].太阳能学报,2009,30(10):1401-1407.
[8]姚文冰,姚天任.语音编/解码仿真中S函数的设计与应用[J].华中科技大学学报:自然科学版,2001,29 (5):83-85.
[9]谢云德,常文森.电磁型(EMS)磁悬浮列车系统铅垂方向的建模与仿真[J].铁道学报,1996,(4):47-54.
[10]陶永华.新型PID控制及其应用[M].北京:机械工业出版社,1998.
[11]栾军山,陈华.Smith-模糊PID在过程控制中的应用[J].重庆理工大学学报:自然科学版,2010,24(7): 106-109.
[12]郑大钟.线性系统理论[M].北京:清华大学出版社,2002.
[13]张智星.Matlab程序设计与应用[M].北京:清华大学出版社,2002:360-365.
(责任编辑 刘舸)
Three PID Simulation of the Single M agnetic Levitation System Based on M atlab/Simulink
SONG Rong-rong1,MAWei-hua2
(1.College of Computer Science and Technology,Southwest University for Nationality,Chengdu 610041,China;2.State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China)
Due to the impact of the track irregularity on suspension system,selecting the suitably PID control simulationmethod for single electromagnet levitation system is a very important problem in the design of the suspension control system.In this paper,the mathematicalmodel of singlemagnet suspension system is based on PID control,and this paper puts forward three kinds of simulation methods.By using of Simulink toolbox in Matlab,the simulation verifies the feasibility of three kinds of PID control system,and the simulation results show that the third simulationmethod based on S function can more effectively realize the low frequency vibration of track,and have stronger suppression ability to the high frequency vibration of track,compared to the first simulationmethod and the secondone.In this paper,a better simulation method is provided for solving the single electromagnet levitation system of track irregularity problem.
singlemagnetic levitation system;track irregularity;PID control;Matlab simulation
TP13
A
1674-8425(2014)01-0007-05
10.3969/j.issn.1674-8425(z).2014.01.002
2013-09-27
西南民族大学中央高校专项资金资助项目(12NYZQN19);国家自然科学基金资助项目(51005190);四川省科技支撑计划项目(2012GZ0103)
宋荣荣(1979—),女,博士研究生,副教授,主要从事泛函分析方面的研究。
宋荣荣,马卫华.Matlab/Simulink环境下单电磁铁悬浮系统的3种PID仿真[J].重庆理工大学学报:自然科学版,2014(1):7-11.
format:SONG Rong-rong,MA Wei-hua.Three PID Simulation of the Single Magnetic Levitation System Based on Matlab/Simulink[J].Journal of Chongqing University of Technology:Natural Science,2014(1):7-11.

