柯式公式的迭代法求解研究
王争利,覃彦福 (长江大学工程技术学院城市建设系,湖北荆州 434020)
柯式公式的迭代法求解研究
王争利,覃彦福 (长江大学工程技术学院城市建设系,湖北荆州 434020)
在雷诺数Re=232149.5,相对粗糙度K/d=0.000966的条件下,给出实际工程常用区间范围[0.008,0.1]的柯列波洛克-怀特公式数学特性曲线,为采用迭代方法计算摩擦阻力系数提供依据。分别对柯列波洛克-怀特公式及其4个不同变形公式能否适用于迭代计算进行比较分析,使用二分法和黄金分割法对适用于迭代的变形公式进行MATLAB编程计算,计算显示在适合迭代的公式中,公式的形式对迭代结果、迭代步数、迭代时间没有影响。
柯列波洛克-怀特公式;迭代计算;二分法;黄金分割法
利用柯列波洛克-怀特公式(简称柯式公式)可以计算工业管道紊流三区的摩擦阻力系数(又称为摩擦因子、沿程阻力系数),从而计算管道的阻力,在采暖、空调及燃气工程中应用广泛,文献[1]用柯式公式计算了钢管内热水的摩擦阻力系数,并编制40~90℃间隔10℃水力计算表;同时也将其用于计算紊流过渡区空调水系统开式管网与闭式管网的摩擦阻力系数,编制空调水力计算表。文献[2]依据柯式公式及其改进公式编制了3类9种常用风管的水力计算表。《城镇燃气设计规范》(GB50028-2006)推荐燃气管道摩擦阻力系数λ按柯氏公式计算:
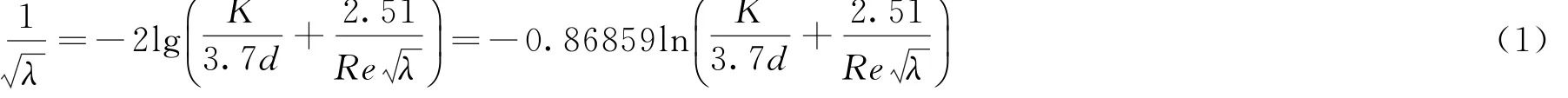
式中,K为管壁内表面的当量绝对粗糙度,mm;d为管道内径,mm;Re为雷诺数。
许多学者[3~7]就自己所从事的工程领域,尤其是燃气工程领域利用不同的方法对柯氏公式进行求解,以获得摩擦阻力系数计算阻力损失,不同作者使用的计算方法不同,迭代法以二分法、牛顿法为主,少数作者[8]用到了牛顿迭代法的改进方法——弦割法,总的来看,计算方法比较单一,注重应用,只计算出结果,并未对其计算方法本身进行深入探析。为此,笔者对柯式公式及其4个不同变形公式进行了比较分析,使用二分法和黄金分割法对适用于迭代的变形公式进行MATLAB编程计算。
1 几点说明
限于篇幅,特对分析条件、对比条件、迭代过程、收敛条件、计算算例作如下说明:
1)无论采取哪种方法,迭代的范围处在[0.008,0.1],其依据是文献[1]提供的莫迪图;收敛的最小值取ε=10-6,将条件统一,便于不同方法之间的比较。
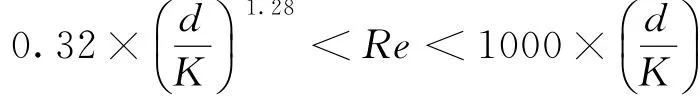
3)判断迭代效率的依据除了时间外,还增加了每一种迭代算法的迭代次数,用于比较计算结果与效率。
4)编程使用MATLAB6.5.1,在相同条件下运行程序。
5)笔者所使用的计算方法,可参阅文献[10-11]。
2 柯氏公式的数学特性分析


图1 f1与f2曲线
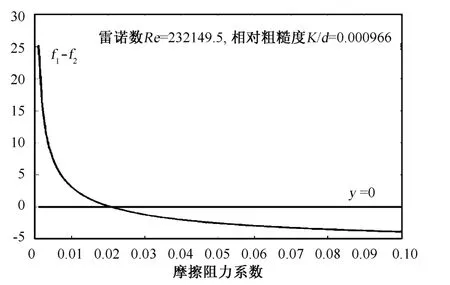
图2 柯式公式变形公式函数曲线
3 柯式公式的变形式及迭代分析

在0.008~0.1(摩擦阻力系数)范围内对式(3)~式(6)进行分析,图3为式(3)~式(5)右边项函数曲线及斜率为1的直线即y=x。由文献[10]提供的基本迭代过程的几何曲线,直接排除式(5),其原因是其变形后突然增加一个解。图4是式(6)右边项在区间[0.008,0.025]的函数曲线,由图4可以看出式(6)同式(5)一样也是2个解,但式(6)有一个解是0,在物理上和编程上都很容易排除,故式(6)可以用于迭代计算。

图3 公式(3)~(5)右边项的函数曲线
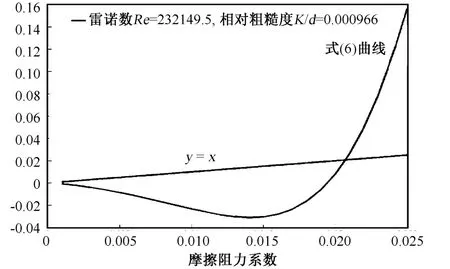
图4 柯式公式变形公式(6)函数曲线
4 柯式公式的迭代计算与结果分析
针对式(2)分别采用二分法、黄金分割法求解,其迭代过程框图如图5、图6所示;式(3)、(4) 和(6)的迭代过程与之类似,这里不重复框图。二分法、黄金分割法计算结果列于表1、表2并与阿氏公式的计算结果进行比较。

图5 二分法对柯氏公式(2)的迭代框图

图6 黄金分割法对柯氏公式(2)的迭代框图

表1 对柯氏公式用二分法迭代计算摩擦阻力系数的结果

表2 对柯氏公式用黄金分割法迭代计算摩擦阻力系数的结果
由表1和表2可以明显看出,尽管方程形式不同,迭代方法不同,但迭代时间和迭代结果相对于阿氏公式计算结果的相对误差基本相同且相对误差十分小,计算结果的精度均满足工程要求。柯氏公式的变形形式除了本身不适合迭代的式(5)外,公式的变形式(2)~(4)和式(6)对迭代结果、迭代步数、迭代时间,影响不大;二分法对式(2)~(4)和式(6)迭代结果、迭代步数是完全相同的,迭代时间接近,黄金分割法也是如此,但二分法的计算误差及迭代步数明显小于黄金分割法。
5 结论
对柯氏公式的4种变形式进行迭代分析,并在[0.008,0.1],雷诺数Re=232149.5,相对粗糙度K/d=0.000966的条件下,对相应的公式进行了迭代求解,将迭代结果与阿氏公式进行比对,得出结论如下:
1)柯氏公式的4种非恒等变形式(3)~(6)中,除式(5)不能迭代计算外,其余均适合于迭代计算;
2)柯氏公式适合于迭代的变形式(2)~(4)和式(6),公式变形形式对迭代步数、迭代结果影响不大,但迭代方法对迭代影响较大,黄金分割法在收敛速度上明显略于二分法,若进行大量运算所需计算时间必然要长;
3)无论是二分法还是黄金分割法求解摩擦阻力系数,其求解结果均能满足工程需求。
[1]陆耀庆,唐世杰,季伟,等.《实用供热空调设计手册》[M].第2版.北京:中国建筑工业出版社,2008.
[2]中国建筑标准设计研究院.国家建筑标准设计图集08K508-1《通风管道沿程阻力计算选用表》[M].北京:中国计划出版社, 2008:2-8.
[3]董哲生.流体在工业管道中流动沿程阻力计算的研究[J].江西能源,2006(3):26-27.
[4]齐清兰,杨秋新.柯列波洛克公式中沿程阻力系数的计算方法[J].河北水利水电技术,1998(4):17-18.
[5]江山,张海金,齐鹏.关于管道沿程阻力系数问题的分析[J].黑龙江水利科技,2012,40(10):177-188.
[6]蒋降龙.燃气管道摩擦阻力计算的探讨[J].煤气与热力,2004,24(1):37-40.
[7]姜东琪,杜建梅,史宇倩,等.柯氏公式摩擦阻力因素和庭院燃气管道的计算[J].煤气与热力,2004,24(3):152-154.
[8]刘洋.柯列波洛克公式几种常用求解方法的比较[J].计算机教学,2003(5):128.
[9]汪兴华.工业管道紊流三流区的划分标准[J].衡阳工学院学报,1994,8(2):59-65.
[10]徐长发,王邦.实用计算方法[M].第2版.武汉:华中科技大学出版社,2009.
[11]熊国武.基于MATLAB的微灌系统水力计算程序设计及工程应用[D].西安:西安建筑科技大学,2007.
[编辑]洪云飞
O241
A
1673-1409(2014)19-0019-04
2013-11-04_
王争利(1982),男,硕士,讲师,现主要从事建筑环境与能源应用方面的教学与研究工作。

