Taylor公式在一类级数敛散性判断中的应用
2014-06-27 05:48杜厚维陈忠长江大学一年级教学工作部湖北荆州434025
长江大学学报(自科版) 2014年19期
杜厚维,陈忠 (长江大学一年级教学工作部,湖北荆州 434025)
Taylor公式在一类级数敛散性判断中的应用
杜厚维,陈忠 (长江大学一年级教学工作部,湖北荆州 434025)
对一类不满足莱布尼兹判别法的交错级数,利用Taylor公式将其一般项进行分离,然后基于各分解项的敛散性判断原级数的敛散性,最后利用算例说明该方法的有效性。
Taylor公式;数项级数;敛散性
对于交错级数敛散性的判断,《高等数学》课程重点介绍了莱布尼兹定理[1-3],而对于不满足莱布尼兹定理条件的交错级数,往往用级数收敛的定义或借助绝对收敛来判断。下面,笔者将运用Taylor公式判断一类具有某种结构的交错级数的敛散性。
1 基本概念

2 主要结论

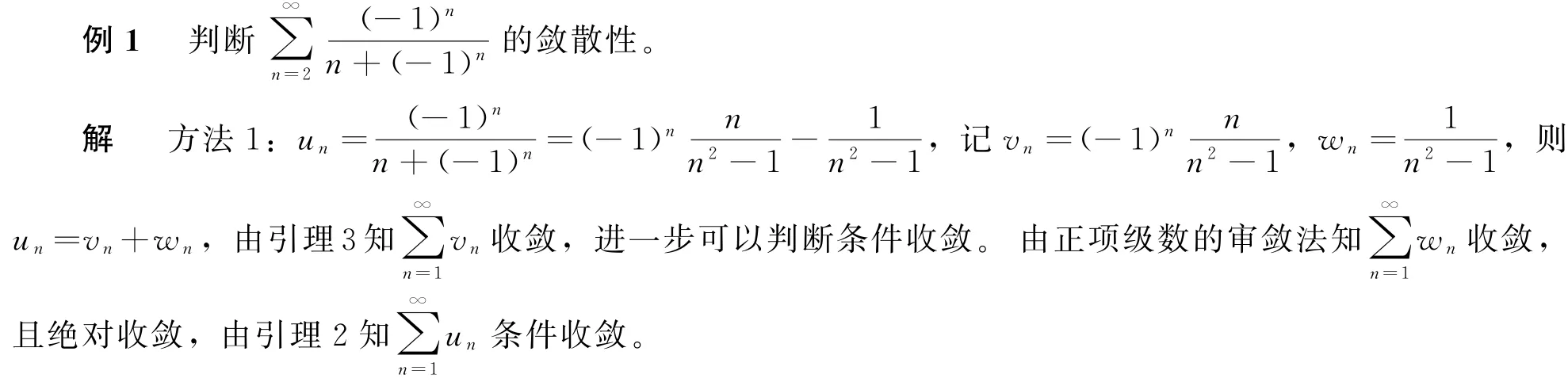
3 算例

4 结语

[1]郑玉敏.一类交错级数敛散性的探讨[J].高等数学研究,2001(4):11-12.
[2]同济大学.高等数学[M].北京:高等教育出版社,2001.
[3]毛京中.高等数学学习指导[M].北京:北京理工大学出版社,2001.
[编辑]张涛
O171.2
A
1673-1409(2014)19-0014-03
2014-02-23
国家自然科学基金资助项目(11201039;61273179);湖北省教育厅重点项目(D20101304)。
杜厚维(1978-)男,硕士,讲师,现主要从事应用泛函分析方面的教学与研究工作。
猜你喜欢
数学物理学报(2022年1期)2022-03-16
——基于F省H医院的案例分析
社会工作与管理(2020年5期)2020-10-19
华东师范大学学报(自然科学版)(2019年3期)2019-06-24
湘潮(上半月)(2019年1期)2019-05-22
西安工程大学学报(2016年2期)2016-06-05
军营文化天地(2016年3期)2016-05-25
中国学术期刊文摘(2016年2期)2016-02-13
新乡学院学报(2015年6期)2015-11-06
湖南城市学院学报(自然科学版)(2015年3期)2015-08-24
电力工程技术(2014年5期)2014-03-20

