电偶极子切分算法研究

胡瑞华，林 君，孙彩堂, 刘长胜, 周逢道

(吉林大学 仪器科学与电气工程学院, 长春 130061)

0 引言

当前电磁法勘探已成为解决地质问题的重要手段[1-2]，学者们通过正反演理论和技术来研究地质模型的电磁响应和地下结构的复现，考虑到探测系统的发射功率和分辩能力，野外作业时常采用人工源激发达到获取高信噪比的电磁数据的要求。磁性源和电性源是常被采用的两种人工源，其中电性源使用一定长度的导线向地下供一定强度的交变电流来实现。在以电性源为场源的电磁探测方法中，其正演常需要研究基于电偶极子激发的场响应，并根据响应规律来解释野外实测数据(即反演)[3～12]。这种正反演通常都是假定发射端与接收点距离远大于供电两端的长度，即要求导线长度满足偶极子的条件。文献[4]指出，当收发距大于等于10倍的导线长度时，导线可被看作是电偶极子。然而在实际应用中由于受地形地貌、发射功率等多种因素的制约，导致长导线并不满足电偶极子的条件，而使基于电偶极子的场计算公式不再适用，在这种情况下若仍然按照电偶极子激励理论开展数据解释，将造成较大偏差甚至是错误的地质结构的复现。为了解决这个问题，在正反演中可以先将长导线源切分成若干个电偶极子，然后对切分的电偶极子的响应进行求和，以达到计算长导线源场响应的目的。

针对如何将长导线源切分成多个电偶极子的方法，本次研究并实现了两种切分算法，①借鉴二分法思想设计的递归切分算法；②是借鉴穷举法思想设计的穷举切分算法。通过对两种切分算法的研究表明：递归切分算法切分出的电偶极子数目相对较多；穷举切分算法在穷举步长较小(如0.1 m)时能较准确地切分出真实电偶极子的位置。将两种算法应用有于CSAMT电场的计算中，计算结果表明：两种切分算法都可应用于实际场的计算。

1 切分算法原理

1.1 观测点与长导线源的拓扑结构

人工源野外测量时，观测点离长导线源有一定的距离，接收和发射之间的是三维拓扑结构[9,11]，常见的拓扑结构有平地形的地面发射地面接收、起伏地形的地面发射地面接收、地面发射井中接收等(图1)。

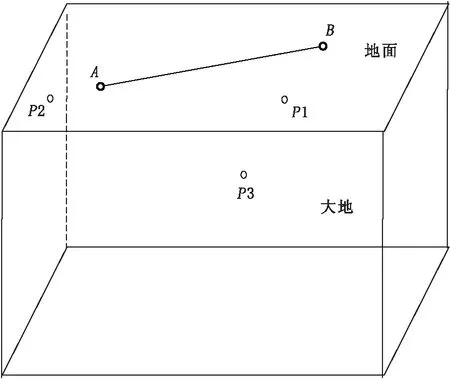
图1 观测点与长导线源的拓扑结构Fig．1 Topology structure of survey point and long lead source

图1中长方体代表大地，AB表示长度为AB的长导线发射源，A和B分别代表发射源的两极，P1、P2、P3分别表示与AB共面、共线和地下的观测点。P1、P2、P3与AB的三种位置关系与野外测量时的施工布局一致。偶极子的位置常用发射源两极(导线两端)的中点代表。若空间坐标系中A极、B极、测点P三点坐标分别取为A(xA，yA，zA)、B(xB，yB，zB)、P(xP，yP，zP)，其中x、y、z表示点的坐标分量，若用C表示AB的中点，则接收点与发射源的距离(发收距)表示为P点到C点的距离PC(常用r字符表示)。根据A、B坐标及代数关系很容易计算出C点的坐标、发收距PC和发射极距AB。另外，偶极子的条件是收发距大于等于N(通常最小值可取为10)倍的导线长度，即PC≥N*AB。实际应用中A、B、P三点坐标已知，而N参数的确定可在综合考虑工区、收发系统参数以及电磁数据质量的情况下选定。

1.2 二分法递归切分算法

二分法算法是一种快速搜寻算法，算法的核心是从有序数据列中按照折半查找的方式寻找满足条件的结果[12-14]。借鉴二分法思想研究切分长导线源为多个电偶极子的算法如下：

1) 根据长导线两端A点、B点的坐标计算其中点C的坐标和A点到B点的距离AB；根据P点、C点的坐标计算P点到C点的距离PC，转到步骤2)。

2) 如果PC≥N*AB则记录下C点的位置，算法结束；否则转到步骤3)。

3)用C点坐标替换B点的坐标，转到步骤1)。

4)用C点坐标替换A点的坐标，转到步骤1)。

此算法是递归算法，共分四步。第一步计算发射距AB和收发距PC，为算法的下一步作准备；第二步判断AB是否为电偶极子，若是电偶极子，则AB的中点就是电偶极子的位置，算法结束，它是递归算法的出口；第三步当AB不是电偶极子时，搜寻CA段导线电偶极子的位置；第四步当搜寻完CA段导线的电偶极子时，再搜寻CB段导线的电偶极子。每递归一次就能找到一个电偶极子，当整个递归算法结束时，便找到了所有电偶极子的位置点(图2)。

图2 二分法递归切分算法流程图Fig．2 Flow of binary segmentation method

1.3 穷举切分算法

穷举算法是一种试算遍历算法，算法的核心是从取值区间对每个取到的值(或组合值)进行试算，通过判断试算结果是否满足要求，从而找到问题的解[12,15]，这种算法常被用在方程少而未知数多的问题中。将长导线源切分为多个电偶极子的问题，本质上是查找AB上哪些点是偶极子的位置，但我们仅知道偶极子的条件PCnew≥N*AnewBnew(式中AnewBnew表示AB上的一段导线，Cnew为其中点)，这样必须通过1个方程(PCnew=N*AnewBnew)求解AnewBnew的中点Cnew的位置(即要确定Cnew的3个坐标分量)，显然方程少而未知数多，无法直接求解出方程的解，即无法定位偶极子的位置，因此这个问题属于穷举算法能解决的范畴。借鉴穷举算法的思想，设计将长导线源切分为多个电偶极子的算法如下：

1)根据切分步长以A或B为参考点(算法描述中以A为参考点)对AB进行切分，得到切分点列表C=(C1,C2,…，Cn);设置两个计数器变量i、j，并使i= 0，j= 0，转到步骤2)。

2)改变i使i=i+1；计算点P到点Ci的距离PCi，点Ci到点B的距离CiB，点Ci到点A的距离CiA，转到步骤3)。

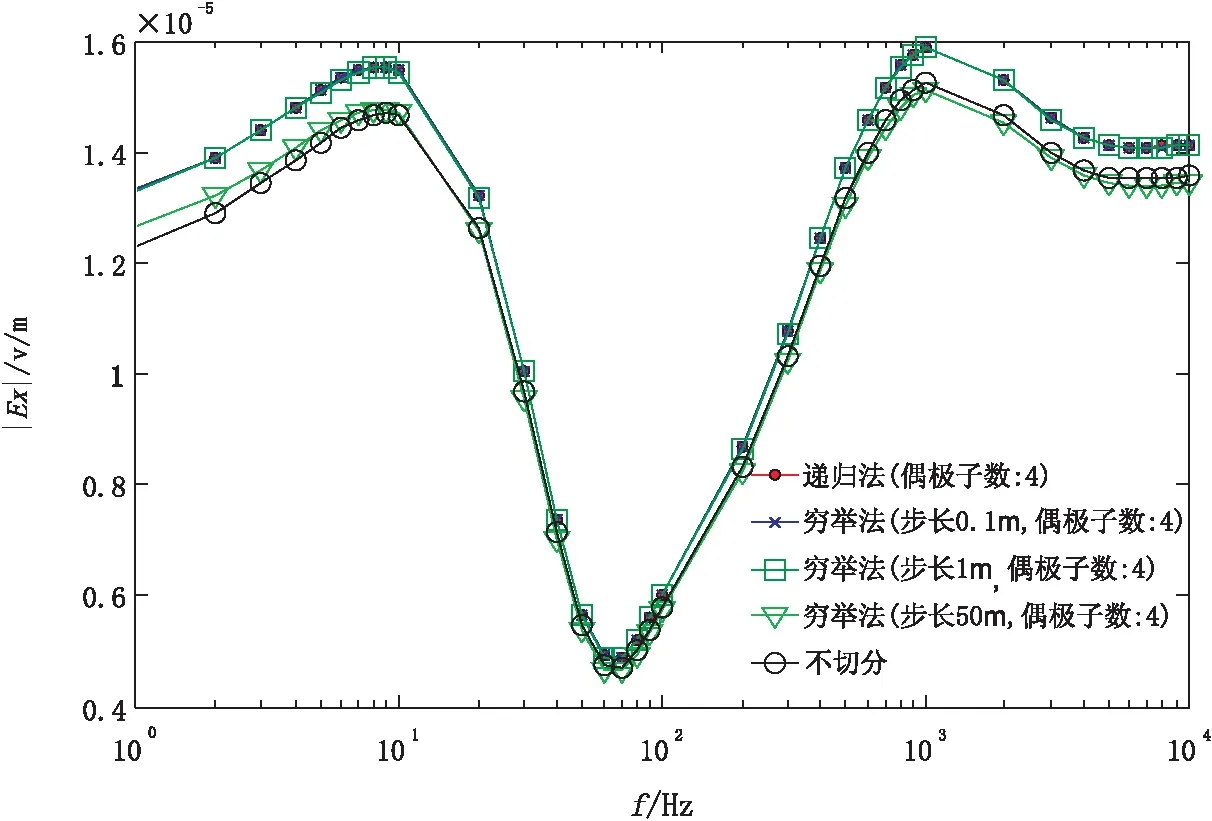
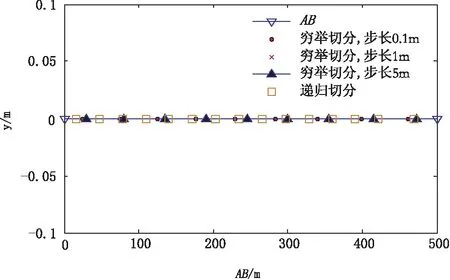
3)如果PCi

4)改变i使i=i-1，如果CiB≥CiA，则记录下Ci；用Ci+j的坐标替换A点的坐标；i=i+j，j=0，转到步骤6)；否则转到步骤5)。

5)记录下AB的中点，结束算法。

6)改变j使j=j+1，转到步骤2)。

算法共由六步组成。第一步是参考穷举算法的原理根据切分步长对AB长导线源进行切分，切分的小段中除最后一小段外，其他的切分小段长度是等长的(若AB能被步长整除，则所有切分出的小段长度都是等长的)，并记下所有的切分点Ci，偶极子的位置就存在于这些切分点中和最后一个偶极子的中点，为了能找到偶极子的位置，用i变量跟踪切分点的位置，用j变量跟踪上一个偶极子B端到Ci的切分点个数；第二步计算PCi、CiB、CiA；第三步和第四步判断PCi是否同时满足偶极子的条件和CiB是否为原AB的最后一段，在两个条件都满足情况下，则记下Ci，然后计算出下一个待求偶极的A端位置，然后执行第六步进入查找下一次偶极子的循环中；另外，在第四步中若CiB是原AB切分段的最后一段，则偶极子的位置直接取CiB的中点，算法结束(图3)。

图3 穷举切分算法流程图Fig．3 Flow of exhaustion segmentation method

2 算法应用

使用两种算法对地表长导线源AB，其中A极坐标为(0，0，0)，B极坐标为(500，0，0)，观测点P坐标为(50，500，0)进行偶极子的切分，偶极子的条件取为收发距是10倍的发射距。切分的偶极子位置对比如图4所示。

图4 两种算法切分结果对比Fig．4 Segmentation results comparison to two algorithms

穷举切分算法切分步长分别选择0.1 m、1 m和5 m，用这三种步长切分的偶极子数目都是9个。从图4可以看出，用步长0.1 m和步长1 m切分出的偶极子位置差别很小，与理论上的准确偶极子位置基本一致；而用步长5m切分出的偶极子位置与用步长0.1 m切分出的偶极子位置差别明显。如果将0.1 m步长切分出的偶极子看作是真实(理论上)的偶极子，那么切分步长越大切分出的偶极子的位置与真实偶极子的位置误差就越大。采用递归算法切分出的偶极子数目为15个，多于0.1 m步长的穷举法切分的偶极子数目，表明递归算法切分的偶极子长度要小于用穷举法切分的偶极子的长度。

为了进一步了解场计算中需要将长导线源切分为多个电偶源的必要性及算法的有效性，本次研究以可控源音频大在电磁法(CSAMT)一维电场计算为例对其说明。与切分算法相关的参数：发射源极距AB长 2 000 m，A点坐标为(0，0，0)，B点坐标为(2 000，0，0)，观测点P位于离AB垂直距离 7 000 m 处，坐标为(0，7 000，0)，偶极子的条件取收发距是10 倍的发射距。使用文献[1]中场的计算公式求解一个三层H型地电模型(电阻率：300 Ω·m，50 Ω·m，1 000 Ω·m；厚度：300 m，200 m)x方向的电场，并分别使用文中的两种切分算法和不切分三种方式计算出的电场结果如图5所示。

图5是频率-电场曲线图，从图5中可以看出，用两种算法切分的偶极子数目都为 4 个，且用递归算法切分的偶极子计算出的电场曲线与用穷举算法在步长分别取 0.1 m、1 m 切分的偶极子计算出的电场曲线基本重合，这表明了递归切分算法可用于实际应用中；而步长取 50 m 切分的偶极子计算出的电场曲线与步长取 0.1 m 切分的偶极子计算出的电场曲线明显分离，表明用较大步长切分偶极子计算出的电场会带来较大的误差；不做任何切分计算得到的场曲线与用0.1 m步长切分后计算得到的场曲线不重合，这表明在不满足偶子条件的情况下，若仍然按照偶极子激发公式计算场将会得到不正确的结果。

3 结论

采用长导线源激励时，为了避免收发距较小时源长度对场计算的影响，需要考虑到将长导线源切分为多个偶极子源，这样长导线源场的计算就转化为多个偶极子场的叠加。递归切分算法和穷举切分算法都可以实现对长导线的切分。在实际物探应用中，递归切分算法可直接使用，穷举算法的切分步可取 0.1 m或 1 m。

图5 两种切分算法和不切分电场计算结果对比Fig．5 Electric field calculating comparison to two segmentation algorithms and no segmentation

参考文献：

[1] 汤井田, 何继善.可控源音频大地电磁法及其应用[M]．长沙: 中南大学出版社,2005．

[2] 何继善．可控源音频大地电磁法[M]．长沙:中南大学出版社,1990.

[3] 王刚,王书民, 雷达，等.CSAMT场源效应试验研究[J].物探化探计算技术,2011,33(5):527-530.

[4] 赵广茂,李志华,朱旭东，等.长导线源CSAMT一维正演研究[J].铁道工程学报,2010,143(8):21-24.

[5] 殷长春. 可控源音频磁大地电流法一维正演及精度评价[J].长春地质学院学报,1994( 4):438- 453.

[6] 孙娅,何展翔,柳建新，等. 长导线源频率域电磁测深场源静态位移的模拟研究[J].石油地球物理勘探,2011,46( 1):149-154.

[7] 李勇,林品荣,徐宝利.电离层影响层状介质长导线源的电磁场[J].物探化探计算技术,2009,31( 3):183-188.

[8] 刘昱,李云哲,黄子莹.水平长导线源瞬变电磁三维积分方程模拟[J].现代地质,2010,24(2):397-402.

[9] 屈有恒,张贵宾,晋风明.倾斜线源的三维电场数值模拟研究[J].物探化探计算技术,2007,29(5):431-435.

[10] 许振奎,张胜业.层状介质中磁性源频率测深的一种视电阻率算法[J].勘探地球物理进展,2004,27(5):333-336.

[11] 徐建华,朱德怀,胡文宝，等.多层介质中偶极子场的系数递推关系[J].石油地球物理勘探,1994,29(1):69-74.

[12] ALSUWAIYEL M H. Algorithms Design Techniques and Analysis[M].Beijing: Publishing House of Electronics Industry,2003.

[13] 王海涛,朱洪.改进的二分法查找[J].计算机工程,2006,32(10):60-62.

[14] 陈宝平.递归算法的设计模式与调试[J].电子科技,2011,24(9):28-33.

[15] 孙义欣,冯娜.穷举法在程序设计中的应用[J].计算机时代,2012,8:50-52.