范氏气体准静态开放式系统与气枪子波模拟
张雪阳,袁修贵*,朱世华,赵庆献,伍忠良
(1.中南大学 数学与统计学院,长沙 410083;2.广州海洋地质调查局,广州 510760)
0 引言
现阶段,海上地震勘探一般使用气枪或气枪阵列激发地震波,在生产中由于人力物力的限制,实际操作十分困难。因此对气枪震源子波激发原理进行深入研究,通过计算机对气枪激发子波和气泡在水中的振荡过程进行数值模拟,并对气枪压力、气枪容量、沉放深度等影响因素进行分析就变得十分必要。
在气枪震源子波模拟的研究中,国外已给出多种基于“自由气泡振荡理论” 的模型,其中代表性的有Ziolkowski[1]模型、Safar[2]模型、Schulze-Gattermann[3]模型等。陈浩林[4]在Ziolkowski模型基础上,将气枪压力和气枪容积进行了修正,使模拟子波与实验数据更加接近。然而这些模型都没有考虑气枪枪口的节流、气泡壁的热传导等作用对模拟结果的影响。Landrø[5]根据准静态开放式热力学系统的热力学第一定律得到
hdm+dQ=dU+PdV
(1)
其中h是摩尔焓;m为气体摩尔量;Q为系统吸放热能;U为内能;P为压强;V为体积。并利用Kirkwood-Bethe[6]的阻尼气泡运动方程,建立了理想气体的单枪子波模型。王立明[7]在Landrø的准静态开放式热力学系统基础上,利用范德瓦尔斯气体理论,建立了范氏气体子波模型,使模拟结果比理想气体模型跟接近实验数据。
在王立明等[8]的子波模拟过程中的准静态开放式系统方程均直接引用了Landrø的准静态开放系统方程(1),其中理想气体条件下焓h=CpT(Cp为定压摩尔热容);而在范氏气体条件下焓h≠CpT,显然直接使用焓h=CpT得到的准静态开放式热力学系统方程

(2)
是不合理的。
本次研究将对比理想气体准静态开放式系统方程的推导过程,给出在范氏气体条件下的准静态开放式热力学系统方程的推到过程及结果,并利用四阶Runge-Kutta方法对范氏气体模型进行模拟分析。
1 理想气体下的准静态开放系统
摩尔焓的计算公式可由公式(3)给出
h=U+PV
(3)
在理想气体条件下,每摩尔理想气体的内能为
U=CvT
(4)
其中Cv为等体积摩尔热容。
由理想气体状态方程
pV=RgT
(5)
得到
h=CvT+RgT=(Cv+Rg)T=CpT
(6)
其中 理想气体状态下Cp=Cv+Rg;Cp为等压摩尔热容;Rg为普适气体常量。
由理想气体的内能公式
U=mCvT
(7)
得理想内能变化率:
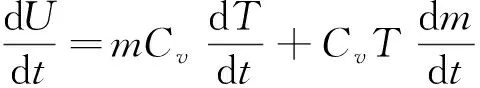
(8)
将式(7)、式(8)带入式(1)化简可得:

(9)
方程(9)即为理想气体准静态开放系统方程。
2 范氏气体下的准静态开放系统
每摩尔范氏气体的内能为:
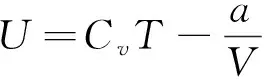
(10)
由范氏气体状态方程

(11)
得到

(12)
将式(10)、式(12)带入式(3),可得:
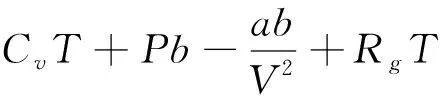
(13)
由范氏气体内能公式

(14)
得内能变化率


(15)
将式(13)、式(15)带入式(1)化简可得
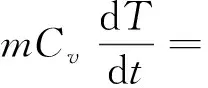
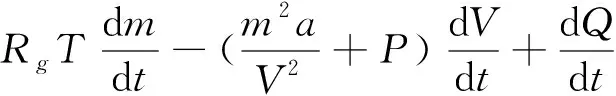
(16)
方程(16)为范氏气体条件下的准静态开放式系统方程。
与现有文献使用的范氏气体条件下的准静态开放式系统方程[7-8]
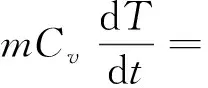
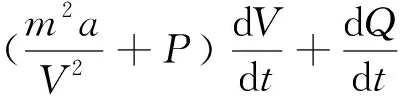
(17)
是有差别的。
3 范氏气体子波模型数值模拟
对范氏气体进行子波模拟,还需要气泡振荡方程和其他一些参量,其中采用Gilmore[9]的气泡振荡方程为

(18)
其中R为气泡半径;R′,R″分别为气泡半径R对时间的一阶导数和二阶导数;H为气泡壁处瞬时焓差;H′为焓差H的一阶导数;c为声波速度。
气泡内气体与周围水热转换率为:
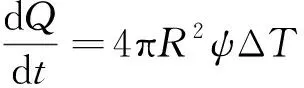
(19)
其中 传热系数ψ可通过子波模型实验来确定;温度差ΔT=T-Tw;T为气泡内温度;Tw为周围水的温度。
气体转移率有如下经验公式:
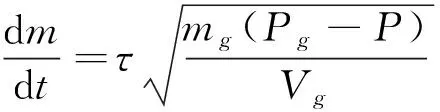
(20)
其中τ为气体节流系数,可以表示为
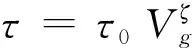
(21)
式中τ0为独立于气枪容积的气体节流常数;ζ为气体节流幂指数。
考虑气泡近似球体,其体积与气泡半径的关系式为:
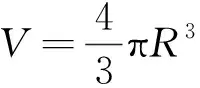
(22)
由式(22)求导可得体积变换率为:
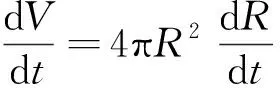
(23)
在实际气枪激发过程中,气枪内气体没有完全充入气泡内部,气枪关闭后仍有一部分气体留在气枪气室内部,用η来表示气枪内剩余气体摩尔量与初始气枪内气体总摩尔量的比值
(24)


(25)
式中 常量Pc=139 MPa。
气泡内气体初始摩尔量m|t=0和气枪内气体初始摩尔量mg|t=0,可通过范德瓦尔斯方程(26)求得。
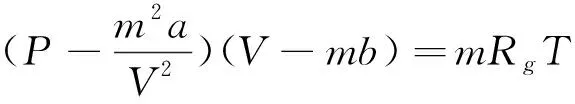
(26)
范氏气体模型可以通过四阶Runge-Kutta方法求解。算法步骤如下:

2)k时刻,气泡内压强P|t=k可通过范德瓦尔斯方程求得。
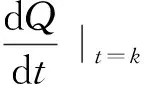


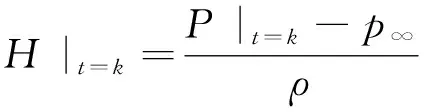
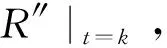
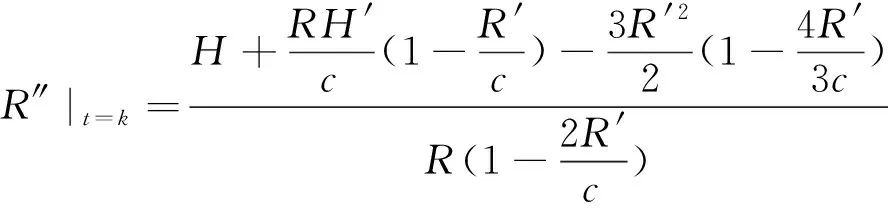
8)计算k时刻压力子波p|t=k:

10)k:=k+1,转到步骤2),最终得到整个震源子波压力场。
4 模拟结果分析
在实验中,我们选用Sleeve I型气枪进行模拟,气枪震源沉放深度为6 m,气枪工作压力为2 000 psi,气枪容量为40 in3,海水温度为18℃。图1~图3分别表示在同样条件下的实测子波,王立明[7]、李高林[8]等模拟的原范氏气体子波模型和本文所给出的范氏气体子波模型。

图1 气枪实测远场子波Fig.1 Measured far-field air gun signature
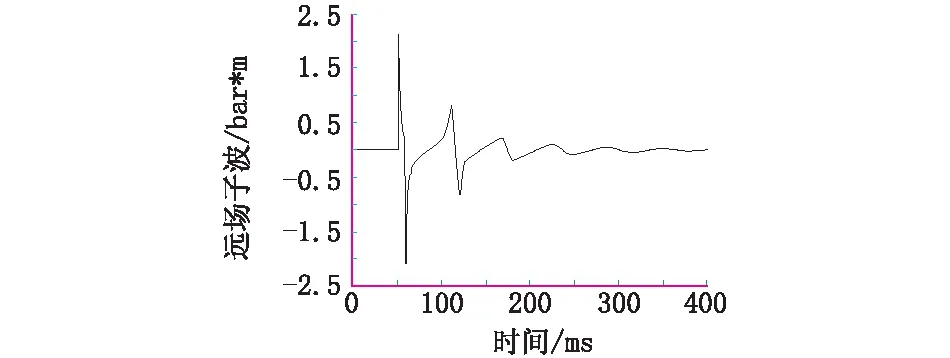
图2 原范氏气体子波模型模拟结果Fig.2 Results of simulation by the old Van der waals gas mode
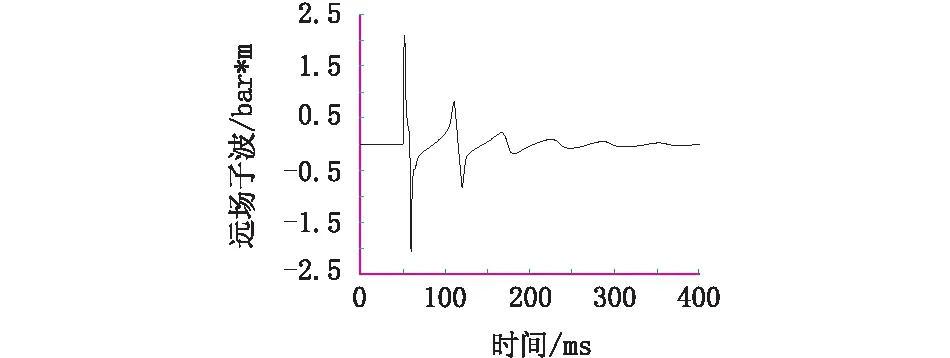
图3 范氏气体子波模型模拟结果Fig.3 Results of simulation by the Van der waals gas mode
对图1、图2及图3子波参数通过表1进行比较分析。
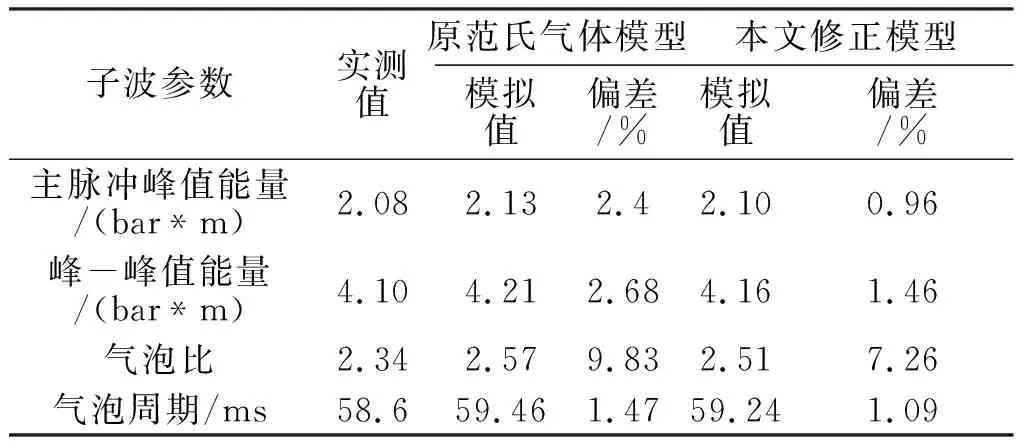
表1 实测子波与范氏气体模型子波参数对比
通过表1的对比分析结果发现,本文的范氏模型参数比原范氏气体模型参数更接近实测数据,模拟子波与实测子波基本一致。说明本文推导的范氏气体条件下的准静态开放式热力学系统与实际情况更加接近,能更准确地表现子波属性。
5 结束语
本次研究在Landrø准静态开放式热力学系统的基础上,论证了在范氏气体条件下,不能简单使用理想气体下的准静态开放式热力学系统方程;给出了范氏气体条件下准静态开放式热力学方程的推导过程及结果;并利用推导结果结合实际数据进行了计算机数值模拟分析。数据分析表明,模拟子波和实验子波吻合很好,得到了更加准确的子波模拟结果。
参考文献:
[1] ZIOLKOWSKI A. A method for calculating the output pressure waveform from an air gun [J]. Geophysical Journal of the Royal Astronomical Society, 1970, 21(2): 137-161.
[2] SAFAR M H. The radiation of acoustic waves from an air-gun[J]. Geophysical Prospecting, 1976, 24(4): 756-772.
[3] SCHULZE-GATTERMANN R. Physical aspects of the "airpulser" as a seismic energy source[J]. Geophysical Prospecting, 1972, 20(1): 155-192.
[4] 陈浩林, 於国平. 气枪震源单枪子波计算机模拟[J]. 物探装备, 2002, 12(4): 241-244.
[5] LANDRØ M, SOLLIE R. Source signature determination by inversion[J]. Geophysics, 1992, 57(12): 1633-1640.
[6] KIRKWOOD J. G, BETHE H. Progress report on "The pressure wave produced by an underwater explosion I"[R]. Office of Scientific Research and Development Report , 1942.
[7] 王立明. 范氏气体下气枪激发子波信号模拟研究[D].西安: 长安大学, 2010.
[8] 李高林. 气枪震源子波特性分析与处理技术研究[D]. 青岛:中国海洋大学, 2011.
[9] GILMORE F R. Collapse of a spherical bubble. Report Hydrodynamics Laboratory[M]. California Institute of Technology, Pasadena, California, 1952.

