麦克斯韦速率分布函数的教学探讨

曹剑英 葛俊峰 彭先华

(集宁师范学院物理系 内蒙古 乌兰察布 012000) (扬州高等职业技术学校 江苏 扬州 225000)

麦克斯韦气体分子速率分布律是普通物理学热学部分中一个讲授和学习的重点和难点，然而现行教材中都是直接就给出结果，没有任何推导过程，对大多初学者来说是充满好奇而又不能够自然地接受.通过运用统计规律作出详细地理论推导，为广大师生作教学参考.

在1859年麦克斯韦用概率统计的理论建立了一个分子速率分布函数的形式,也称速率分布律

其中k为玻尔兹曼常量，m和T分别为气体分子量和温度.

1 分子速率分布的实验测定

由于分子速率分布律是从概率理论推导出来的，人们自然很关心它的实际可靠性，试图通过实验来验证.

因受技术条件的限制，气体分子速率分布的实验，直到20世纪20年代才得以实现.图1是实验所用装置.

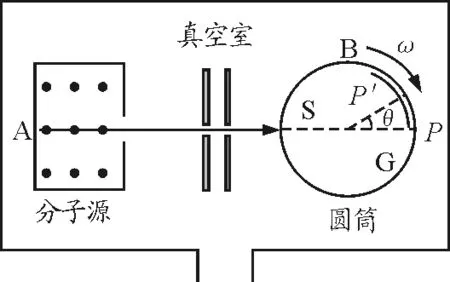
图1 测定分子速率分布的实验装置

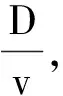
或

上式表明，弯曲板上不同弧长l处沉积的分子具有不同的速率.测量沉积的分子层厚度，即可求得分子束中各种速率v附近的分子数占总分子数的比率，从而得出分子速率的分布律[1].

2 麦克斯韦速率分布函数

设容器内有一定量的处于热平衡态的气体，气体分子总数为N，分子速度在三维空间的分量为vx，vy，vz.在速率区间vx～vx+dvx，vy～vy+dvy，vz～vz+dvz内分子数dN与总分子数N和速率体积元dvxdvydvz的乘积成正比，即

dN=NF(v2)dvxdvydvz

上式表示单位速率间隔内的分子数占总分子数的百分比.根据统计假设，对某一给定的速率，分子在各个方向运动的概率是相等的.各速率分量相互独立，因此

令

F(v2)=f(vx)f(vy)f(vz)

(1)

假设

积分后得

令常量A1=A2=A3=A，代入式(1)得

若考虑到无限大速率分子出现的概率极小，λ必为负值，令λ=-α2，由速率分布具有归一化条件得

将

代入上式得

于是

(2)

在温度为T时，由能量均分定理，单原子分子的平均平动动能为

由

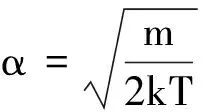
(3)

若单原子气体分子速率分布函数，用球坐标描述方程，dvxdvydvz→v2dvdΩ(其中dΩ为立体角).所以气体分子速率在v～v+dv区间的分布可表示为

(4)

将式(3)代入式(5)即可得出麦克斯韦速率分布律

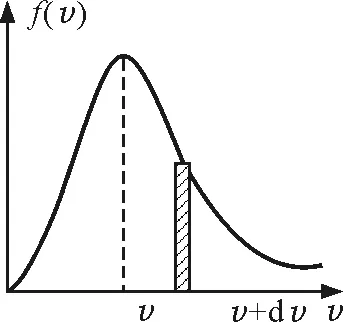
图2 麦克斯韦速率分布曲线

3 从速率分布函数f(v)推算分子速率的三个统计值

在分子动理论中，常用到以下三种速率.

3.1 最概然速率(最可几速率)vp

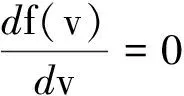
因

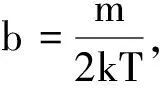
所以

3.2 平均速率

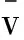
对于连续分布，上式有

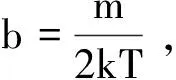
将b值代入

3.3 方均根速率

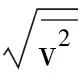
及

将麦克斯韦速率分布函数f(v)代入，可得理想气体分子的方均根速率为

压强公式推导出结果是一样的[2].

4 总结

麦克斯韦速率分布律是一条很重要的物理定律，在内容和方法上都与以往有较大的不同，是学生从学习力学、热学以来所遇到的一种崭新的研究方法，初学者既感到新鲜，又感到繁难.此知识点采用什么方法讲授是广大同行关注的问题.

笔者应用统计规律对麦克斯韦速率分布函数进行合理、严密的数学推导，对课堂上没有充足时间推导的教师们给出一些参考，同时也对学生在自主学习的过程中起到了桥梁的作用.

参考文献

1 赵近芳.大学物理简明教程.北京：北京邮电大学出版社，2008

2 陈秉岩，等.麦克斯韦速率分布律的推导方式探讨.河海大学常州分校学报，2006(6):15～21

3 程守洙.普通物理学(第五版).北京：高等教育出版社，2006