主成分分析在航空瞬变电磁去噪中的应用

武 莹， 陆从德， 杜兴忠， 余小东

(1. 成都理工大学 信息科学与技术学院，成都 610059；2. 成都理工大学 地球物理学院，成都 610059；3.中国水电顾问集团 贵阳勘测设计研究院，贵阳 550081)

0 前言

航空瞬变电磁法是一种快速地球物理勘查方法，因其勘探效率高，成本相对较低，可大面积勘探等优势，而广泛用于地质填图、矿产资源勘查、油气勘查，以及水文、工程、环境监测等各个领域[1]。为了避免激发源的影响，航空瞬变电磁法常常对二次场数据进行处理和解释，以获得地下介质分布信息。关于航空瞬变电磁二次场信号：①由于该信号是一种宽频带信号，因此易受到多种噪声的影响，例如随机噪声、天电噪声和人文噪声等；②由于二次场信号能量较弱，导致中晚期的信号被噪声严重污染，使得处理和解释结果不可靠或者不可信。为了解决上述问题，设计出保幅去噪方法就显得尤为重要[2-3]。

关于航空瞬变电磁去噪研究，已经有许多学者提出了不同的去噪方法，①最小二乘滤波和频率域的线性滤波法可以减弱随机噪声的影响[4-5]，但是前者在有效信号和噪声相关时不能获得较好的效果，而后者往往存在吉布斯现象，即所谓的边缘效应；②裁剪法、中值滤波法、小波阈值滤波法可以有效地抑制天电噪声[6-9]，但是裁剪法主要针对叠前数据，中值滤波在抑制具有不同时宽的天电噪声时性能较差(这是因为所取窗口的大小形状会对滤波效果造成较大影响)，小波阈值去噪法对于幅值变化不大的信号有很好的效果，但是对于幅值变化较大的航空瞬变电磁信号不能获得较佳的去噪性能；③锥形叠加法以及局部噪声预测滤波法、自适应滤波方法等基于预测或递归滤波的去噪算法，对于抑制航空瞬变电磁数据中的人文噪声有很好的效果[6,10-12]，但是锥形叠加法主要用于叠前数据，预测滤波算法要求很多的输入参数，其实现较为复杂，很难应用于工程实践，自适应滤波方法具有普适性，但是其去噪效果有待改进。在实际的航空瞬变电磁勘查中，影响有效信号的噪声种类很多，往往是复杂的和不可预测的，而上述各种方法都只能处理单一噪声，不能同时抑制天电噪声和人文噪声。从目前有关研究文献可知，天电噪声和人文噪声是航空瞬变电磁噪声的主要来源[3]，为此寻找一种计算简单又同时可以抑制航空瞬变电磁主要噪声的去噪方法，就成为了提高处理和解释精度的关键内容之一。

主成分分析法(PCA)能对含噪信号分析，达到信噪分离的目的。目前已有研究者应用PCA法到地球物理数据处理中。夏江海[13]在位场资料处理中应用奇异值分解有效抑制了随机噪声；王权海等[14]将PCA方法应用于地震数据处理中，极大提高了地震数据的信噪比；Reninger等[15]把奇异值分解作为一种去噪工具,应用到航空瞬变电磁数据处理中。在文献[ 15]中，尽管奇异值分解法对天电噪声和人文噪声具有良好的去噪效果，但是其在确定信噪分离准则时需要较为复杂的条件(例如飞行高度和飞行视频等)，不易应用到工程实践中。作者同样使用主成分分析方法对航空瞬变电磁数据进行分析，但是在确定信噪分离准则时使用较为简单的L曲线法，不仅能获得良好的去噪效果，而且易于嵌入到航空瞬变电磁处理与解释软件中，应用于工程实践。

1 基于主成分分析的航空瞬变电磁去噪方法

对于航空瞬变电磁数据来讲，由于地下电性特征具有一定的分布规律，所以观测到的电磁场数据随空间、时间、频率、极距和发收距的变化也遵循一定规律，这种规律性在数学上就是线性相关性。可以认为反映地下电性特征的数据是由数据矩阵中各列间相关性很高的部分组成，而数据中不相关的部分则认为是各种噪声和干扰[16]。这就是说，能量较大的主要成分代表地下电性特征，能量较小的成分代表了各种噪声和干扰。实际上这也是在航空瞬变电磁去噪中应用主成分分析法的依据。

设XXm×n表示航空瞬变电磁二次场，其中n表示测点，m表示时间道，于是获得基于主成分分析的航空瞬变电磁去噪方法的计算步骤为：

(1)对XXm×n进行归一化获得Xm×n。

(2)计算Xm×n的协方差矩阵Dm×m。

(3)对协方差矩阵Dm×m进行特征值分解，即D·V=Λ·V。其中，Λ是特征值矩阵，Λ=diag(λ1,λ2,…,λm)，且λ1≥λ2≥…≥λm≥0；V是m×m的特征向量矩阵，且VVT=I。

(4)计算X在V中的投影，即Y=VTX，得到矩阵X的主成分y1、y2、…、ym。

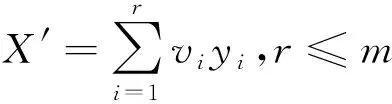
2 L曲线法

L曲线法最先由Lawson等[17]提出，然后被Hansen[18]用来确定正则化法的参数，以便求解病态问题。该方法认为：把残差项作为横坐标，正则化项作为纵坐标，然后通过L曲线的角点即可确定所要求的正则化参数。所获得的曲线具有L-形状，所以命名为L曲线法。实际上早在1989年Hansen[19]就已经证明了Tikhonov正则化方法和奇异值分解(包括广义奇异值分解)的关系，并认为正则化参数控制了正则化项和残差项的加权，而这些权值相当于奇异值分解中的特征值，描述了其对各个特征分量的贡献。在应用PCA对信号进行分析时，特征值表征了其相应的特征向量(或称为成分)对信号的贡献程度，因此可以引入L曲线法作为信噪分离准则。在基于L曲线的信噪分离准则中，对特征值进行降序排列，以特征值索引作为横坐标，特征值作为纵坐标，那么所获得的特征值曲线可以近似为L曲线。对于完全满足L形状的曲线，要确定其角点是比较容易的，但是对于不满足L形状的曲线，要确定其角点就比较困难。对于后一种情况，作者采用的方法是：首先求解相邻两个特征值的斜率，然后求前一斜率和后一斜率的比值，具有最大比值所对应的特征点就是所要求的L曲线的角点。也就是说，从特征值的斜率曲线来看，具有最大突变的特征值就是信噪分离的基准点。当然，再结合衰减曲线趋势对比法，可以获得更为合理的结果。

3 实验结果及分析

为了验证主成分分析方法在航空瞬变电磁去噪中的正确性，首先对正演模拟响应曲线进行主成分分析，确定有效信号的分离准则；然后使用实测数据进一步检验该方法的有效性和适用性。

3.1 模拟数据实验

3.1.1 模拟数据的产生及主成分分析结果

MAXWELL软件是一款由澳大利亚EMIT公司开发、基于Windows操作系统平台的电磁正反演和处理软件。本文的模拟数据由MAXWELL软件中的有限元法正演得到，地电模型为层状介质。首先正演产生了15 s的模拟数据，同时也产生模拟的随机噪声和天电噪声，然后通过五个周期叠加和抽道，分别获得了75个测点的模拟数据和含噪数据，且每个测点的时间道数为20个。图1(a)给出了单测点的模拟衰减曲线，图1(b)所示为含噪的模拟衰减曲线。

根据上述的计算步骤，对图1(b)所示的含噪电磁数据进行主成分分析，获得20个成分如图2所示。

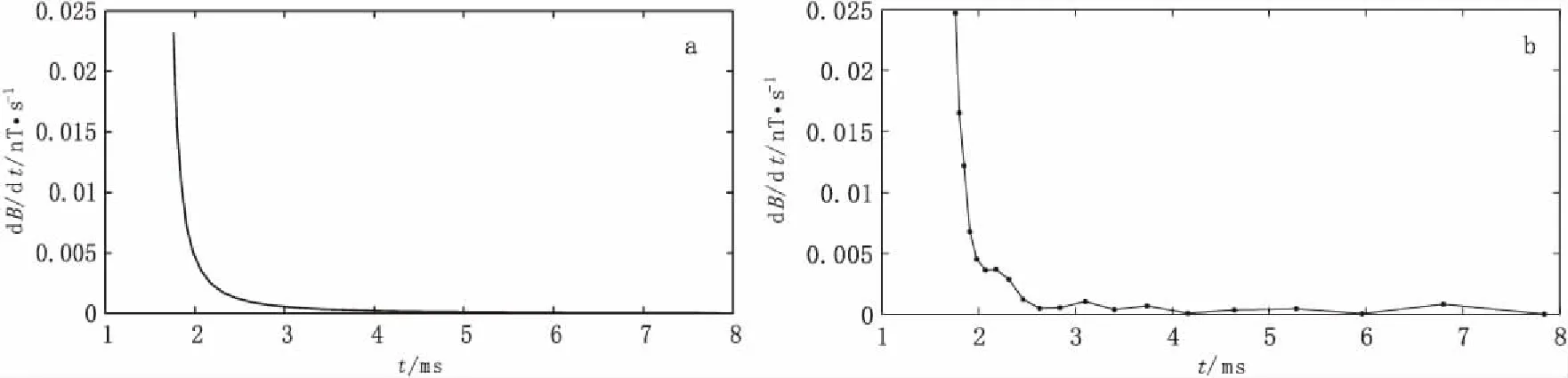
图1 模拟电磁响应衰减曲线Fig．1 The attenuation curves of EM response simulated(a)模拟响应曲线； (b) 含噪的模拟响应曲线

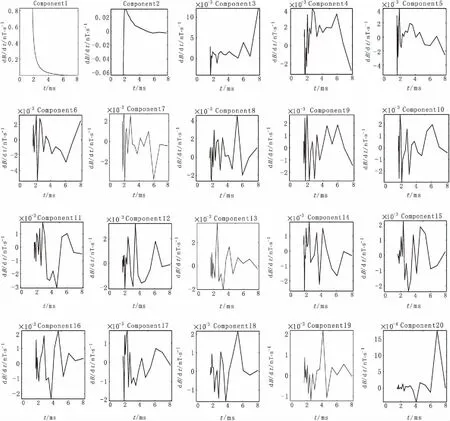
图2 20个互不相关的成分Fig．2 Plots of 20 uncorrelated components

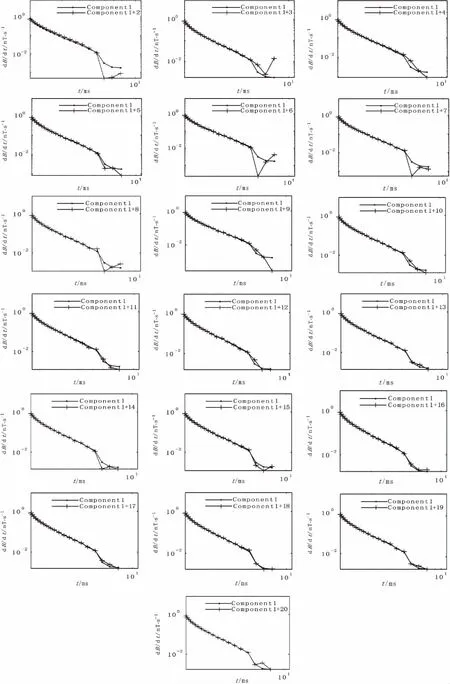
图3 成分趋势对比Fig．3 Contrastive plots of component trend

从图2中可以看出，响应曲线经主成分分析后，把原始数据分解为20个互不相关的成分，而且每一个成分都是按照特征值的降序排列的。第一个成分比其他的成分都光滑，更接近原始的衰减曲线；随着特征值的减小，所对应的成分出现了不同程度的波动，说明在这些成分中存在很强的噪声。

尽管从图2中可以看到随着特征值的减小，数据各个成分的变化趋势，但不能明确地判别出反映地下信息的有效成分。为了能合理获得反映地下介质分布的有效成分，本文使用曲线趋势对比法和L曲线法对分解后的成分进行分析，从而分离出分别代表有效信号和噪声的成分。

3.1.2 基于曲线趋势对比的信噪分离准则

首先用表示衰减曲线趋势的第一主成分与其他的各个成分合并，然后与衰减曲线的主要趋势(第一主成分)作对比[15]，如图3所示。

第一主成分代表衰减曲线的主要趋势，因此其反映了地下介质分布的主要信息。现在主要判断其他成分到底反映的是地下介质信息还是噪声？为此，分别合并第一主成分和其他成分，如果某成分代表有效信号，那么该成分和第一主成分合并后所获得的曲线趋势不同于第一主成分；如果某成分代表噪声，那么合并后的曲线趋同于第一主成分，但是其中会有个别点发生跳动，这是因为噪声不可能改变整个曲线趋势，而只是影响曲线的局部形状。

利用上述的信噪分离准则分析图3，可以看出，成分1分别与成分2、成分3合并后的整体曲线变化趋势不同于成分1，而成分4-成分20分别与成分1合并后的曲线除了在个别点有不同程度的跳变外，整体的趋势基本与成分1一致，所以认为成分1、成分2、成分3 是有效地质成分，成分4-成分20 是噪声成分。

3.1.3 基于L曲线的信噪分离准则

尽管基于曲线趋势对比法可以区分地质成分和噪声成分，但是它主要是依靠人来判断，因此具有一定的主观性。为了更为客观地、定量地判别地质成分和噪声成分，这里给出了基于L曲线的信噪分离准则。同时，该准则也可以和曲线趋势对比法进行相互验证。

图4(a)为含噪的模拟电磁响应数据的L曲线(归一化)，该曲线表征了特征值的变化情况。一般来讲，含噪数据的L曲线可明显分为两个部分：对应有效地质成分的特征值幅度较大，衰减较快；而对应噪声成分的特征值幅度要小得多，衰减较慢且数值变化平稳。根据这个特性，很容易确定L曲线的角点位置，如图4(a)中第3个特征值。如果要定量地确定L曲线的角点位置，那么可以先求出相邻两个特征值的斜率，然后依次求出前一斜率和后一斜率的比值，最后确定出最大的斜率比值所对应的特征值，其中斜率比值如图4(b)所示。

由图4(a)可见，第3个特征值之前的曲线幅值较大，变化较快；而其值之后的曲线幅值较小，变化缓慢，所以第3个特征值就是L曲线的角点位置。此外，在图4(b)中，我们也可以发现，具有最大斜率比值所对应的特征值正是第3个特征值。实际上，斜率比值反映了特征值曲线变化率的突变情况。所以应用L曲线法可以定量判别地质成分和噪声成分。因此根据上述方法，我们判定成分1、成分2、成分3代表有效的地质成分，而成分4-成分20主要反映噪声信息。

从上述分析可以看到，分别应用基于L曲线的信噪分离准则和基于曲线趋势对比的分离准则所获得的结果是一致的。重构成分1、成分2、成分3获得的单点衰减曲线如图5所示。从图5中可以看到，噪声得到了较好地抑制。

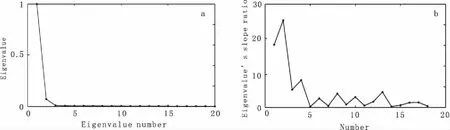
图4 含噪数据的L曲线Fig．4 L curve (a)含噪模拟数据的L曲线；(b)特征值斜率比值

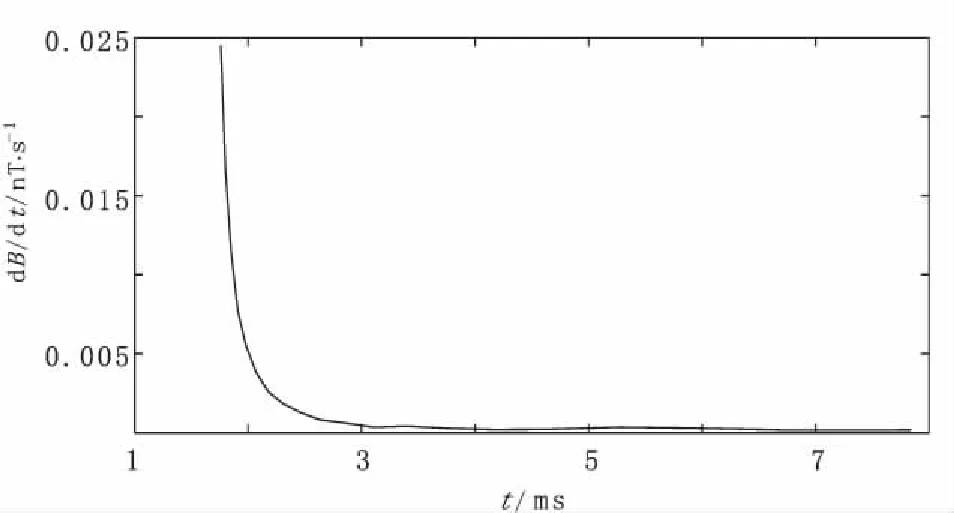
图5 去噪后的电磁响应曲线Fig．5 The attenuation curve of EM response denoised

3.2 实测数据实验

图6为吊舱式直升机时间域电磁测量系统在某一勘探区的实测单点衰减曲线，其中该数据已经进行了叠加、抽道、归一化处理。叠加和抽道主要是为了抑制随机噪声。从图6中，还可以发现，尽管通过叠加抽道可以抑制大部分随机噪声，但是不能有效减弱天电噪声和人文噪声的影响。对图6中的数据应用主成分分析法处理后，获得的去噪结果如图7所示。对比分析图6和图7可以发现，经过主成分分析去噪后衰减曲线变得较为光滑，这说明主成分分析法能有效抑制航空瞬变电磁数据中的天电噪声和人文噪声，且计算较为简单。

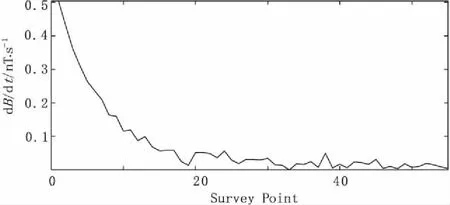
图6 实测电磁响应衰减曲线Fig．6 A raw decay measured

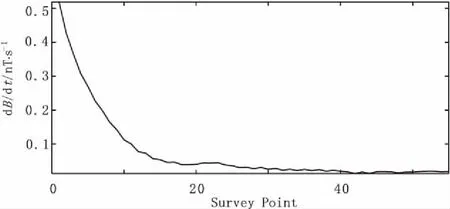
图7 去噪后的电磁响应衰减曲线Fig．7 A denoised decay

4 结论

主成分分析是一种统计分析方法，从统计角度能对有效信号和噪声进行分离。从上述的实验结果及分析可知，主成分分析能有效抑制航空瞬变电磁法中的天电噪声和人文噪声。此外，主成分分析主要包含分解和重构两个部分，在分解时是对整个勘探区的数据进行分解，所获得特征向量比较稳定；而在重构时所要计算的成分大为减少，所以基于主成分的航空瞬变电磁去噪方法不仅算法稳定，而且计算效率较高。

参考文献：

[1] 雷栋, 胡祥云, 张素芳. 航空电磁法发展现状[J]. 地质找矿论丛, 2006, 21(1): 42-44.

[2] MCCRACKEN K G, PIK J P, HARRIS R W. Noise in EM exploration systems[J]. Exploration geophysics, 1984, 15(3): 169-174.

[3] SZARKA L. Geophysical aspects of man-made electromagnetic noise in the earth—review[J]. Surveys in geophysics, 1988, 9(3-4): 287-318.

[4] 陶本藻. 论最小二乘拟合[J]. 武汉大学学报：信息科学版, 1980(1): 27-34.

[5] AL-FOUZAN F, WILLIAM HARBERT, ROBERT DILMORE，et al. Methods for Removing Signal Noise from Helicopter Electromagnetic Survey Data[J]. Mine Water and the Environment, 2004, 23(1): 28-33.

[6] MACNAE J C, LAMONTAGNE Y, WEST G F. Noise processing techniques for time- domain EM systems[J]. Geophysics, 1984, 49(7): 934-948.

[7] SCOTT R, ATKINS F, HARPER P V. Median window filter as a smoothing-edge preserving technique[J]. Journal of nuclear medicine, 1978, 19(6):749.

[8] BUSELLI G, CAMERON M. Robust statistical methods for reducing sferics noise contaminating transient electromagnetic measurements[J]. Geophysics, 1996, 61(6):1633-1646.

[9] 吕东伟, 毛立峰. 时间域航空电磁资料小波去噪方法研究[C]. 第九届中国国际地球物理电磁学术讨论会论文, 2009.

[10] SPIES B R. Local noise prediction filtering for central induction transient electromagnetic sounding[J]. Geophysics, 1988, 53(8): 1068-1079.

[11] OLSEN K B, HOHMANN G W. Adaptive noise cancellation for time-domain EM data[J]. Geophysics, 1992, 57(3):466-469.

[12] DOUGLAS C, NYMAN, JAMES E G, et al. Adaptive rejection of high-line contamination[C]. 1983 SEG annual meeting, 1983.

[13] 夏江海.奇异值分解在位场资料中的应用[J]. 物探化探计算技术, 1989, 11(2): 93-98.

[14] 王权海,苗放.提高地震数据信噪比的PCA方法[J]. 地球物理学进展, 2011, 26 (3): 1039-1044.

[15] RENINGER P A, MARTELET G. Singular value decomposition as a denoising tool for airborne time domain electromagnetic data[J]. Journal of Applied Geophysics, 2011, 75(2) : 264-276.

[16] 黄皓平.电磁法数据处理的奇异值分解法[J]. 地球物理学报, 1991, 34(5): 644-650.

[17] LAWSON C L, HANSON R J. Solving least squares problems[M]. Englewood Cliffs: Prentice-Hall, 1974.

[18] HANSEN P C. Analysis of discrete ill-posed problems by means of the L-curve[J]. SIAM review, 1992, 34(4): 561-580.

[19] HANSEN P C. Regularization, GSVD and truncaed GSVD[J]. BIT numerical mathematics, 1989, 29(3): 491-504.